Population-Based Metaheuristics

CSI 4106 - Fall 2024

Marcel Turcotte

Version: Nov 17, 2024 11:46

Preamble

Quote of the Day

Learning Objectives

  • Understand the definition and purpose of metaheuristics in optimization problems.
  • Learn the principles and components of genetic algorithms (GAs).
  • Comprehend the implementation details of GAs, including encoding, selection, crossover, mutation, and fitness evaluation.
  • Apply GAs to solve the 0/1 knapsack problem with practical Python examples.
  • Recognize different encoding schemes and selection methods in GAs.

Introduction

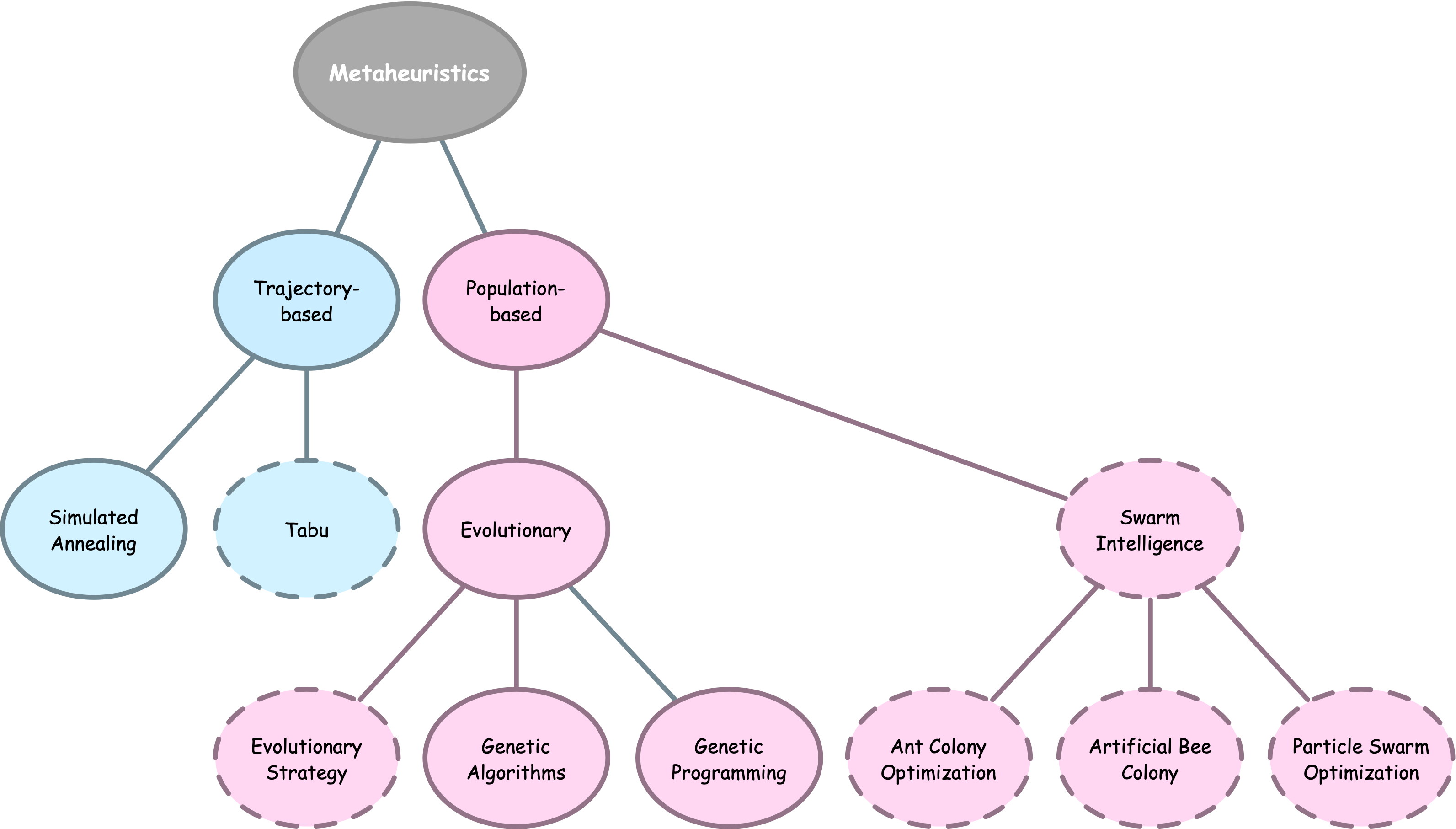
Metaheuristics

Definition

(Gil-Rios et al. 2021)

Metaheuristics are higher-level procedures or heuristics designed to guide the search for solutions in optimization problems with large solution spaces, aiming to find good solutions more efficiently than traditional methods.

Meta heuristics balance exploitation and exploration to avoid local optima, often incorporating randomness, memory, or adaptive mechanisms.

Definition

A genetic algorithm is an evolutionary optimization technique that uses a population of candidate solutions, evolving them through selection, crossover, and mutation to iteratively improve towards an “optimal” solution.

Applications

  • Optimization: Solving complex engineering, logistics, and scheduling problems.
  • Machine Learning: Feature selection, hyperparameter tuning, and evolving neural network architectures.
  • Robotics: Path planning, sensor optimization, control strategy development, and robot designs1.

Applications (continued)

Oliva, Houssein, and Hinojosa (2021)

Springer Link

Eddaly, Jarboui, and Siarry (2023)

Springer Link

From Biology to Genetic Algorithms

(Mayr 1982, 481)

There is probably no more original, more complex, and bolder concept in the history of ideas than Darwin’s mechanistic explanation of adaptation.

(Dennett 1995)

If I were to give an award for the single best idea anyone has ever had, I’d give it to Darwin, ahead of Newton & Einstein and everyone else.

Definition

(Gregory 2009)

Natural selection is a non-random difference in reproductive output among replicating entities, often due indirectly to differences in survival in a particular environment, leading to an increase in the proportion of beneficial, heritable characteristics within a population from one generation to the next.

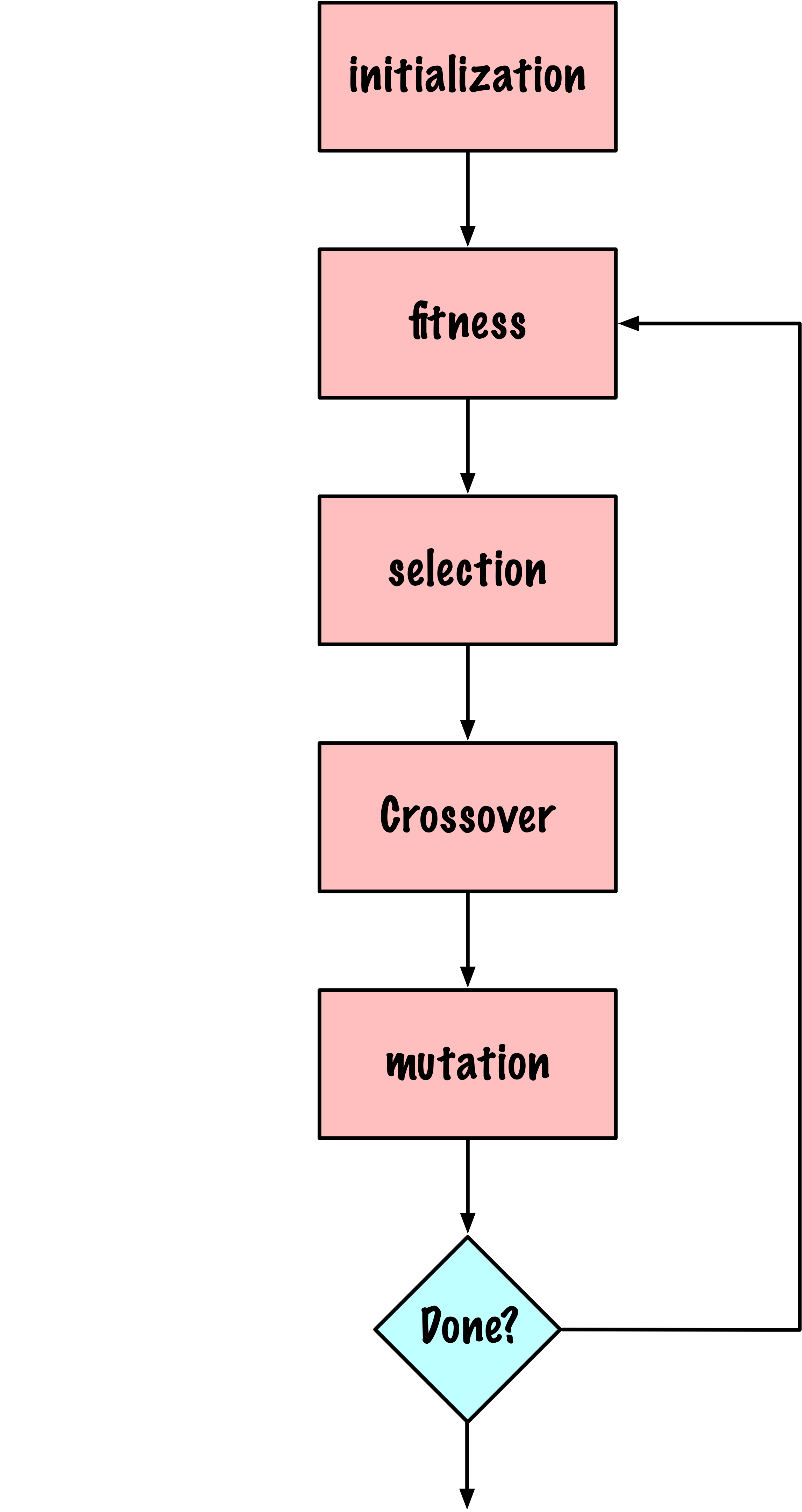
Components

Basic GA

  1. Initialize population
  2. Compute the fitness
  3. Select individuals (chromosomes)
  4. Crossover
  5. Mutation
  6. If not done, goto 2

Choices

  • How to encode a candidate solution or state?
  • How to select candidate solutions?
  • How to define the crossover operator?
  • How to define the mutation operator?
  • How to calculate the fitness?

Problem

0/1 knapsack problem: Given items with defined weights and values, the objective is to maximize total value by selecting items for a knapsack without surpassing a fixed capacity. Each item must be either fully included (1) or excluded (0).

Problem (continued)

\[ \begin{aligned} & \text { maximize } \sum_{i=1}^n x_i \cdot v_i \\ & \text { subject to } \sum_{i=1}^n x_i \cdot w_i \leq W \text { and } x_i \in\{0,1\} . \end{aligned} \]

where \(W\) represents the fixed maximum weight, and \(x_i\) is a binary variable indicating whether item \(i\) is included (1) or excluded (0).

Applications

  1. Finance and Investment: In portfolio optimization, where each asset has a risk (analogous to weight) and expected return (value), the knapsack framework helps select a set of assets that maximizes return without exceeding a risk threshold.

  2. Resource Allocation: Common in project management, where resources (budget, personnel, time) need to be allocated across projects or tasks to maximize overall value, taking into account limited availability.

  3. Supply Chain and Logistics: Used to maximize the value of goods transported within vehicle weight or volume constraints. It can also be applied in warehouse storage, where space is limited, and high-value items are prioritized.

  4. Ad Placement and Marketing: Used in digital advertising to select the most profitable combination of ads to display within limited space (e.g., website or app banner space), maximizing revenue under size or display constraints.

Greedy Algorithms

(Skiena 2008, 192)

Greedy algorithms make the decision of what to do next by selecting the best local option from all available choices without regard to the global structure.

Data

import numpy as np

# Sample data

values = np.array([
    360, 83, 59, 130, 431, 67, 230, 52, 93, 125, 670, 892, 600, 38, 48, 147,
    78, 256, 63, 17, 120, 164, 432, 35, 92, 110, 22, 42, 50, 323, 514, 28,
    87, 73, 78, 15, 26, 78, 210, 36, 85, 189, 274, 43, 33, 10, 19, 389, 276,
    312])

weights = np.array([
    7, 0, 30, 22, 80, 94, 11, 81, 70, 64, 59, 18, 0, 36, 3, 8, 15, 42, 9, 0,
    42, 47, 52, 32, 26, 48, 55, 6, 29, 84, 2, 4, 18, 56, 7, 29, 93, 44, 71,
    3, 86, 66, 31, 65, 0, 79, 20, 65, 52, 13])

capacity = 850

Ascending order of weight

def greedy_knapsack_weight(weights, values, capacity):

    num_items = len(weights)

    # Create a list of items with their values and original indices
    items = list(zip(weights, values, range(num_items)))

    # Sort items by weight in increasing order
    items.sort()
    
    total_weight, total_value = 0,0
    solution = np.zeros(num_items, dtype=int)
    
    # Select items based on the sorted order
    for w, v, idx in items:
        if total_weight + w <= capacity:
            solution[idx] = 1
            total_weight += w
            total_value += v
        else:
            break  # Skip items that would exceed the capacity
    
    return solution, total_value, total_weight

greedy_knapsack_weight

solution, total_value, total_weight = greedy_knapsack_weight(weights, values, capacity)

print(f"Solution: {solution}")
print(f"Value: {total_value}")
print(f"Weight: {total_weight}")
Solution: [1 1 1 1 0 0 1 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 1 1 1 1 1 1 0
 1 0 1 0 0 1 0 1 0 1 0 1 1]
Value: 5891
Weight: 817

Descending value order

def greedy_knapsack_value(weights, values, capacity):

    num_items = len(weights)

    # Create a list of items with their values and original indices
    items = list(zip(values, weights, range(num_items)))

    # Sort items by value in decreasing order
    items.sort(reverse=True)
    
    total_weight = 0
    total_value = 0
    solution = np.zeros(num_items, dtype=int)
    
    # Select items based on the sorted order
    for v, w, idx in items:
        if total_weight + w <= capacity:
            solution[idx] = 1
            total_weight += w
            total_value += v
    
    return solution, total_value, total_weight

greedy_knapsack_value

solution, total_value, total_weight = greedy_knapsack_value(weights, values, capacity)

print(f"Solution: {solution}")
print(f"Value: {total_value}")
print(f"Weight: {total_weight}")
Solution: [1 1 0 1 1 0 1 0 0 1 1 1 1 0 1 1 0 1 0 1 1 1 1 0 0 0 0 0 0 1 1 0 0 0 1 0 0
 0 1 1 0 1 1 0 1 0 0 1 1 1]
Value: 7339
Weight: 849

GA Implementation

Encoding

Population

def initialize_population(pop_size, num_items):

    """
    Initialize the population with random binary strings.

    Args:
        pop_size (int): Number of individuals in the population.
        num_items (int): Number of items in the knapsack problem.

    Returns:
        np.ndarray: Initialized population.
    """

    return np.random.randint(2, size=(pop_size, num_items))

Population

The proposed method for initializing the population presents a problem.

Fitness

def evaluate_fitness(population, weights, values, capacity, penalty_factor=10):

    total_weights = np.dot(population, weights)

    total_values = np.dot(population, values)

    penalties = penalty_factor * np.maximum(0, total_weights - capacity)

    fitness = total_values - penalties

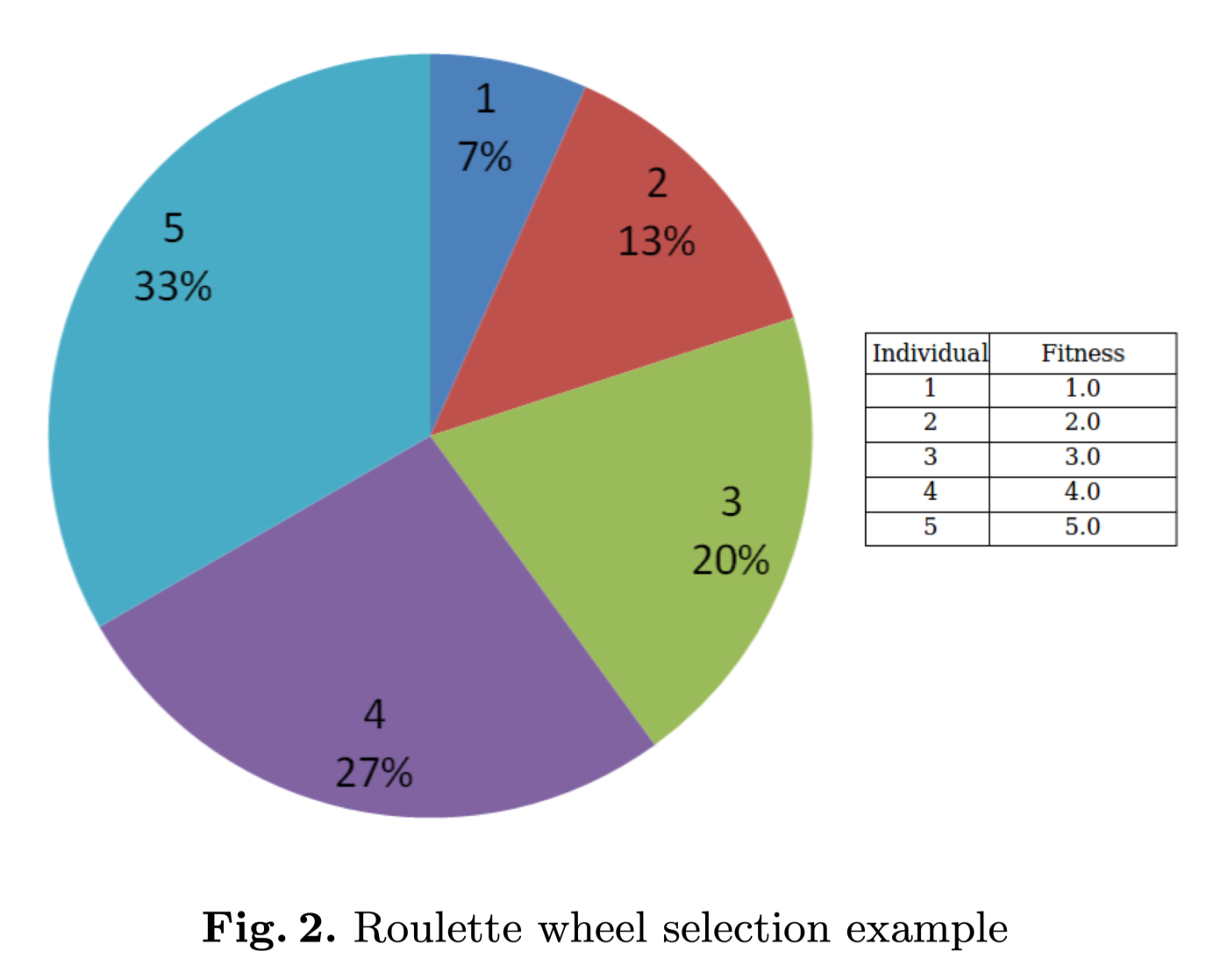
    return fitness

Roulette Wheel Selection

Roulette wheel selection is a stochastic selection method where the probability of selecting an individual is proportional to its fitness relative to the rest of the population.

roulette_selection

def roulette_selection(population, fitness):

    # Adjust fitness to be non-negative
    min_fitness = np.min(fitness)
    adjusted_fitness = fitness - min_fitness + 1e-6  # small epsilon to avoid zero division

    total_fitness = np.sum(adjusted_fitness)
    probabilities = adjusted_fitness / total_fitness

    pop_size = population.shape[0]
    selected_indices = np.random.choice(pop_size, size=pop_size, p=probabilities)

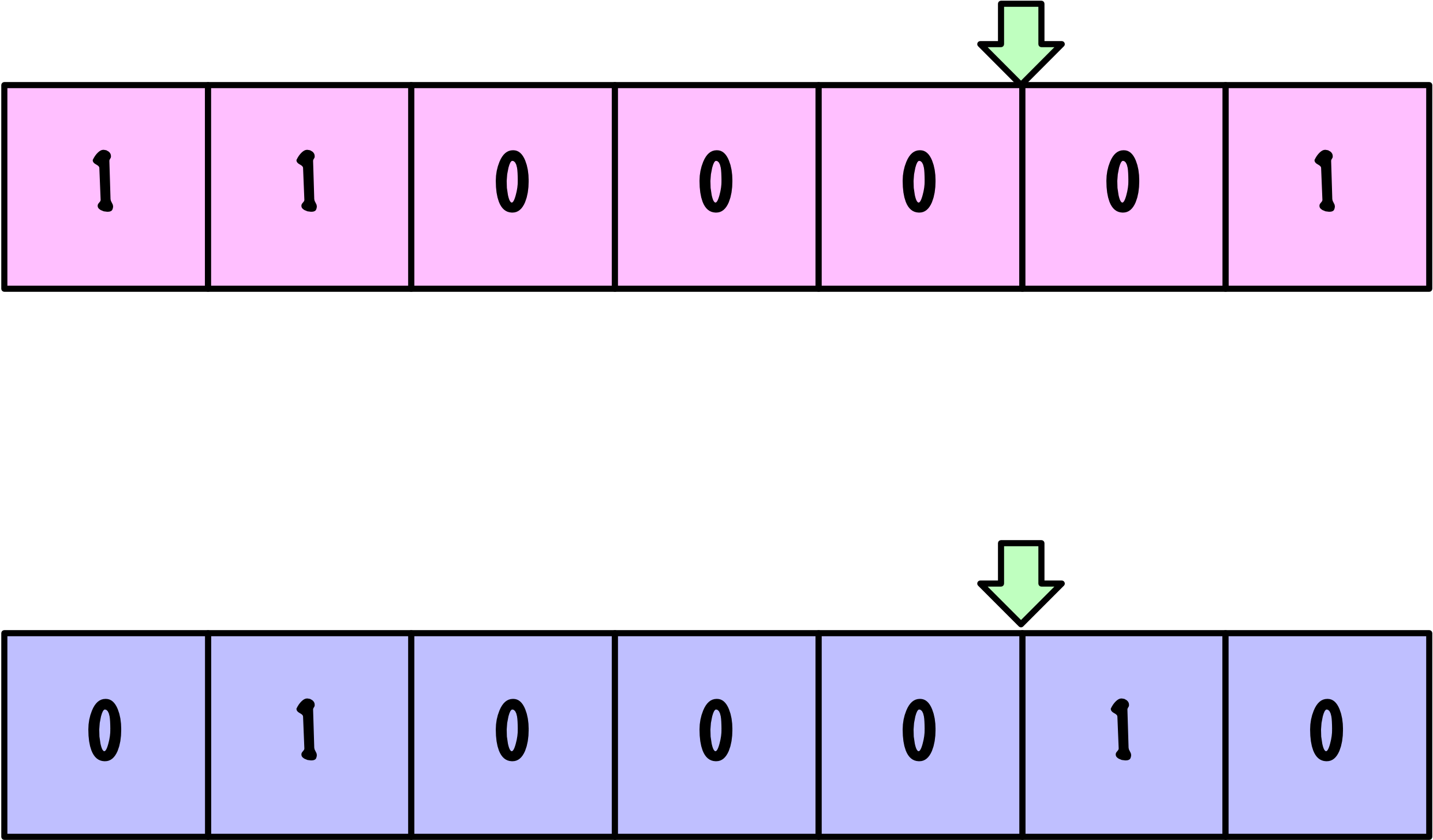
    return population[selected_indices]

Crossover

Crossover

Parents

Offspring

Crossover

def single_point_crossover(parents, crossover_rate):

    num_parents, num_genes = parents.shape
    np.random.shuffle(parents)
    offspring = []

    for i in range(0, num_parents, 2):

        parent1 = parents[i]
        parent2 = parents[i+1 if i+1 < num_parents else 0]

        child1 = parent1.copy()
        child2 = parent2.copy()

        if np.random.rand() < crossover_rate:
            point = np.random.randint(1, num_genes)  # Crossover point
            child1[:point], child2[:point] = parent2[:point], parent1[:point]

        offspring.append(child1)
        offspring.append(child2)

    return np.array(offspring)

Mutation

Mutate

def mutation(offspring, mutation_rate):

    num_offspring, num_genes = offspring.shape

    mutation_matrix = np.random.rand(num_offspring, num_genes) < mutation_rate

    offspring[mutation_matrix] = 1 - offspring[mutation_matrix]

    return offspring

Clarification

np.random.seed(42)

offspring = initialize_population(4, 10)

num_offspring, num_genes = offspring.shape

print("Offspring:")
print(offspring)
Offspring:
[[0 1 0 0 0 1 0 0 0 1]
 [0 0 0 0 1 0 1 1 1 0]
 [1 0 1 1 1 1 1 1 1 1]
 [0 0 1 1 1 0 1 0 0 0]]
mutation_rate = 0.05
mutation_matrix = np.random.rand(num_offspring, num_genes) < mutation_rate

print("Mutation matrix:")
print(mutation_matrix)
Mutation matrix:
[[False False False False False False False False False  True]
 [False False False False False False False False False False]
 [False False  True False False False False False False False]
 [False False False False False False False False  True False]]
print("offspring[mutation_matrix]:")
print(offspring[mutation_matrix])
offspring[mutation_matrix]:
[1 1 0]
print("1 - offspring[mutation_matrix]:")
print(1 - offspring[mutation_matrix])
1 - offspring[mutation_matrix]:
[0 0 1]
offspring[mutation_matrix] = 1 - offspring[mutation_matrix]

print("Mutated offstring:")
print(offspring)
Mutated offstring:
[[0 1 0 0 0 1 0 0 0 0]
 [0 0 0 0 1 0 1 1 1 0]
 [1 0 0 1 1 1 1 1 1 1]
 [0 0 1 1 1 0 1 0 1 0]]

Elitism

Elitism in genetic algorithms is a strategy where a subset of the fittest individuals from the current generation is directly carried over to the next generation.

This approach ensures that the best solutions are preserved throughout the evolutionary process, enhancing convergence speed and maintaining high-quality solutions within the population.

Elitism

def elitism(population, fitness, elite_size):

    elite_indices = np.argsort(fitness)[-elite_size:]  # Get indices of top individuals

    elites = population[elite_indices]

    return elites

Genetic Algorithm (Version 1)

def genetic_algorithm(weights, values, capacity, pop_size=100, 
                      num_generations=100, crossover_rate=0.8,
                      mutation_rate=0.05, elite_percent=0.02):

    num_items = len(weights)
    elite_size = max(1, int(pop_size * elite_percent))
    population = initialize_population(pop_size, num_items)

    for generation in range(num_generations):

        fitness = evaluate_fitness(population, weights, values, capacity)

        # Elitism
        elites = elitism(population, fitness, elite_size)

        # Selection
        parents = roulette_selection(population, fitness)

        # Crossover
        offspring = single_point_crossover(parents, crossover_rate)

        # Mutation
        offspring = mutation(offspring, mutation_rate)

        # Create new population
        population = np.vstack((elites, offspring))

        # Ensure population size
        if population.shape[0] > pop_size:
            population = population[:pop_size]
        elif population.shape[0] < pop_size:
            # Add random individuals to fill population
            num_new_individuals = pop_size - population.shape[0]
            new_individuals = initialize_population(num_new_individuals, num_items)
            population = np.vstack((population, new_individuals))

    # After all generations, return the best solution
    fitness = evaluate_fitness(population, weights, values, capacity)
    best_index = np.argmax(fitness)
    best_solution = population[best_index]
    best_value = np.dot(best_solution, values)
    best_weight = np.dot(best_solution, weights)

    return best_solution, best_value, best_weight

Run

np.random.seed(13)

solution, total_value, total_weight = genetic_algorithm(weights, values, capacity)

print(f"Solution: {solution}")
print(f"Value: {total_value}")
print(f"Weight: {total_weight}")
Solution: [1 1 0 1 1 0 1 0 0 0 1 1 1 0 1 1 1 1 1 0 1 1 1 0 0 1 0 1 0 1 1 1 1 1 1 0 0
 1 0 1 0 0 1 0 1 0 0 1 1 1]
Value: 7357
Weight: 848

Genetic Algorithm (Version 1.1)

def genetic_algorithm(weights, values, capacity, pop_size=100, 
                      num_generations=100, crossover_rate=0.8, 
                      mutation_rate=0.05, elite_percent=0.02):

    num_items = len(weights)
    elite_size = max(1, int(pop_size * elite_percent))
    population = initialize_population(pop_size, num_items)

    average_fitness_history = []
    best_fitness_history = []

    for generation in range(num_generations):

        fitness = evaluate_fitness(population, weights, values, capacity)

        # Track average and best fitness
        average_fitness = np.mean(fitness)
        best_fitness = np.max(fitness)
        average_fitness_history.append(average_fitness)
        best_fitness_history.append(best_fitness)

        # Elitism
        elites = elitism(population, fitness, elite_size)

        # Selection
        parents = roulette_selection(population, fitness)

        # Crossover
        offspring = single_point_crossover(parents, crossover_rate)

        # Mutation
        offspring = mutation(offspring, mutation_rate)

        # Create new population
        population = np.vstack((elites, offspring))

        # Ensure population size
        if population.shape[0] > pop_size:
            population = population[:pop_size]
        elif population.shape[0] < pop_size:
            # Add random individuals to fill population
            num_new_individuals = pop_size - population.shape[0]
            new_individuals = initialize_population(num_new_individuals, num_items)
            population = np.vstack((population, new_individuals))

    # After all generations, return the best solution
    fitness = evaluate_fitness(population, weights, values, capacity)
    best_index = np.argmax(fitness)
    best_solution = population[best_index]
    best_value = np.dot(best_solution, values)
    best_weight = np.dot(best_solution, weights)

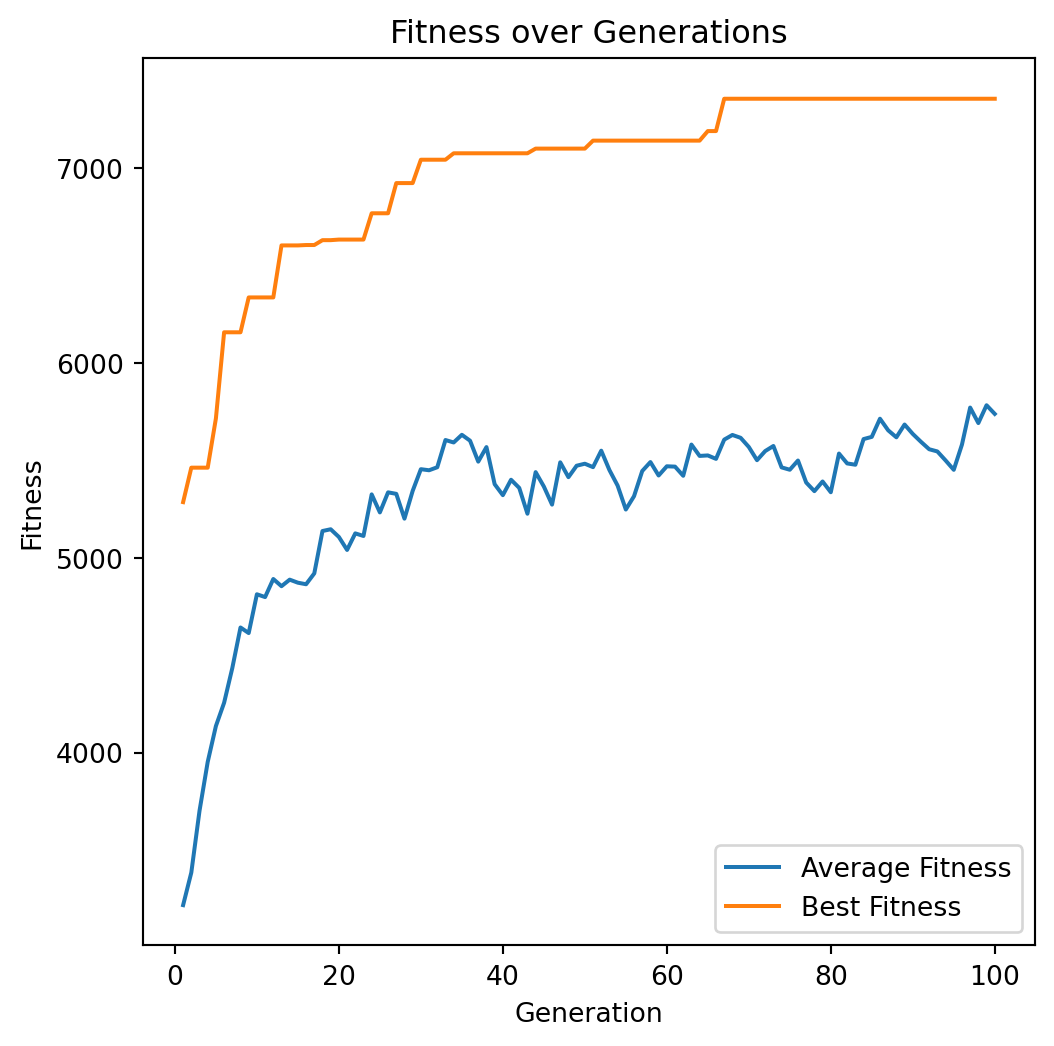
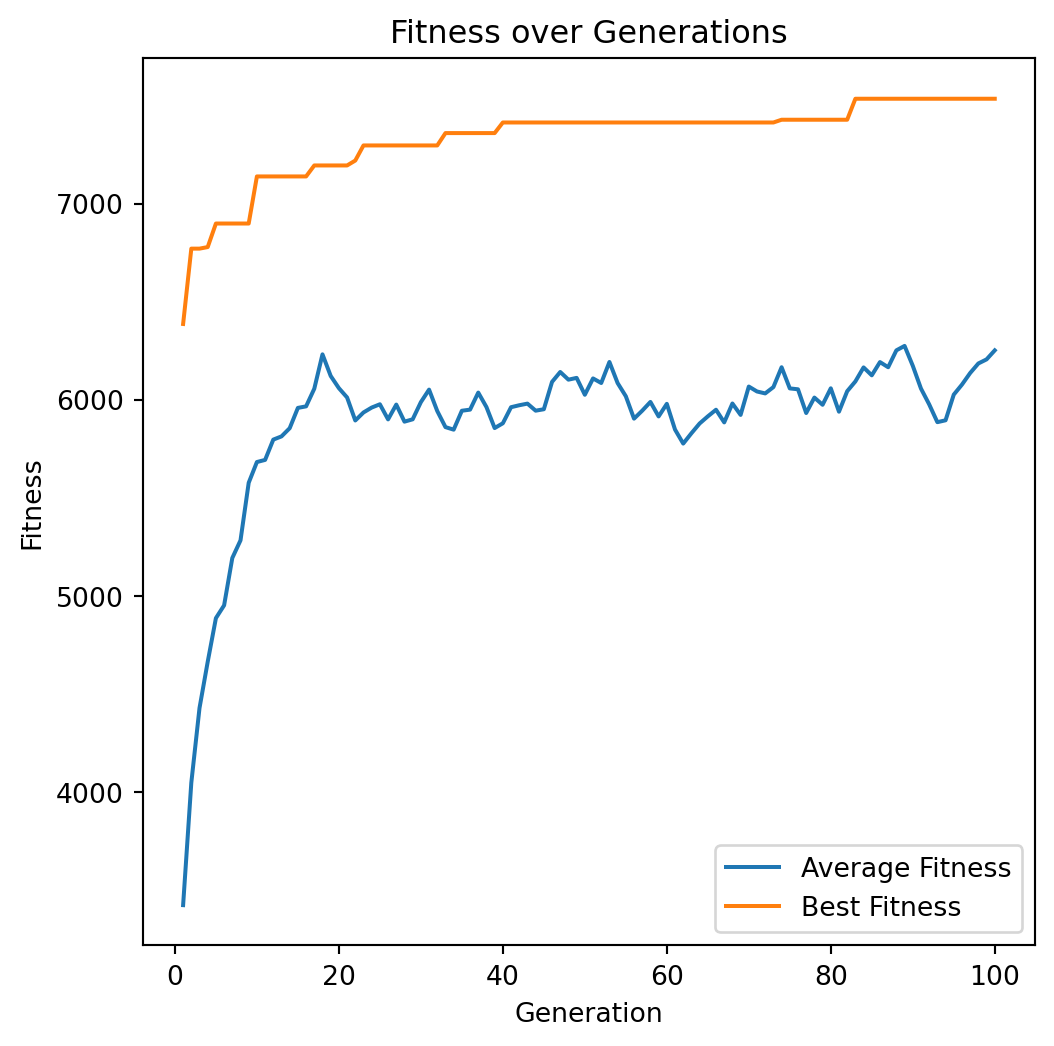
    return best_solution, best_value, best_weight, average_fitness_history, best_fitness_history

Plot

import matplotlib.pyplot as plt

def plot_fitness_over_generations(avg_fitness_history, best_fitness_history):

  generations = range(1, len(avg_fitness_history) + 1)

  plt.figure(figsize=(6, 6))

  plt.plot(generations, avg_fitness_history, label='Average Fitness')
  plt.plot(generations, best_fitness_history, label='Best Fitness')
  plt.xlabel('Generation')
  plt.ylabel('Fitness')
  plt.title('Fitness over Generations')
  plt.legend()

Run

np.random.seed(13)

solution, total_value, total_weight, avg_fitness_history, best_fitness_history = genetic_algorithm(weights, values, capacity)

print(f"Solution: {solution}")
print(f"Value: {total_value}")
print(f"Weight: {total_weight}")

plot_fitness_over_generations(avg_fitness_history, best_fitness_history)

Run

Solution: [1 1 0 1 1 0 1 0 0 0 1 1 1 0 1 1 1 1 1 0 1 1 1 0 0 1 0 1 0 1 1 1 1 1 1 0 0
 1 0 1 0 0 1 0 1 0 0 1 1 1]
Value: 7357
Weight: 848

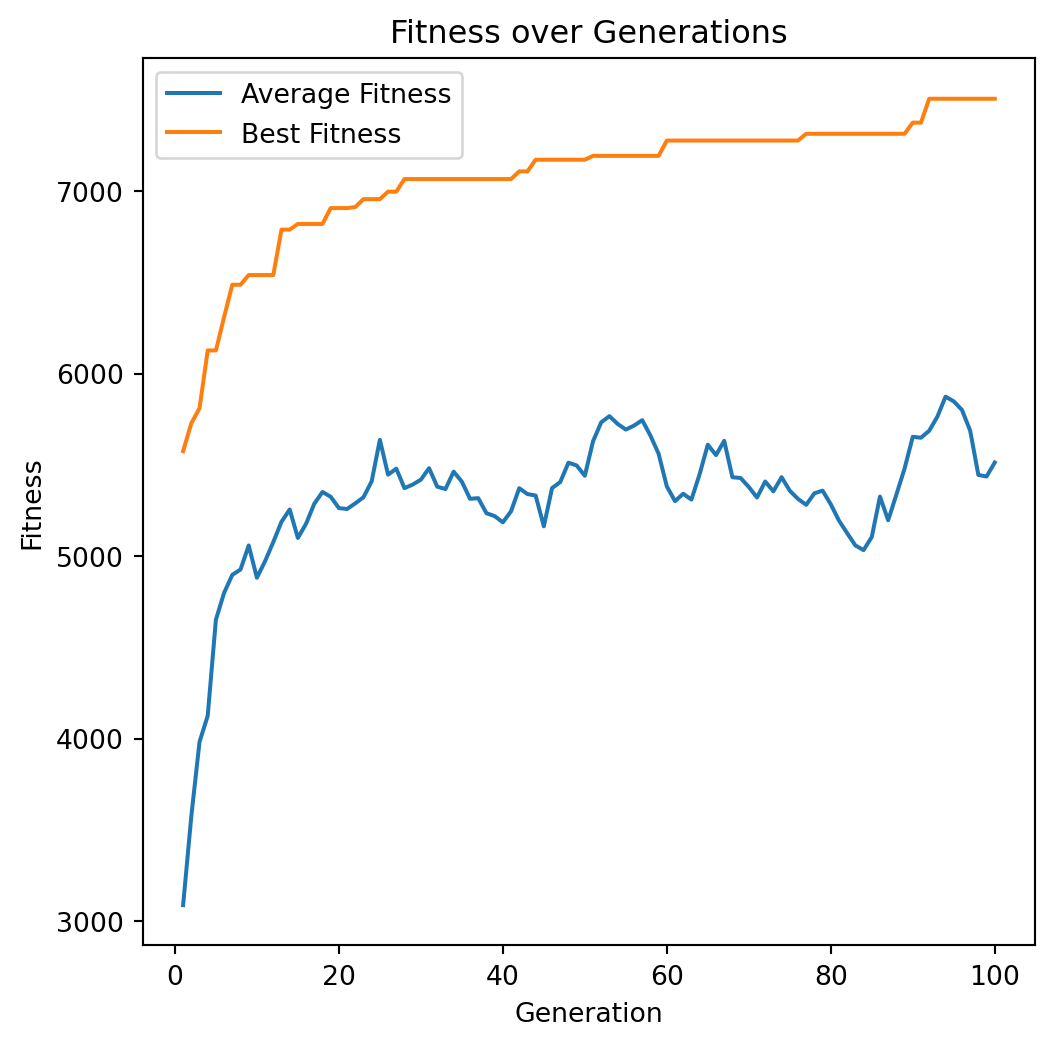
Run

np.random.seed(42)

best_value = -1
best_weight = -1
best_solution, best_averages, best_bests = None,  None, None

for i in range(100):

  solution, total_value, total_weight, avg_fitness_history, best_fitness_history = genetic_algorithm(weights, values, capacity)

  if total_value > best_value and total_weight <= capacity:
    best_value = total_value
    best_weight = total_weight
    best_solution = solution
    best_averages = avg_fitness_history
    best_bests = best_fitness_history


print(f"Solution: {best_solution}")
print(f"Value: {best_value}")
print(f"Weight: {best_weight}")

plot_fitness_over_generations(best_averages, best_bests)

Run

Solution: [1 1 0 1 1 0 1 0 0 0 1 1 1 0 1 1 1 1 1 1 0 1 1 0 1 0 0 1 1 1 1 0 1 0 1 0 0
 0 1 1 0 1 1 0 1 0 0 1 1 1]
Value: 7506
Weight: 846

Using Google OR Tools

# https://developers.google.com/optimization/pack/knapsack

from ortools.algorithms.python import knapsack_solver

def solve_using_ortools(values, weights, capacity):

  weights = [weights]

  # Create the solver
  
  solver = knapsack_solver.KnapsackSolver(
      knapsack_solver.SolverType.KNAPSACK_MULTIDIMENSION_BRANCH_AND_BOUND_SOLVER,
      "KnapsackExample",
  )

  solver.init(values, weights, [capacity])

  computed_value = solver.solve()

  packed_items = []
  packed_weights = []
  total_weight = 0
  print("Total value =", computed_value)
  for i in range(len(values)):
      if solver.best_solution_contains(i):
          packed_items.append(i)
          packed_weights.append(weights[0][i])
          total_weight += weights[0][i]
  print("Total weight:", total_weight)
  print("Packed items:", packed_items)
  print("Packed_weights:", packed_weights)

solve_using_ortools

solve_using_ortools(values, weights, capacity)
Total value = 7534
Total weight: 850
Packed items: [0, 1, 3, 4, 6, 10, 11, 12, 14, 15, 16, 17, 18, 19, 21, 22, 24, 27, 28, 29, 30, 31, 32, 34, 38, 39, 41, 42, 44, 47, 48, 49]
Packed_weights: [7, 0, 22, 80, 11, 59, 18, 0, 3, 8, 15, 42, 9, 0, 47, 52, 26, 6, 29, 84, 2, 4, 18, 7, 71, 3, 66, 31, 0, 65, 52, 13]

Discussion

Encoding Schemes

  • Binary encoding is commonly used.

  • Permutation encoding. Typically used with problems such as “Travelling Salesman Problem (TSP)” and N-Queens.

  • Values encoding. In this encoding, integer, real, or character values are used. Example: learning the parameters of a polynomical in a regression problem.

Selection

Tournament selection involves randomly selecting a subset of individuals (a tournament) from the population and then selecting the best individual from this subset to be a parent. The process is repeated until the required number of parents is selected.

This method balances between exploration and exploitation. It allows for controlling selection pressure by varying the tournament size. Larger tournaments increase selection pressure, favoring the fittest individuals more strongly.

tournament_selection

def tournament_selection(population, fitness, tournament_size):

    pop_size = population.shape[0]

    selected_indices = []

    for _ in range(pop_size):

        participants = np.random.choice(pop_size, tournament_size, replace=False)

        best = participants[np.argmax(fitness[participants])]

        selected_indices.append(best)

    return population[selected_indices]

Discussion

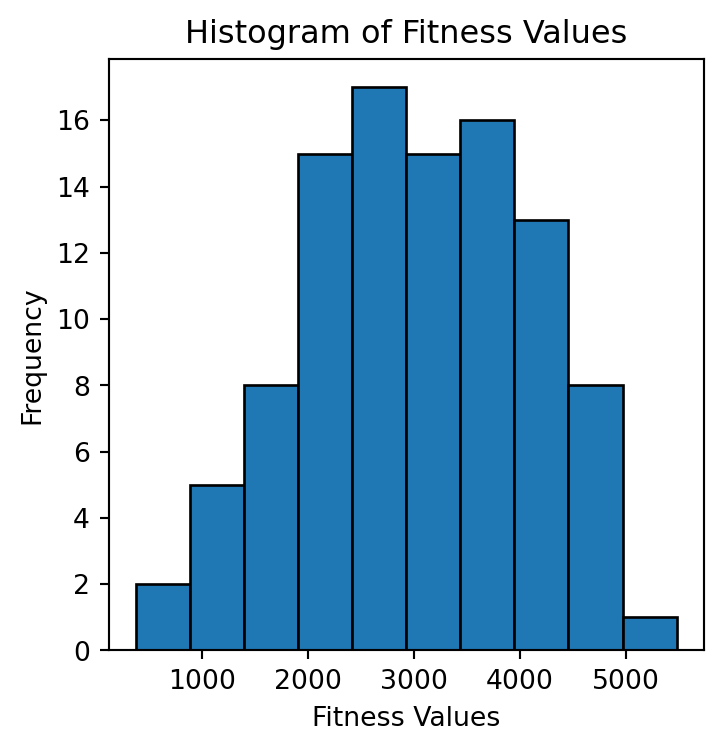
np.random.seed(27)

pop_size, num_items = 100, 50

population = initialize_population(pop_size, num_items)

fitness = evaluate_fitness(population, weights, values, capacity)

plt.figure(figsize=(4, 4))
plt.hist(fitness, bins=10, edgecolor='black')
plt.xlabel('Fitness Values')
plt.ylabel('Frequency')
plt.title('Histogram of Fitness Values')
plt.show()

for tournament_size in [2, 4, 8, pop_size]:
  participants = np.random.choice(pop_size, tournament_size, replace=False)
  print(f"tournament_size: {tournament_size}, fitness: {max(fitness[participants])}")

Discussion

tournament_size: 2, fitness: 1985
tournament_size: 4, fitness: 2933
tournament_size: 8, fitness: 3966
tournament_size: 100, fitness: 5478

Genetic Algorithm (Version 2)

def genetic_algorithm(weights, values, capacity, pop_size=100, 
                      num_generations=100, crossover_rate=0.8,
                      mutation_rate=0.05, elite_percent=0.02, 
                      selection_type='tournament', tournament_size=3):

    num_items = len(weights)
    elite_size = max(1, int(pop_size * elite_percent))
    population = initialize_population(pop_size, num_items)

    average_fitness_history = []
    best_fitness_history = []

    for generation in range(num_generations):

        fitness = evaluate_fitness(population, weights, values, capacity)

        # Track average and best fitness
        average_fitness = np.mean(fitness)
        best_fitness = np.max(fitness)
        average_fitness_history.append(average_fitness)
        best_fitness_history.append(best_fitness)

        # Elitism
        elites = elitism(population, fitness, elite_size)

        # Selection
        if selection_type == 'tournament':
            parents = tournament_selection(population, fitness, tournament_size)
        elif selection_type == 'roulette':
            parents = roulette_selection(population, fitness)
        else:
            raise ValueError("Invalid selection type")

        # Crossover
        offspring = single_point_crossover(parents, crossover_rate)

        # Mutation
        offspring = mutation(offspring, mutation_rate)

        # Create new population
        population = np.vstack((elites, offspring))

        # Ensure population size
        if population.shape[0] > pop_size:
            population = population[:pop_size]
        elif population.shape[0] < pop_size:
            # Add random individuals to fill population
            num_new_individuals = pop_size - population.shape[0]
            new_individuals = initialize_population(num_new_individuals, num_items)
            population = np.vstack((population, new_individuals))

    # After all generations, return the best solution
    fitness = evaluate_fitness(population, weights, values, capacity)
    best_index = np.argmax(fitness)
    best_solution = population[best_index]
    best_value = np.dot(best_solution, values)
    best_weight = np.dot(best_solution, weights)

    return best_solution, best_value, best_weight, average_fitness_history, best_fitness_history

Run

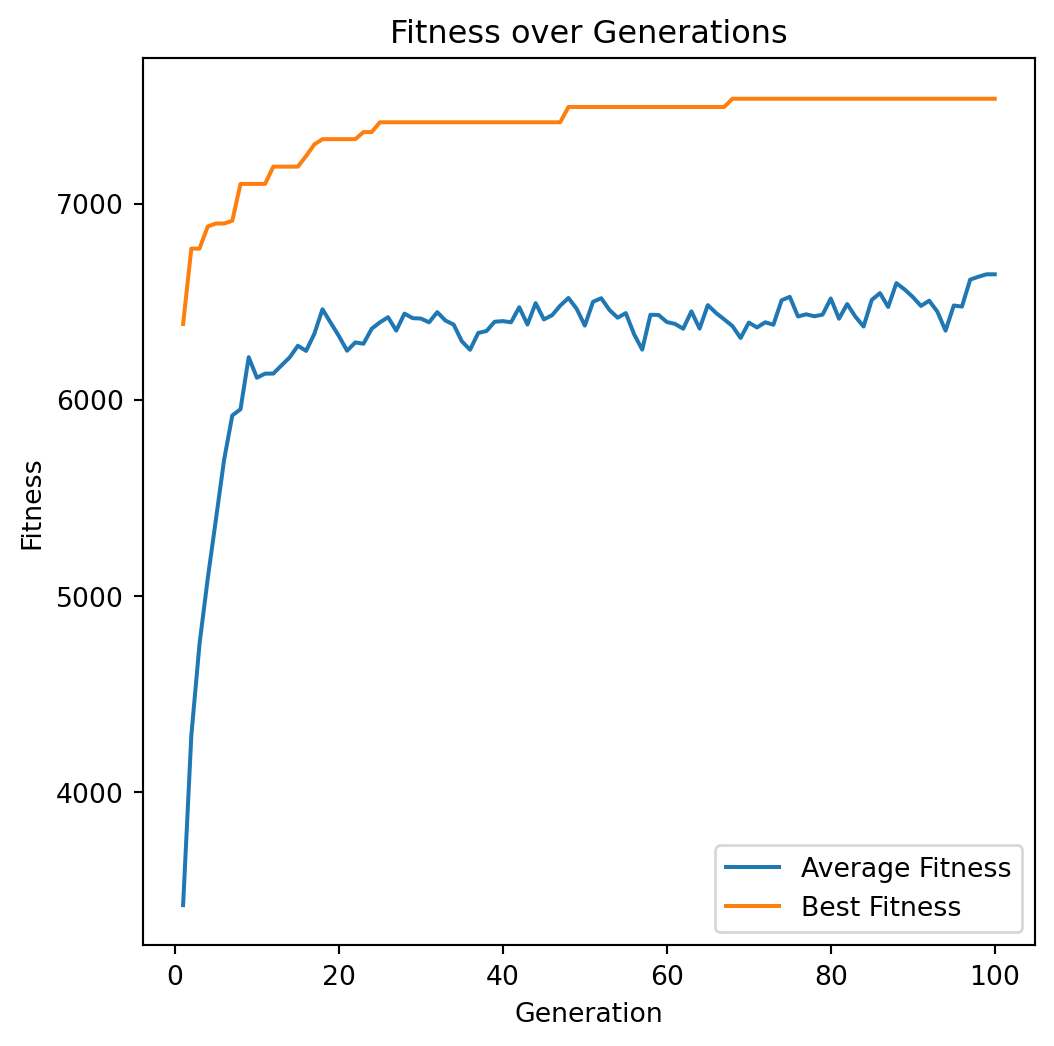
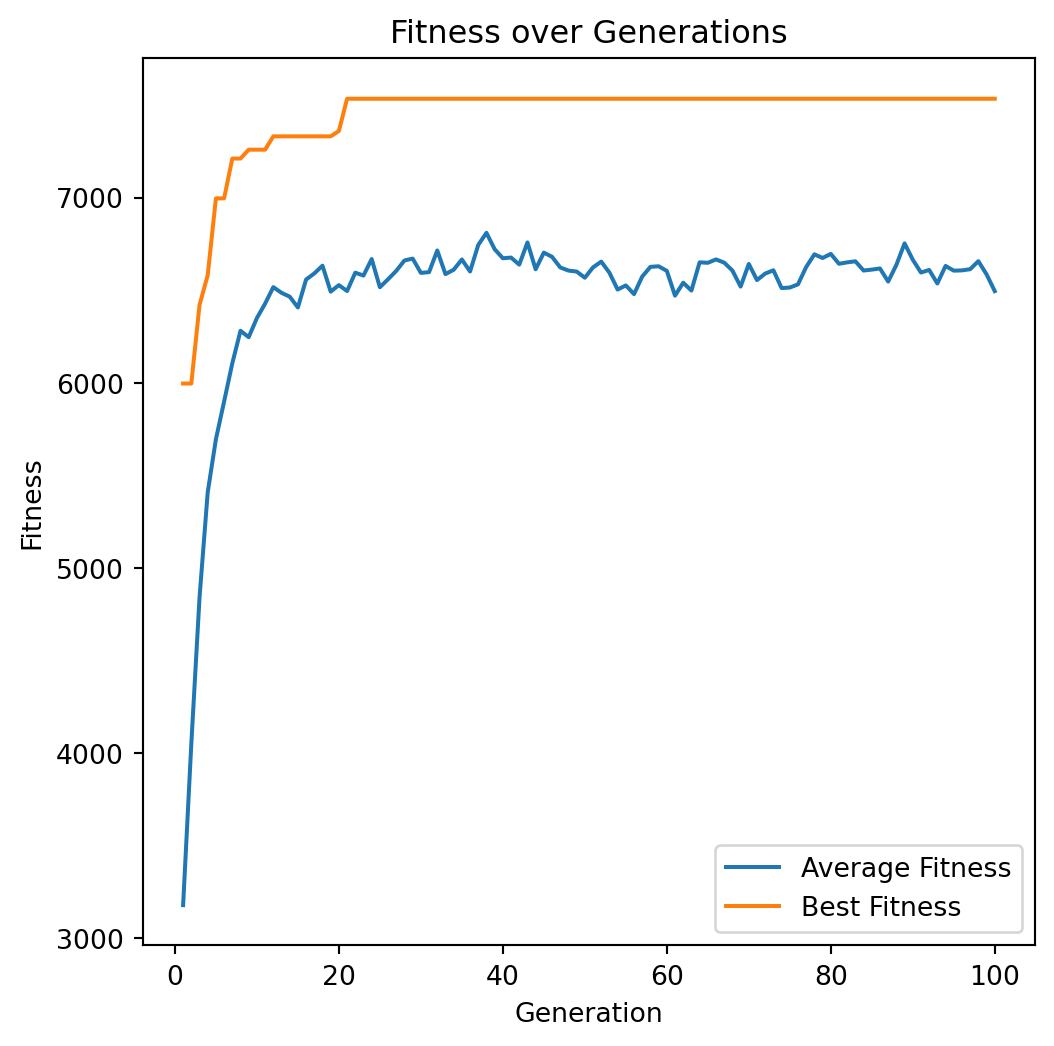
np.random.seed(42)

best_value, best_weight = -1, -1
best_solution, best_averages, best_bests = None,  None, None

for i in range(100):

  solution, total_value, total_weight, avg_fitness_history, best_fitness_history = genetic_algorithm(weights, values, capacity)

  if total_value > best_value and total_weight <= capacity:
    best_value = total_value
    best_weight = total_weight
    best_solution = solution
    best_averages = avg_fitness_history
    best_bests = best_fitness_history


print(f"Solution: {best_solution}")
print(f"Value: {best_value}")
print(f"Weight: {best_weight}")

plot_fitness_over_generations(best_averages, best_bests)

Run

Solution: [1 1 0 1 1 0 1 0 0 0 1 1 1 0 1 1 1 1 1 1 0 1 1 0 1 0 0 1 1 1 1 1 1 0 1 0 0
 0 1 1 0 1 1 0 1 0 0 1 1 1]
Value: 7534
Weight: 850

tournament_size=2, 4, 8

np.random.seed(42)

for tournament_size in (2, 4, 8):

  best_value, best_weight = -1, -1
  best_solution, best_averages, best_bests = None,  None, None

  for i in range(100):

      solution, total_value, total_weight, avg_fitness_history, best_fitness_history = genetic_algorithm(
        weights, values, capacity, tournament_size=tournament_size
      )

      if total_value > best_value and total_weight <= capacity:
        best_value = total_value
        best_weight = total_weight
        best_solution = solution
        best_averages = avg_fitness_history
        best_bests = best_fitness_history

  print(f"Solution: {best_solution}")
  print(f"Value: {best_value}")
  print(f"Weight: {best_weight}")

  plot_fitness_over_generations(best_averages, best_bests)

tournament_size=2, 4, 8

Solution: [1 1 0 1 1 0 1 0 0 0 1 1 1 0 1 1 1 1 1 1 0 1 1 0 1 0 0 1 1 1 1 1 1 0 1 0 0
 0 1 1 0 1 1 0 1 0 0 1 1 1]
Value: 7534
Weight: 850
Solution: [1 1 0 1 1 0 1 0 0 0 1 1 1 0 1 1 1 1 1 1 0 1 1 0 1 0 0 1 1 1 1 1 1 0 1 0 0
 0 1 1 0 1 1 0 1 0 0 1 1 1]
Value: 7534
Weight: 850
Solution: [1 1 0 1 1 0 1 0 0 0 1 1 1 0 1 1 1 1 1 1 0 1 1 0 1 0 0 1 1 1 1 1 1 0 1 0 0
 0 1 1 0 1 1 0 1 0 0 1 1 1]
Value: 7534
Weight: 850

Crossover

  • Single or k-point cross-over.

Uniform crossover

Uniform crossover in genetic algorithms is a recombination technique where each gene in the offspring is independently chosen from one of the two parent genomes with equal probability. This approach allows for a more varied combination of parental traits compared to traditional crossover methods, promoting greater genetic diversity in the resulting population.

uniform_crossover

def uniform_crossover(parents, crossover_rate):

    num_parents, num_genes = parents.shape
    np.random.shuffle(parents)

    offspring = []

    for i in range(0, num_parents, 2):

        parent1 = parents[i]
        parent2 = parents[i+1 if i+1 < num_parents else 0]

        child1 = parent1.copy()
        child2 = parent2.copy()

        if np.random.rand() < crossover_rate:

            mask = np.random.randint(0, 2, size=num_genes).astype(bool)

            child1[mask], child2[mask] = parent2[mask], parent1[mask]

        offspring.append(child1)
        offspring.append(child2)

    return np.array(offspring)

Genetic Algorithm (Version 3)

def genetic_algorithm(weights, values, capacity, pop_size=100, 
                      num_generations=200, crossover_rate=0.8,
                      mutation_rate=0.05, elite_percent=0.02, 
                      selection_type='tournament', tournament_size=3,
                      crossover_type='single_point'):

    num_items = len(weights)
    elite_size = max(1, int(pop_size * elite_percent))
    population = initialize_population(pop_size, num_items)

    average_fitness_history = []
    best_fitness_history = []

    for generation in range(num_generations):

        fitness = evaluate_fitness(population, weights, values, capacity)

        # Track average and best fitness
        average_fitness = np.mean(fitness)
        best_fitness = np.max(fitness)
        average_fitness_history.append(average_fitness)
        best_fitness_history.append(best_fitness)

        # Elitism
        elites = elitism(population, fitness, elite_size)

        # Selection
        if selection_type == 'tournament':
            parents = tournament_selection(population, fitness, tournament_size)
        elif selection_type == 'roulette':
            parents = roulette_selection(population, fitness)
        else:
            raise ValueError("Invalid selection type")

        # Crossover
        if crossover_type == 'single_point':
            offspring = single_point_crossover(parents, crossover_rate)
        elif crossover_type == 'uniform':
            offspring = uniform_crossover(parents, crossover_rate)
        else:
            raise ValueError("Invalid crossover type")

        # Mutation
        offspring = mutation(offspring, mutation_rate)

        # Create new population
        population = np.vstack((elites, offspring))

        # Ensure population size
        if population.shape[0] > pop_size:
            population = population[:pop_size]
        elif population.shape[0] < pop_size:
            # Add random individuals to fill population
            num_new_individuals = pop_size - population.shape[0]
            new_individuals = initialize_population(num_new_individuals, num_items)
            population = np.vstack((population, new_individuals))

    # After all generations, return the best solution
    fitness = evaluate_fitness(population, weights, values, capacity)
    best_index = np.argmax(fitness)
    best_solution = population[best_index]
    best_value = np.dot(best_solution, values)
    best_weight = np.dot(best_solution, weights)

    return best_solution, best_value, best_weight, average_fitness_history, best_fitness_history

Run

np.random.seed(42)

best_value, best_weight = -1, -1
best_solution, best_averages, best_bests = None,  None, None

for i in range(100):

  solution, total_value, total_weight, avg_fitness_history, best_fitness_history = genetic_algorithm(
    weights, values, capacity, crossover_type='uniform'
  )

  if total_value > best_value and total_weight <= capacity:
    best_value = total_value
    best_weight = total_weight
    best_solution = solution
    best_averages = avg_fitness_history
    best_bests = best_fitness_history


print(f"Solution: {best_solution}")
print(f"Value: {best_value}")
print(f"Weight: {best_weight}")

plot_fitness_over_generations(best_averages, best_bests)

Run

Solution: [1 1 0 1 1 0 1 0 0 0 1 1 1 0 1 1 1 1 1 1 0 1 1 0 1 0 0 1 1 1 1 1 1 0 1 0 0
 0 1 1 0 1 1 0 1 0 0 1 1 1]
Value: 7534
Weight: 850

Crossover

Single-Point Crossover is advantageous when building blocks (contiguous gene sequences) are meaningful and beneficial to preserve. However, in the 0/1 Knapsack Problem, the position of items in the chromosome is typically arbitrary, and preserving contiguous sections may not correspond to better solutions.

Uniform Crossover offers better exploration by independently mixing genes, which aligns well with the nature of the knapsack problem where each item’s inclusion is an independent decision. It reduces positional bias and increases the likelihood of discovering optimal combinations of items.

Crossover

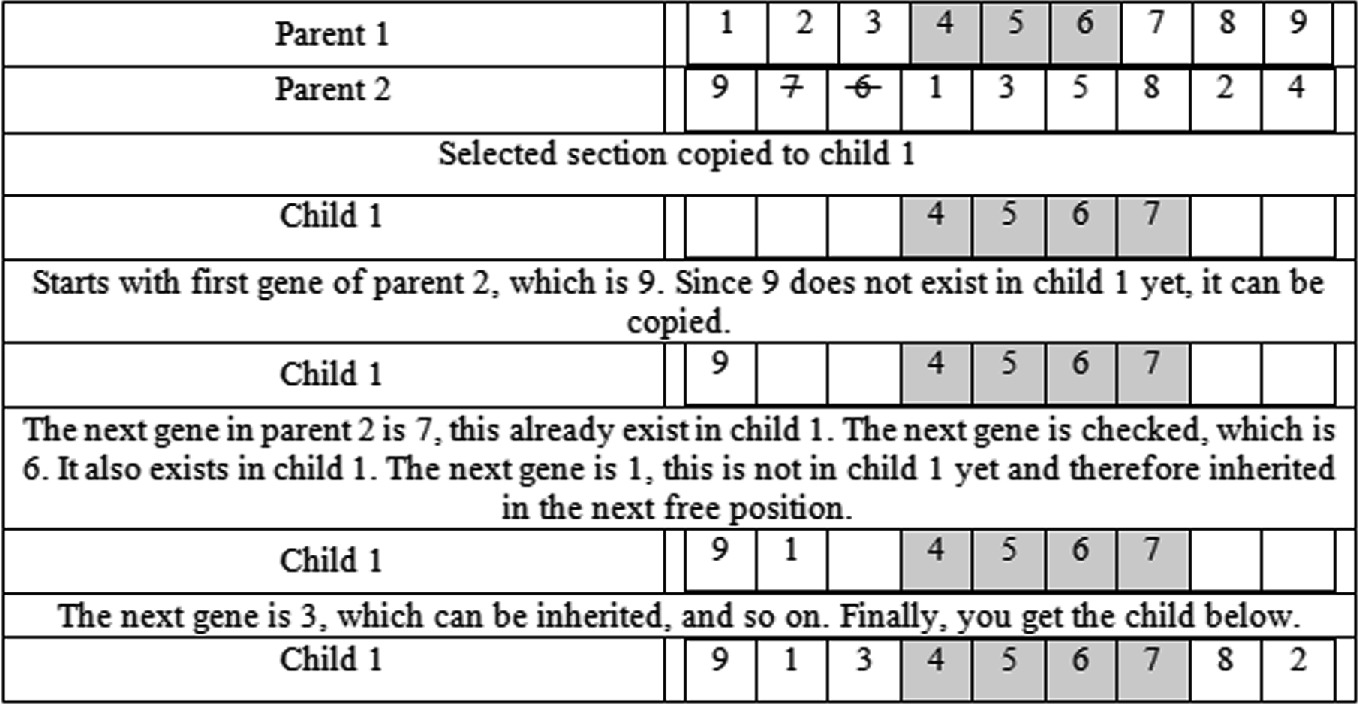
Order preserving. For each offspring, retain the sequence of elements from one parent while filling in the remaining positions with elements from the other parent, preserving their order as they appear in the second parent.

Order 1 crossover (OX)

Partially Mapped Crossover (PMX)

Comparison

Feature PMX OX
Preservation of Position High Low
Preservation of Order Partial High
Exploration vs. Exploitation Exploitation-focused Exploration-focused
Implementation Complexity Higher Lower
Application Suitability Problems with positional dependencies Problems with order dependencies

Mutation

  • Bit Flip Mutation: This involves flipping the value of a bit at a selected position within the chromosome.

    • Mutation Rate: A typical mutation rate is \(1/n\), where \(n\) represents the length of the chromosome.

Mutation

  • Replacement or Random Resetting: For integer and real-valued chromosomes, employ a random selection from the uniform distribution \(U(a, b)\) to choose a new value within the interval \([a, b]\). Similar to the bit flip operator, determine for each position whether a mutation should occur, then apply the replacement if necessary.

Mutation

  • Swap Mutation: This operator randomly selects two genes within a permutation and exchanges their positions. Such mutations facilitate the exploration of various permutations, potentially yielding improved solutions.

Remarks

When designing operators, it is critical to ensure they can explore the entire state space exhaustively.

Mutation operators should remain unbiased to maintain the integrity of the exploration process.

Comprehensive Example (1)

A Jupyter Notebook containing all lecture code has been created.

It includes tests on 25 problem instances.

In this context, the genetic algorithm consistently outperformed the greedy algorithms, matching the best greedy results in 8 cases and surpassing them in 17 cases, with improvements up to 6%.

Comprehensive Example (2)

Fredj Kharroubi conducted an empirical study on the knapsack problem, comparing the performance of several algorithms: generate-and-test, greedy search, simulated annealing, and a genetic algorithm.

Jupyter Notebook

Discussions on Hyperparameters

Population Size

  • A larger size improves genetic diversity but increases computational cost.

  • A smaller size speeds up execution but risks premature convergence.

Discussions on Hyperparameters

Mutation and Crossover Rates

  • High rates promote exploration but risk disrupting viable solutions.

  • Low rates favor exploitation but risk getting stuck in local optima.

Discussions on Hyperparameters

Selection and Tournament Size

  • Tournament selection is robust against uneven fitness distributions.

  • A medium tournament size (3-5) balances exploration and exploitation well.

Parameters

Genetic algorithms, like many machine learning and search algorithms, require hyperparameter tuning to optimize their performance.

Key hyperparameters in genetic algorithms include population size, mutation rate, crossover rate, selection method, and the number of generations.

Discussion

Like other metaheuristic approaches, genetic algorithms can become trapped in local optima. A common solution, akin to the random restart technique used in hill climbing, is to periodically reinitialize the algorithm to explore different regions of the solution space.

Doubling the population size with each restart enhances the likelihood of exploring diverse regions of the state space.

Skepticism toward GA

(Skiena 2008, 267)

[I]t is quite unnatural to model applications in terms of genetic operators like mutation and crossover on bit strings. The pseudobiology adds another level of complexity between you and your problem. Second, genetic algorithms take a very long time on nontrivial problems. [\(\ldots\)] [T]he analogy with evolution – where significant progress require [sic] millions of years – can be quite appropriate. […]

I have never encountered any problem where genetic algorithms seemed to me the right way to attack it. Further, I have never seen any computational results reported using genetic algorithms that have favorably impressed me. Stick to simulated annealing for your heuristic search voodoo needs.

Greedy: value-to-weight ratio

def greedy_knapsack_ratio(weights, values, capacity):

    num_items = len(weights)

    # Calculate value-to-weight ratio for each item
    ratio = values / (weights + 1e-6)

    # Create a list of items with their ratios and original indices
    items = list(zip(ratio, values, weights, range(num_items)))

    # Sort items by ratio in decreasing order
    items.sort(reverse=True)
    
    total_weight = 0
    total_value = 0
    solution = np.zeros(num_items, dtype=int)
    
    # Select items based on the sorted order
    for r, v, w, idx in items:
        if total_weight + w <= capacity:
            solution[idx] = 1
            total_weight += w
            total_value += v
     
    return solution, total_value, total_weight

greedy_knapsack_ratio

solution, total_value, total_weight = greedy_knapsack_ratio(weights, values, capacity)

print(f"Solution: {solution}")
print(f"Value: {total_value}")
print(f"Weight: {total_weight}")
Solution: [1 1 0 1 1 0 1 0 0 0 1 1 1 0 1 1 1 1 1 1 0 1 1 0 1 0 0 1 1 1 1 1 1 0 1 0 0
 0 1 1 0 1 1 0 1 0 0 1 1 1]
Value: 7534
Weight: 850

Frameworks

  • DEAP,
    • DEAP is an evolutionary computation framework designed for rapid prototyping and testing of ideas. It aims to make algorithms explicit and data structures transparent. The framework seamlessly integrates with parallelization mechanisms, including multiprocessing and SCOOP.
    • It has been developed at Université Laval since 2012.
  • PyGAD, 5 PyGAD applications

Genetic Programming

Definition

Genetic programming is an evolutionary algorithm-based methodology that evolves computer programs to solve problems by mimicking natural selection processes.

It automatically discovers optimal or near-optimal solutions by iteratively modifying a population of candidate programs, guided by a fitness function.

Genetic Programming

Genetic Programming

Prologue

Conclusion

  • Rather than exploring a single solution at a time, GA explore several solutions in parallel.

Comparison of SA and GA

Aspect Simulated Annealing (SA) Genetic Algorithms (GA)
Solution Representation Single solution iteratively improved Population of solutions evolved over generations
Exploration Mechanism Random moves to neighboring solutions; acceptance based on temperature Crossover and mutation generate new solutions from existing ones
Exploitation Mechanism Gradual reduction in temperature focuses search around current best solution Selection and elitism favor fitter individuals in the population
Control Parameters Temperature, cooling schedule Population size, crossover rate, mutation rate, selection method
Search Strategy Explores by accepting worse solutions at higher temperatures Explores by combining and mutating existing solutions
Balance of Exploration and Exploitation Controlled by temperature schedule Controlled by genetic operator rates and selection pressure
Escape from Local Optima Possible due to probabilistic acceptance of worse solutions Possible due to diversity in population and genetic variations
Convergence Depends on cooling schedule; may be slow for large problems Can converge prematurely without sufficient diversity

Summary

  • Metaheuristics Overview

  • Genetic Algorithms (GAs)

  • Applications of GAs

  • Components of GAs:

    • Encoding: Representation of candidate solutions (e.g., binary strings for the knapsack problem).
    • Population: A set of candidate solutions initialized randomly or by some heuristic.
    • Selection: Methods like roulette wheel and tournament selection choose fitter individuals for reproduction.
    • Crossover: Combines parts of two parents to create offspring (e.g., single-point crossover).
    • Mutation: Randomly alters genes in a chromosome to maintain genetic diversity.
    • Fitness Function: Evaluates how close a candidate solution is to the optimum.

  • Knapsack Problem Example:

    • Demonstrated how to apply GAs to the 0/1 knapsack problem.
    • Provided Python code snippets implementing GA components for the problem.
    • Showed how to generate an initial population, perform crossover and mutation, and select the next generation.
    • Compared GA solutions with optimal solutions obtained using Google’s OR-Tools.

Further Readings

Resources

Next lecture

  • We will look at the Monte Carlo Tree Search (MCTS) algorithm

References

Bye, Robin T., Magnus Gribbestad, Ramesh Chandra, and Ottar L. Osen. 2021. “A Comparison of GA Crossover and Mutation Methods for the Traveling Salesman Problem.” In Innovations in Computational Intelligence and Computer Vision, edited by Manoj Kumar Sharma, Vijaypal Singh Dhaka, Thinagaran Perumal, Nilanjan Dey, and João Manuel R. S. Tavares, 529–42. Singapore: Springer Singapore.
Cattolico, Mike, and Vincent A Cicirello. 2006. “Non-wrapping order crossover: an order preserving crossover operator that respects absolute position.” Proceedings of the 8th Annual Conference on Genetic and Evolutionary Computation, 1125–32. https://doi.org/10.1145/1143997.1144177.
Dennett, Daniel C. 1995. “Darwin’s Dangerous Idea.” The Sciences 35 (3): 34–40.
Eddaly, M., B. Jarboui, and P. Siarry. 2023. Metaheuristics for Machine Learning: New Advances and Tools. Computational Intelligence Methods and Applications. Springer Nature Singapore. https://books.google.ca/books?id=yXMtzwEACAAJ.
Gil-Rios, Miguel-Angel, Ivan Cruz-Aceves, Fernando Cervantes-Sanchez, Igor Guryev, and Juan-Manuel López-Hernández. 2021. “Automatic Enhancement of Coronary Arteries Using Convolutional Gray-Level Templates and Path-Based Metaheuristics.” In Recent Trends in Computational Intelligence Enabled Research, edited by Siddhartha Bhattacharyya, Paramartha Dutta, Debabrata Samanta, Anirban Mukherjee, and Indrajit Pan, 129–53. Academic Press.
Gregory, T. Ryan. 2009. “Understanding Natural Selection: Essential Concepts and Common Misconceptions.” Evolution: Education and Outreach 2 (2): 156–75. https://doi.org/10.1007/s12052-009-0128-1.
Holland, John H. 1973. “Genetic Algorithms and the Optimal Allocation of Trials.” SIAM Journal on Computing 2 (2): 88–105. https://doi.org/10.1137/0202009.
———. 1992. “Genetic Algorithms.” Scientific American 267: 66–73. https://www.jstor.org/stable/10.2307/24939139.
Kramer, Oliver. 2017. Genetic Algorithm Essentials. Studies in Computational Intelligence ; 679. Cham, Switzerland: Springer.
Mayr, Ernst. 1982. The Growth of Biological Thought: Diversity, Evolution, and Inheritance. Harvard University Press.
Mitchell, Melanie. 1998. An Introduction to Genetic Algorithms. Cambridge, MA, USA: MIT Press.
Oliva, D., E. H. Houssein, and S. Hinojosa. 2021. Metaheuristics in Machine Learning: Theory and Applications. Studies in Computational Intelligence. Springer International Publishing. https://books.google.ca/books?id=Zlw4EAAAQBAJ.
Russell, Stuart, and Peter Norvig. 2020. Artificial Intelligence: A Modern Approach. 4th ed. Pearson. http://aima.cs.berkeley.edu/.
Santos Amorim, Elisa Portes dos, Carolina Ribeiro Xavier, Ricardo Silva Campos, and Rodrigo Weber dos Santos. 2012. “Comparison Between Genetic Algorithms and Differential Evolution for Solving the History Matching Problem.” In Computational Science and Its Applications - ICCSA 2012 - 12th International Conference, Salvador de Bahia, Brazil, June 18-21, 2012, Proceedings, Part I, edited by Beniamino Murgante, Osvaldo Gervasi, Sanjay Misra, Nadia Nedjah, Ana Maria A. C. Rocha, David Taniar, and Bernady O. Apduhan, 7333:635–48. Lecture Notes in Computer Science. Springer. https://doi.org/10.1007/978-3-642-31125-3\_48.
Skiena, Steven S. 2008. The Algorithm Design Manual. London: Springer. https://doi.org/10.1007/978-1-84800-070-4.

Marcel Turcotte

[email protected]

School of Electrical Engineering and Computer Science (EECS)

University of Ottawa

turcotte.xyz/teaching/csi-4106