Évaluation des modèles et d’ajustement des hyperparamètres

CSI 4506 - Automne 2024

Marcel Turcotte

Version: oct. 5, 2024 13h02

Préambule

Citation du jour

Super Intelligence tiré de The Future with Hannah Fry, diffusé le 12 septembre 2024.

Objectifs d’apprentissage

1. Comprendre l’objectif de la division des données :
   • Décrire les rôles des ensembles d’entraînement, de validation et de test dans l’évaluation des modèles.
   • Expliquer pourquoi et comment les ensembles de données sont divisés pour un apprentissage et une évaluation efficaces des modèles.
2. Expliquer les techniques de validation croisée :
   • Définir la validation croisée et son importance dans l’évaluation des modèles.
   • Illustrer le processus de validation croisée \(k\)-fold et ses avantages par rapport à une seule division entraînement-test.
   • Discuter des concepts de sur-apprentissage et de sous-apprentissage dans le contexte de la validation croisée.
3. Ajustement des hyperparamètres :
   • Expliquer la différence entre les paramètres de modèle et les hyperparamètres.
   • Décrire les méthodes de réglage des hyperparamètres, y compris la recherche en grille et la recherche aléatoire.
   • Implémenter l’ajustement des hyperparamètres à l’aide de GridSearchCV dans scikit-learn.
4. Évaluer la performance du modèle :
   • Interpréter les résultats de la validation croisée et comprendre des métriques telles que la moyenne et l’écart-type des scores.
   • Discuter de la manière dont la validation croisée aide à évaluer la généralisation du modèle et à réduire la variabilité.
5. Flux de travail de l’ingénierie en apprentissage automatique :
   • Décrire les étapes impliquées dans la préparation des données pour les modèles d’apprentissage automatique.
   • Utiliser les pipelines scikit-learn pour un prétraitement efficace des données et un entraînement des modèles.
   • Insister sur l’importance des transformations de données cohérentes entre les environnements d’entraînement et de production.
6. Évaluation critique des modèles d’apprentissage automatique :
   • Évaluer les limites et les défis liés à l’ajustement des hyperparamètres et à la sélection de modèles.
   • Reconnaître les pièges potentiels dans le prétraitement des données, tels qu’une gestion incorrecte des valeurs manquantes ou un encodage incohérent.
   • Plaider en faveur de tests et validations approfondis pour garantir la fiabilité et la généralisabilité du modèle.
7. Intégration des connaissances dans des applications pratiques :
   • Appliquer les concepts appris à des ensembles de données réels (par exemple, ensembles de données OpenML tels que ‘diabetes’ et ‘adult’).
   • Interpréter et analyser les résultats des évaluations de modèles et des expériences.
   • Développer une compréhension complète du pipeline d’apprentissage automatique de bout en bout.

Les objectifs d’apprentissage ci-haut ont été générés par le modèle d’OpenAI, o1, à partir du contenu du cours.

Introduction

Ensemble de données - openml

www.openml.org

OpenML est une plateforme ouverte pour partager des ensembles de données, des algorithmes et des expériences - pour apprendre à mieux apprendre, ensemble.

import numpy as np
np.random.seed(42)

from sklearn.datasets import fetch_openml

diabetes = fetch_openml(name='diabetes', version=1)
print(diabetes.DESCR)

L’ensemble de données utilisé aujourd’hui est le PIMA, qui contient 768 exemples et 8 attributs numériques. La nature numérique de ces attributs facilite notre analyse. De plus, puisque les données proviennent d’un article publié, elles reflètent probablement une collecte de données soignée, ce qui pourrait conduire à des résultats robustes, étant donné que les auteurs auraient eu besoin de données de haute qualité pour étayer leur publication.

Ensemble de données - openml

Author: Vincent Sigillito

Source: Obtained from UCI

Please cite: UCI citation policy

1. Title: Pima Indians Diabetes Database

2. Sources:

   1. Original owners: National Institute of Diabetes and Digestive and Kidney Diseases
   2. Donor of database: Vincent Sigillito ([email protected]) Research Center, RMI Group Leader Applied Physics Laboratory The Johns Hopkins University Johns Hopkins Road Laurel, MD 20707 (301) 953-6231
   3. Date received: 9 May 1990

3. Past Usage:

   1. Smith,_J.W., Everhart,_J.E., Dickson,_W.C., Knowler,_W.C., & Johannes,_R.S. (1988). Using the ADAP learning algorithm to forecast the onset of diabetes mellitus. In {it Proceedings of the Symposium on Computer Applications and Medical Care} (pp. 261–265). IEEE Computer Society Press.

      The diagnostic, binary-valued variable investigated is whether the patient shows signs of diabetes according to World Health Organization criteria (i.e., if the 2 hour post-load plasma glucose was at least 200 mg/dl at any survey examination or if found during routine medical care). The population lives near Phoenix, Arizona, USA.

      Results: Their ADAP algorithm makes a real-valued prediction between 0 and 1. This was transformed into a binary decision using a cutoff of 0.448. Using 576 training instances, the sensitivity and specificity of their algorithm was 76% on the remaining 192 instances.

4. Relevant Information: Several constraints were placed on the selection of these instances from a larger database. In particular, all patients here are females at least 21 years old of Pima Indian heritage. ADAP is an adaptive learning routine that generates and executes digital analogs of perceptron-like devices. It is a unique algorithm; see the paper for details.

5. Number of Instances: 768

6. Number of Attributes: 8 plus class

7. For Each Attribute: (all numeric-valued)

   1. Number of times pregnant
   2. Plasma glucose concentration a 2 hours in an oral glucose tolerance test
   3. Diastolic blood pressure (mm Hg)
   4. Triceps skin fold thickness (mm)
   5. 2-Hour serum insulin (mu U/ml)
   6. Body mass index (weight in kg/(height in m)^2)
   7. Diabetes pedigree function
   8. Age (years)
   9. Class variable (0 or 1)

8. Missing Attribute Values: None

9. Class Distribution: (class value 1 is interpreted as “tested positive for diabetes”)

   Class Value Number of instances 0 500 1 268

10. Brief statistical analysis:

    Attribute number: Mean: Standard Deviation:

    1.                 3.8     3.4

    2.               120.9    32.0

    3.                69.1    19.4

    4.                20.5    16.0

    5.                79.8   115.2

    6.                32.0     7.9

    7.                 0.5     0.3

    8.                33.2    11.8

Relabeled values in attribute ‘class’ From: 0 To: tested_negative
From: 1 To: tested_positive

Downloaded from openml.org.

Ensemble de données - return_X_y

fetch_openml renvoie un Bunch, un DataFrame ou X et y

X, y = fetch_openml(name='diabetes', version=1, return_X_y=True)

Déséquilibre modéré (rapport inférieur à 3 ou 4)

print(y.value_counts())

class
tested_negative    500
tested_positive    268
Name: count, dtype: int64

Conversion des étiquettes cibles en 0 et 1

y = y.map({'tested_negative': 0, 'tested_positive': 1})

Évaluation croisée

Ensemble d’entraînement et ensemble de test

Parfois appelée holdout method.

• Recommandation: Allouer 80% de votre ensemble de données pour l’entraînement et réserver les 20% restants pour les tests.

• Ensemble d’entraînement: Sous-ensemble de données utilisé pour entraîner votre modèle.

• Ensemble de test: Sous-ensemble indépendant utilisé exclusivement lors de l’étape finale pour évaluer les performances du modèle.

Ratios courants d’entraînement et de test

1. Division 80:20:
   • Ensemble d’entraînement: 80% des données
   • Ensemble de test: 20% des données
   • Ce partage est un choix par défaut largement utilisé qui permet un équilibre entre avoir suffisamment de données pour entraîner le modèle et suffisamment de données pour évaluer ses performances.
2. Division 90:10:
   • Ensemble d’entraînement: 90% des données
   • Ensemble de test: 10% des données
   • Ce partage peut être utilisé lorsque l’ensemble de données est très grand, garantissant une quantité substantielle de données pour l’entraînement tout en conservant un ensemble de test de taille décente.

Considérations pour choisir le ratio

1. Taille de l’ensemble de données:
   • Pour les grands ensembles de données, une plus petite proportion peut être réservée aux tests (par exemple, 90:10), car même 10% d’un grand ensemble de données peut fournir une évaluation robuste.
2. Complexité du modèle:
   • Les modèles complexes avec de nombreux paramètres peuvent nécessiter davantage de données d’entraînement pour éviter le sur-apprentissage, suggérant un ensemble d’entraînement plus grand.
3. Ensemble de validation:
   • Voir la discussion ci-dessous.
4. Ensembles de données déséquilibrés:
   • Pour les ensembles de données déséquilibrés, il est essentiel de veiller à ce que les ensembles d’entraînement et de test représentent adéquatement la répartition des classes. L’échantillonnage stratifié peut être utilisé pour maintenir les proportions de classes dans les deux ensembles.

Ensemble d’entraînement et ensemble de test

Erreur d’entraînement :

• En général, elle a tendance à être faible
• Obtenue en optimisant les algorithmes d’apprentissage pour minimiser l’erreur à travers l’ajustement des paramètres (par exemple, les poids)

Ensemble d’entraînement et ensemble de test

Erreur de généralisation : L’erreur observée lorsque le modèle est évalué sur des données nouvelles, non vues.

Ensemble d’entraînement et ensemble de test

Sous-apprentissage :

• Erreur d’entraînement élevée
• Le modèle est trop simple pour capturer les motifs sous-jacents
• Mauvaise performance à la fois sur les données d’entraînement et les nouvelles données

Sur-apprentissage :

• Faible erreur d’entraînement, mais erreur de généralisation élevée
• Le modèle capture le bruit ou des motifs non pertinents
• Mauvaise performance sur les nouvelles données non vues

Définition

La validation croisée (cross-validation) est une méthode utilisée pour évaluer et améliorer les performances des modèles d’apprentissage automatique.

Elle consiste à partitionner l’ensemble de données en plusieurs sous-ensembles, en entraînant le modèle sur certains sous-ensembles tout en le validant sur les autres.

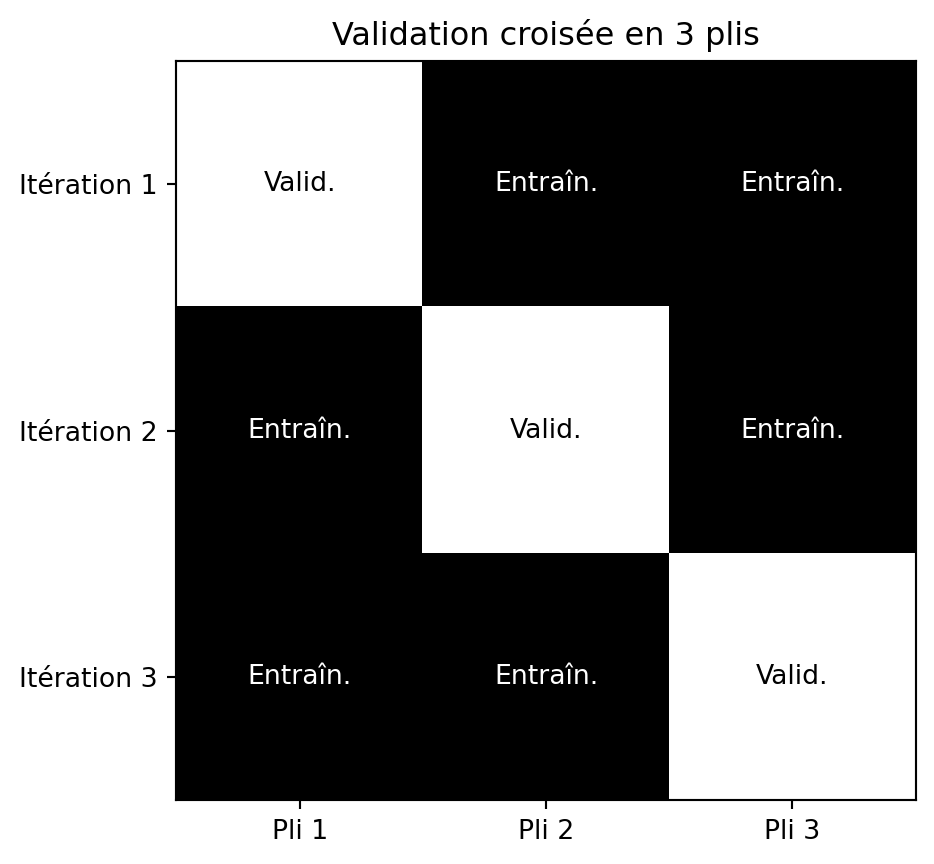
Validation croisée en \(k\) parties (k-fold)

1. Diviser l’ensemble de données en \(k\) parties de taille égale (plis).
2. Entraînement et validation :
   • À chaque itération, un pli est utilisé comme ensemble de validation, les \(k\)-1 plis restants sont utilisés comme ensemble d’entraînement.
3. Évaluation: Les performances du modèle sont évaluées à chaque itération, ce qui donne \(k\) mesures de performance.
4. Agrégation: Les statistiques sont calculées à partir des \(k\) mesures de performance.

Les choix courants pour la valeur de \(k\) sont 3, 5, 7 et 10.

Validation croisée en 3 plis

À chaque itération, \(2/3\) de l’ensemble de données est utilisé pour l’entraînement et \(1/3\) pour la validation.

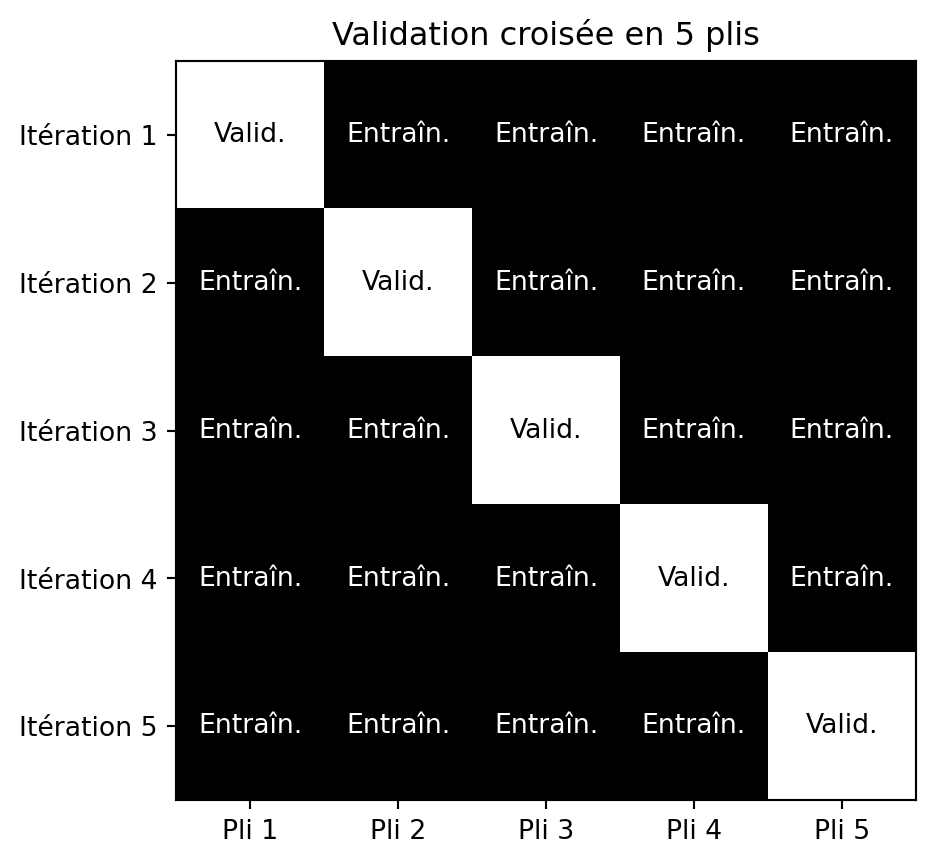
Validation croisée en 5 plis

À chaque itération, \(4/5\) de l’ensemble de données est utilisé pour l’entraînement et \(1/5\) pour la validation.

Évaluation de modèle plus fiable

• Estimation plus fiable des performances du modèle par rapport à une seule division entraînement-test.
• Réduit la variabilité associée à une seule division, conduisant à une évaluation plus stable et moins biaisée.
• Pour de grandes valeurs de \(k\), considérez la moyenne, variance, et intervalle de confiance.

Meilleure généralisation

• Aide à évaluer comment le modèle généralise à un ensemble de données indépendant.
• Garantit que les performances du modèle ne sont ni trop optimistes ni trop pessimistes en moyennant les résultats sur plusieurs plis.

Utilisation efficace des données

• Particulièrement bénéfique pour les petits ensembles de données, la validation croisée garantit que chaque point de données est utilisé à la fois pour l’entraînement et la validation.
• Cela maximise l’utilisation des données disponibles, conduisant à un entraînement de modèle plus précis et fiable.

Certaines exemples sont plus informatifs pour les algorithmes d’apprentissage, notamment ceux situés près de la frontière de décision.

Ajustement des hyperparamètres

• Couramment utilisé pendant l’ajustement des hyperparamètres, permettant de sélectionner les meilleurs paramètres du modèle en fonction de leurs performances sur plusieurs plis.
• Cela aide à identifier la configuration optimale qui équilibre biais et variance.

Défis

• Coût computationnel: Nécessite plusieurs entraînements de modèles.
  • Leave-One-Out (LOO): Cas extrême où \(k = N\).
• Déséquilibre des classes: Les plis peuvent ne pas représenter correctement les classes minoritaires.
  • Utilisez la validation croisée stratifiée pour maintenir les proportions de classes.
• Complexité: Implémentation sujette à des erreurs, en particulier pour la validation croisée imbriquée, les bootstrap ou l’intégration dans des pipelines plus complexes.

La validation croisée leave-one-out (LOO-CV) peut conduire à une évaluation de performance trop optimiste, particulièrement dans certains contextes.

Voici pourquoi :

1. Haute variance : Dans la LOO-CV, chaque itération utilise presque toutes les données pour l’entraînement, ne laissant qu’une seule instance pour le test. Cela peut entraîner une haute variance de l’erreur de test à travers les itérations, car le modèle est entraîné sur presque l’ensemble du jeu de données. Étant donné que chaque ensemble d’entraînement est très similaire au jeu de données complet, cela peut conduire à des estimations trop optimistes de l’erreur de généralisation, surtout lorsque le jeu de données est petit ou que le modèle a une variance élevée (par exemple, les arbres de décision ou les k-plus proches voisins).

2. Surapprentissage : Comme la LOO-CV utilise presque l’intégralité du jeu de données pour l’entraînement à chaque itération, les modèles complexes (surtout ceux sujets au surapprentissage) peuvent s’ajuster très étroitement aux données, ce qui peut résulter en une erreur d’entraînement faible mais en une erreur de test trompeusement faible dans certains cas.

3. Évaluation limitée de la généralisation : La LOO-CV peut ne pas fournir une estimation fiable de la capacité de généralisation du modèle à des données complètement nouvelles, car la différence entre l’ensemble d’entraînement et le jeu de données complet est minimale, ce qui réduit l’écart entre les performances d’entraînement et de test.

En pratique, cela peut rendre l’évaluation plus optimiste qu’elle ne le serait avec des méthodes plus robustes comme la validation croisée k-fold, où les ensembles de test sont plus grands et où le modèle a moins d’opportunités de surapprendre les données d’entraînement.

cross_val_score

from sklearn import tree

clf = tree.DecisionTreeClassifier()

from sklearn.model_selection import cross_val_score    

clf_scores = cross_val_score(clf, X, y, cv=5)

print("\nScores:", clf_scores)
print(f"\nMoyenne: {clf_scores.mean():.2f}")
print(f"\nÉcart-type: {clf_scores.std():.2f}")

Scores: [0.71428571 0.66883117 0.71428571 0.79738562 0.73202614]

Moyenne: 0.73

Écart-type: 0.04

Comme discuté précédemment, une limitation significative des arbres de décision est leur tendance à sur-apprendre, ce qui conduit à une forte variance lorsqu’ils sont appliqués à de nouveaux ensembles de données. Ce problème est visible dans la variabilité des performances observée, avec une précision allant de 67% à 79%, ce qui est indésirable pour obtenir une généralisation robuste du modèle.

sklearn.model_selection.cross_val_score, voir aussi cross_validate.

Ajustement des hyperparamètres

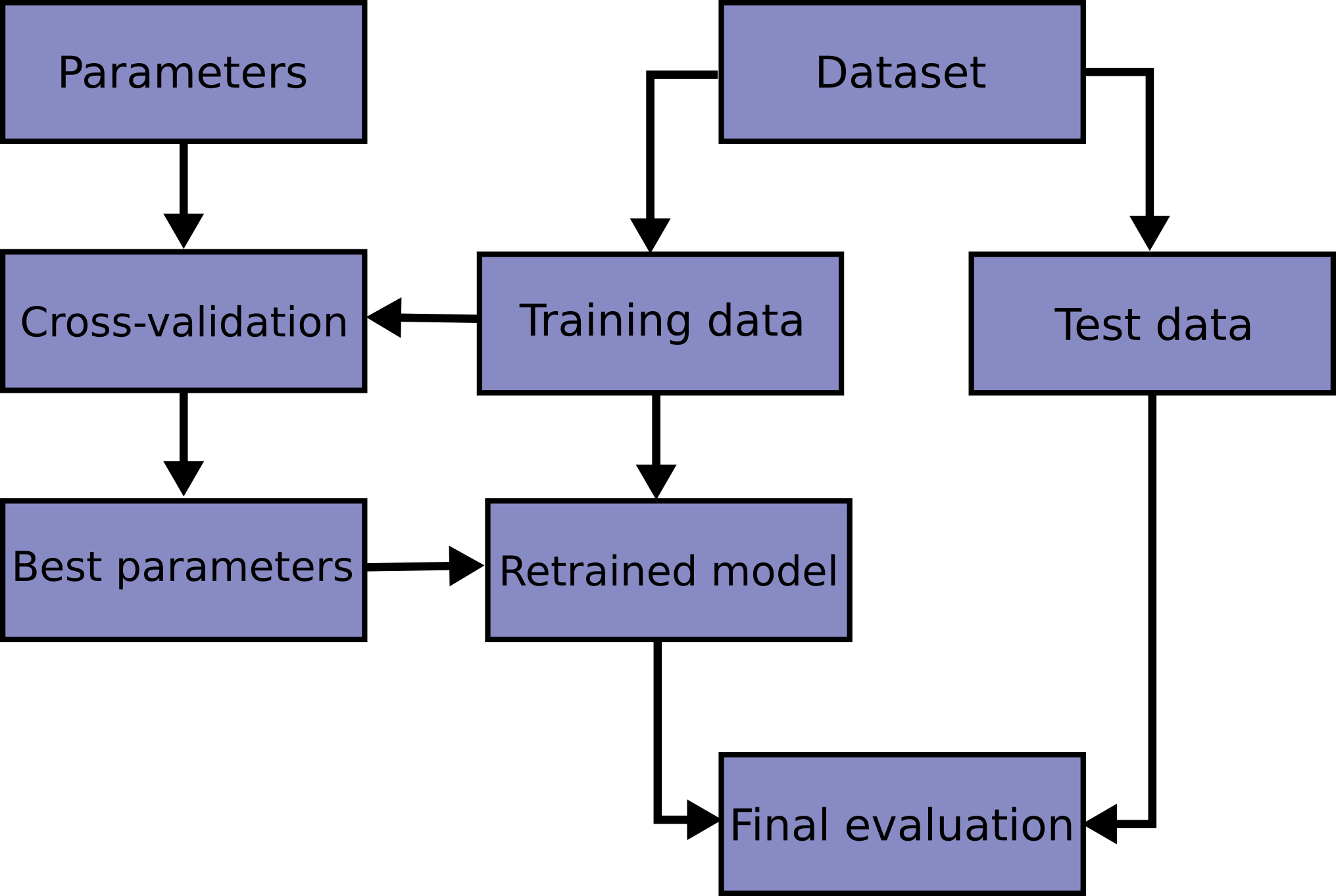
Flux de travail (Workflow)

L’image ci-dessus introduit implicitement trois catégories de sous-ensembles de données : entraînement, validation, et test.

Attribution: Cross-validation: evaluating estimator performance

Implémentation du flux de travail

from sklearn.datasets import fetch_openml

X, y = fetch_openml(name='diabetes', version=1, return_X_y=True)

y = y.map({'tested_negative': 0, 'tested_positive': 1})

from sklearn.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.1)

Afin de simplifier ces notes de cours, nous n’avons appliqué aucune étape de prétraitement.

Définition

Un hyperparamètre est une configuration externe au modèle qui est définie avant le processus d’apprentissage et qui régit le processus d’apprentissage, influençant les performances et la complexité du modèle.

Les poids d’un modèle, qui sont appris par l’algorithme d’apprentissage, sont souvent appelés paramètres du modèle. Pour éviter toute confusion, les paramètres définis par l’utilisateur, tels que le taux d’apprentissage \(\alpha\), sont appelés hyperparamètres. Contrairement aux paramètres de modèle, les hyperparamètres ne sont pas appris par l’algorithme d’apprentissage.

Hyperparamètres - Arbre de décision

• criterion: gini, entropy, log_loss, mesure la qualité d’une scission.
• max_depth: limite le nombre de niveaux dans l’arbre pour éviter le sur-apprentissage.

Voir: DecisionTreeClassifier

Hyperparamètres - Régression logistique

• penalty: l1 ou l2, aide à éviter le sur-apprentissage.
• solver: liblinear, newton-cg, lbfgs, sag, saga.
• max_iter: nombre maximal d’itérations pour que les solveurs convergent.
• tol: critère d’arrêt, les petites valeurs signifient une plus grande précision.

Voir: LogisticRegression et SGDClassifier.

Hyperparamètres - KNN

• n_neighbors: nombre de voisins à utiliser pour les requêtes de \(k\)-voisins.
• weights: uniform ou distance, poids égal ou basé sur la distance.

Voir: KNeighborsClassifier

Expérience : max_depth

for value in [3, 5, 7, None]:

  clf = tree.DecisionTreeClassifier(max_depth=value)

  clf_scores = cross_val_score(clf, X_train, y_train, cv=10)

  print("\nmax_depth = ", value)
  print(f"Moyenne: {clf_scores.mean():.2f}")
  print(f"Écart-type: {clf_scores.std():.2f}")

max_depth =  3
Moyenne: 0.74
Écart-type: 0.04

max_depth =  5
Moyenne: 0.76
Écart-type: 0.04

max_depth =  7
Moyenne: 0.73
Écart-type: 0.04

max_depth =  None
Moyenne: 0.71
Écart-type: 0.05

Expérience : criterion

for value in ["gini", "entropy", "log_loss"]:

  clf = tree.DecisionTreeClassifier(max_depth=5, criterion=value)

  clf_scores = cross_val_score(clf, X_train, y_train, cv=10)

  print("\ncriterion = ", value)
  print(f"Moyenne: {clf_scores.mean():.2f}")
  print(f"Écart-type: {clf_scores.std():.2f}")

criterion =  gini
Moyenne: 0.76
Écart-type: 0.04

criterion =  entropy
Moyenne: 0.75
Écart-type: 0.05

criterion =  log_loss
Moyenne: 0.75
Écart-type: 0.05

Pour ce problème et cet ensemble de données spécifiques, le paramètre criterion a un impact limité sur le processus d’apprentissage.

Expérience : n_neighbors

from sklearn.neighbors import KNeighborsClassifier

for value in range(1, 11):

  clf = KNeighborsClassifier(n_neighbors=value)

  clf_scores = cross_val_score(clf, X_train, y_train, cv=10)

  print("\nn_neighbors = ", value)
  print(f"Moyenne: {clf_scores.mean():.2f}")
  print(f"Écart-type: {clf_scores.std():.2f}")

Expérience : n_neighbors

n_neighbors =  1
Moyenne: 0.67
Écart-type: 0.05

n_neighbors =  2
Moyenne: 0.71
Écart-type: 0.03

n_neighbors =  3
Moyenne: 0.69
Écart-type: 0.05

n_neighbors =  4
Moyenne: 0.73
Écart-type: 0.03

n_neighbors =  5
Moyenne: 0.72
Écart-type: 0.03

n_neighbors =  6
Moyenne: 0.73
Écart-type: 0.05

n_neighbors =  7
Moyenne: 0.74
Écart-type: 0.04

n_neighbors =  8
Moyenne: 0.75
Écart-type: 0.04

n_neighbors =  9
Moyenne: 0.73
Écart-type: 0.05

n_neighbors =  10
Moyenne: 0.73
Écart-type: 0.04

Expérience : weights

from sklearn.neighbors import KNeighborsClassifier

for value in ["uniform", "distance"]:

  clf = KNeighborsClassifier(n_neighbors=5, weights=value)

  clf_scores = cross_val_score(clf, X_train, y_train, cv=10)

  print("\nweights = ", value)
  print(f"Moyenne: {clf_scores.mean():.2f}")
  print(f"Écart-type: {clf_scores.std():.2f}")

weights =  uniform
Moyenne: 0.72
Écart-type: 0.03

weights =  distance
Moyenne: 0.73
Écart-type: 0.04

Pour ce problème et cet ensemble de données spécifiques, le paramètre weights a un impact limité sur le processus d’apprentissage.

À ce stade, vous pourriez émettre l’hypothèse que certaines combinaisons d’hyperparamètres pourraient être plus optimales que d’autres.

Recherche en grille (grid search)

• De nombreux hyperparamètres nécessitent un ajustement

  • Principal désavantage des algorithmes d’apprentissage automatique

• L’exploration manuelle des combinaisons est fastidieuse

• La recherche en grille est plus systématique

  1. Énumérer toutes les combinaisons possibles d’hyperparamètres

  2. Entraîner sur l’ensemble d’entraînement, évaluer sur l’ensemble de validation

L’ensemble d’entraînement mentionné ici est différent de celui mentionné précédemment. À chaque itération du processus de validation croisée en \(k\) plis, un ensemble d’entraînement et un ensemble de validation uniques sont créés.

Dans certains contextes, le choix du modèle lui-même peut être considéré comme un hyperparamètre. Par exemple, lors de la sélection de modèles au sein d’un pipeline d’apprentissage automatique, différents algorithmes (par exemple, arbres de décision, machines à vecteurs de support, réseaux neuronaux) peuvent être traités comme des hyperparamètres. Cela permet de sélectionner le modèle offrant les meilleures performances via des processus automatisés comme la recherche en grille ou la recherche aléatoire, en parallèle du réglage d’autres hyperparamètres.

Ainsi, bien que traditionnellement les hyperparamètres fassent référence aux paramètres à l’intérieur d’un modèle spécifique, le choix du modèle peut également être intégré dans des cadres d’optimisation d’hyperparamètres.

Initialement, essayez des puissances de 2 ou de 10. Ensuite, affinez avec une recherche en grille autour des valeurs optimales si le temps le permet.

GridSearchCV

from sklearn.model_selection import GridSearchCV

param_grid = [
  {'max_depth': range(1, 10),
   'criterion': ["gini", "entropy", "log_loss"]}
]

clf = tree.DecisionTreeClassifier()

grid_search = GridSearchCV(clf, param_grid, cv=5)

grid_search.fit(X_train, y_train)

(grid_search.best_params_, grid_search.best_score_)

({'criterion': 'gini', 'max_depth': 5}, 0.7481910124074653)

GridSearchCV

param_grid = [
  {'n_neighbors': range(1, 16),
   'weights': ["uniform", "distance"]}
]

clf = KNeighborsClassifier()

grid_search = GridSearchCV(clf, param_grid, cv=5)

grid_search.fit(X_train, y_train)

(grid_search.best_params_, grid_search.best_score_)

({'n_neighbors': 14, 'weights': 'uniform'}, 0.7554165363361485)

La variable param_grid contient un dictionnaire spécifiant les noms des paramètres à ajuster, ainsi que les valeurs respectives à tester.

Dans cet exemple, les paramètres n_neighbors et weights sont ajustés. Cependant, d’autres paramètres pourraient être inclus si nécessaire.

GridSearchCV

from sklearn.linear_model import LogisticRegression

# 2 * 5 * 5 * 3 = 150 tests!

param_grid = [
  {'penalty': ["l1", "l2", None],
   'solver' : ['liblinear', 'newton-cg', 'lbfgs', 'sag', 'saga'],
   'max_iter' : [100, 200, 400, 800, 1600],
   'tol' : [0.01, 0.001, 0.0001]}
]

clf = LogisticRegression()

grid_search = GridSearchCV(clf, param_grid, cv=5)

grid_search.fit(X_train, y_train)

(grid_search.best_params_, grid_search.best_score_)

({'max_iter': 100, 'penalty': 'l2', 'solver': 'newton-cg', 'tol': 0.001},
 0.7756646856427901)

Recherche aléatoire

• Grand nombre de combinaisons (beaucoup d’hyperparamètres, beaucoup de valeurs)
• Utiliser RandomizedSearchCV :
  • Fournir une liste de valeurs ou une distribution de probabilités pour les hyperparamètres
  • Spécifier le nombre d’itérations (combinaisons à essayer)
  • Temps d’exécution prévisible

Voir : Comparing randomized search and grid search for hyperparameter estimation.

Flux de travail

Comme l’illustre cet exemple, en plus d’évaluer diverses valeurs d’hyperparamètres, plusieurs modèles peuvent également être testés.

Attribution: Cross-validation: evaluating estimator performance

Enfin, nous procédons aux tests

clf = LogisticRegression(max_iter=100, penalty='l2', solver='newton-cg', tol=0.001)

clf.fit(X_train, y_train)

y_pred = clf.predict(X_test)

from sklearn.metrics import classification_report

print(classification_report(y_test, y_pred))

              precision    recall  f1-score   support

           0       0.83      0.83      0.83        52
           1       0.64      0.64      0.64        25

    accuracy                           0.77        77
   macro avg       0.73      0.73      0.73        77
weighted avg       0.77      0.77      0.77        77

Il semble que nous soyons confrontés à un problème de déséquilibre des classes, qui aurait dû être identifié plus tôt dans notre flux de travail!

Prologue

Résumé

• Validation croisée et ajustement des hyperparamètres : Clé pour prévenir le surapprentissage et optimiser les performances.

Prochain cours

• Ingénierie de l’apprentissage automatique.

Références

Russell, Stuart, et Peter Norvig. 2020. Artificial Intelligence: A Modern Approach. 4ᵉ éd. Pearson. http://aima.cs.berkeley.edu/.

Marcel Turcotte

[email protected]

École de science informatique et de génie électrique (SIGE)

Université d’Ottawa