Recherche adversariale
CSI 4106 - Automne 2024
Version: nov. 27, 2024 07h40
Préambule
Citation du jour
Recherche adversariale
Cette présentation examine les environnements compétitifs où plusieurs agents ont des objectifs conflictuels, ce qui entraîne des problèmes de recherche adversariale.
Objectifs d’apprentissage
Expliquer les concepts de jeu à somme nulle (zero-sum game)
Formuler des stratégies pour ne jamais perdre au Tic-Tac-Toe, quel que soit le coup de l’adversaire
Utiliser l’algorithme minimax pour déterminer les coups optimaux dans des contextes adversariaux
Articuler comment l’élagage alpha-bêta réduit le nombre de nœuds évalués sans affecter les résultats
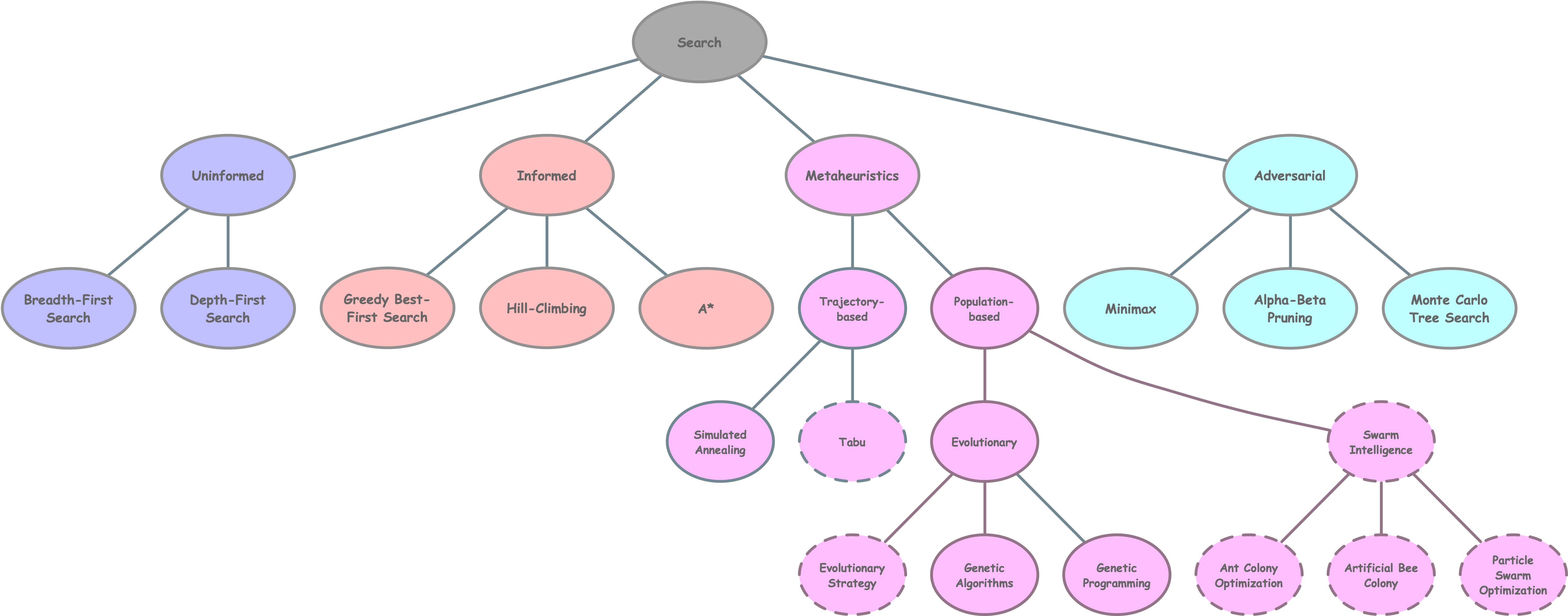
Recherche
Introduction
Types de jeux
Déterministes ou stochastiques
Un, deux, ou plusieurs joueurs
À somme nulle ou non
Information parfaite ou non
Définition
Les jeux à somme nulle (zero-sum games) sont des scénarios compétitifs où le gain d’un joueur est exactement compensé par la perte d’un autre joueur, entraînant un changement net de zéro en termes de richesse ou de bénéfice total.
Jeux déterministes
États : \(S\) (\(S_0\) à \(S_k\))
Joueurs : \(P = \{1, N\}\)
Actions : \(A\) (dépend de \(P\) et \(S\))
Fonction de transition : \(S \times A \rightarrow S\)
Un état final : \(S_\mathrm{final}\)
Récompense ou utilité : \(S_\mathrm{final}, p\)
Développer une politique \(S_0 \rightarrow S_\mathrm{final}\).
Qu’en pensez-vous ?
Envisagez de jouer au tic-tac-toe.
Pouvez-vous garantir une stratégie pour ne jamais perdre, indépendamment des coups de votre adversaire ?
Étendez cette analyse à des jeux comme les échecs ou le Go.
Tic-Tac-Toe
get_valid_moves
make_move
is_terminal
def is_terminal(state):
# Vérifie les lignes, les colonnes et les diagonales pour une victoire
lines = []
lines.extend(state) # Lignes
lines.extend(state.T) # Colonnes
lines.append(np.diagonal(state)) # Diagonale principale
lines.append(np.diagonal(np.fliplr(state))) # Anti-diagonale
for line in lines:
if np.all(line == 'X') or np.all(line == 'O'):
return True
# Vérifie s'il y a un match nul (pas d'espaces vides)
if ' ' not in state:
return True
return Falseget_opponent
count_valid_sequences
Le nombre total de séquences valides est : 255,168Symétrie (digression)
Le tic-tac-toe possède 8 transformations symétriques (4 rotations et 4 réflexions).
En les considérant, de nombreuses séquences de jeu qui diffèrent dans l’ordre brut des coups deviennent équivalentes.
Le nombre de séquences de coups uniques est de 26 830, tandis que le nombre de positions de plateau uniques est de 765.
Arbre de Recherche
La taille de l’arbre de recherche pour le jeu de tic-tac-toe est relativement petite, ce qui le rend adapté comme exemple continu dans les discussions ultérieures.
Comment cela se compare-t-il aux arbres de recherche pour les échecs et le Go ?
Arbre de Recherche
Échecs : \(35^{80} \sim 10^{123}\)
Go : \(361! \sim 10^{768}\)
Définition
Le jeu optimal consiste à exécuter le meilleur coup possible à chaque étape pour maximiser les chances de gagner ou les résultats.
Dans les jeux à information parfaite comme le tic-tac-toe ou les échecs, cela nécessite d’anticiper les coups de l’adversaire et de choisir des actions qui améliorent sa position ou minimisent les pertes.
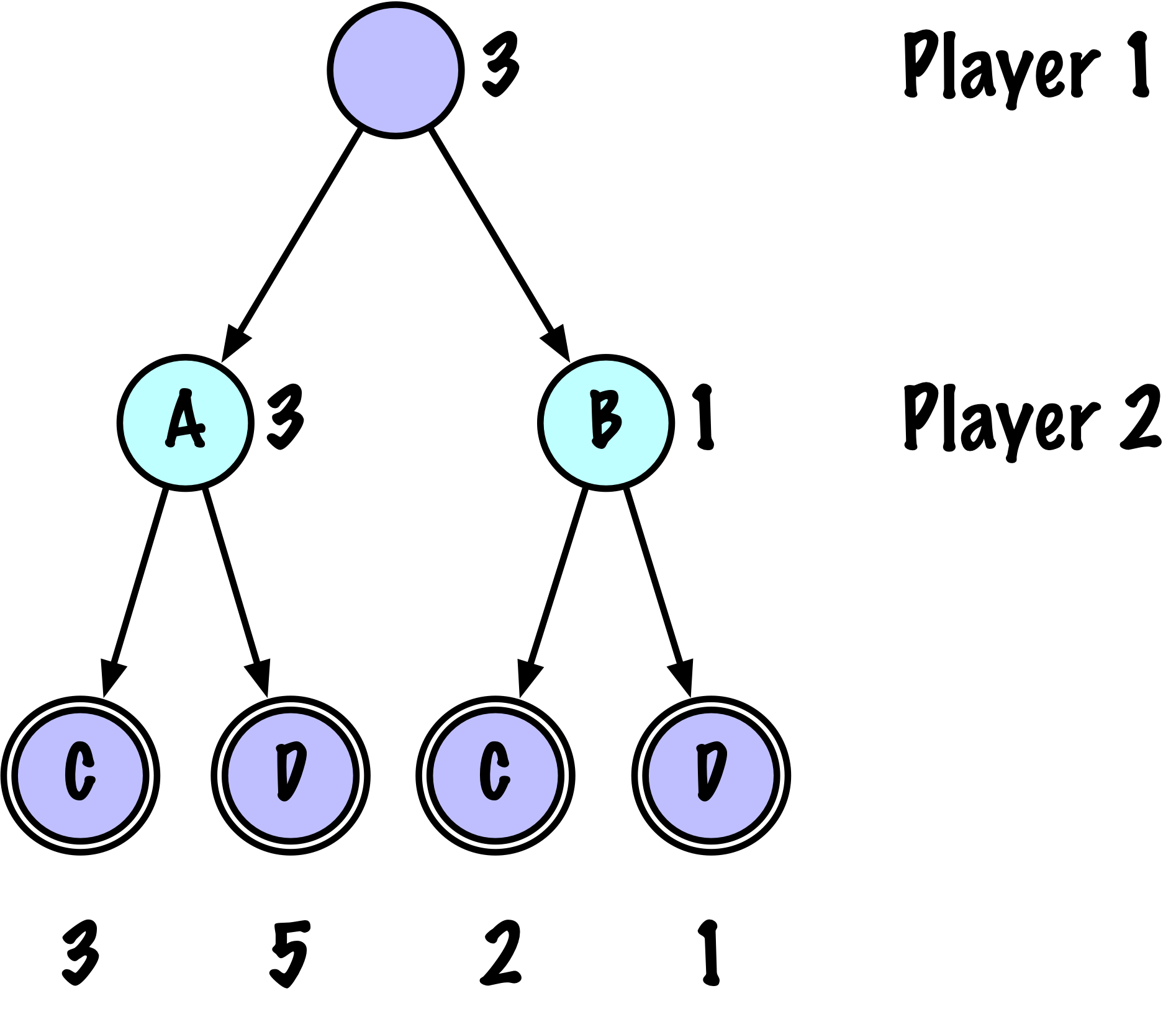
Jeu à deux coups
Configuration du jeu
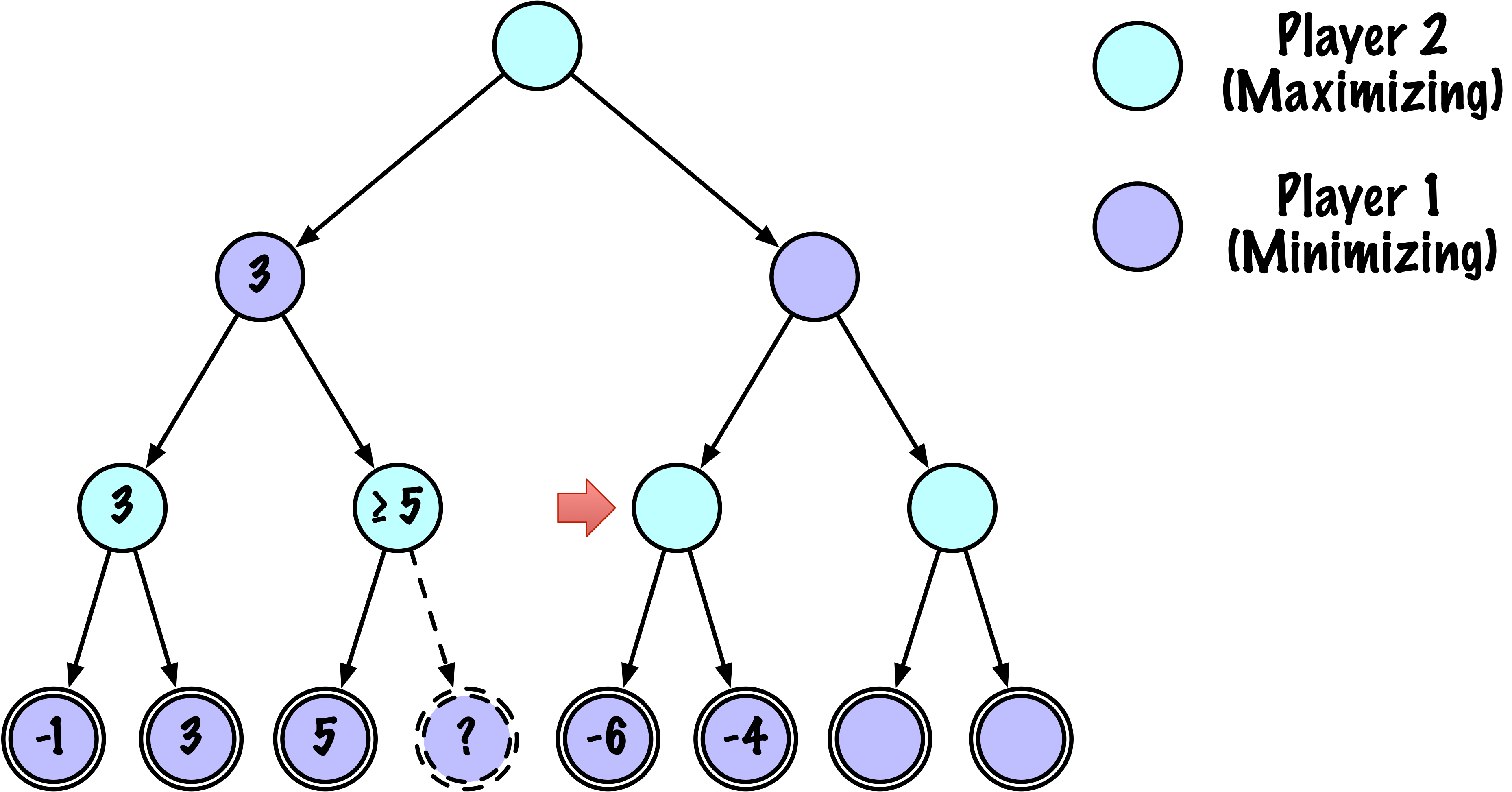
Le jeu commence par un unique point de décision pour le Joueur 1, qui a deux coups possibles : \(A\) et \(B\).
Chacun de ces coups mène à un point de décision pour le Joueur 2, qui a également deux réponses possibles : \(C\) et \(D\).
Le jeu se termine après le coup du Joueur 2, aboutissant à un état terminal avec des scores prédéfinis.
Arbre de recherche
Nœud racine : Représente l’état initial avant le coup du Joueur 1.
Ply 1 : Le Joueur 1 choisit entre les coups \(A\) et \(B\).
Ply 2 : Pour chaque coup du Joueur 1, le Joueur 2 choisit entre les coups \(C\) et \(D\).
Nœuds feuilles : Le point final de chaque branche est un état terminal avec un score associé.
Scores
\((A, C)\) résulte en un score de 3.
\((A, D)\) résulte en un score de 5.
\((B, C)\) résulte en un score de 2.
\((B, D)\) résulte en un score de 1.
Stratégie
Stratégie
Stratégie
Stratégie
Minimax
Le Joueur 1 est le joueur maximisateur, cherchant à obtenir le score le plus élevé.
Le Joueur 2 est le joueur minimisateur, cherchant à obtenir le score le plus bas.
Évaluation :
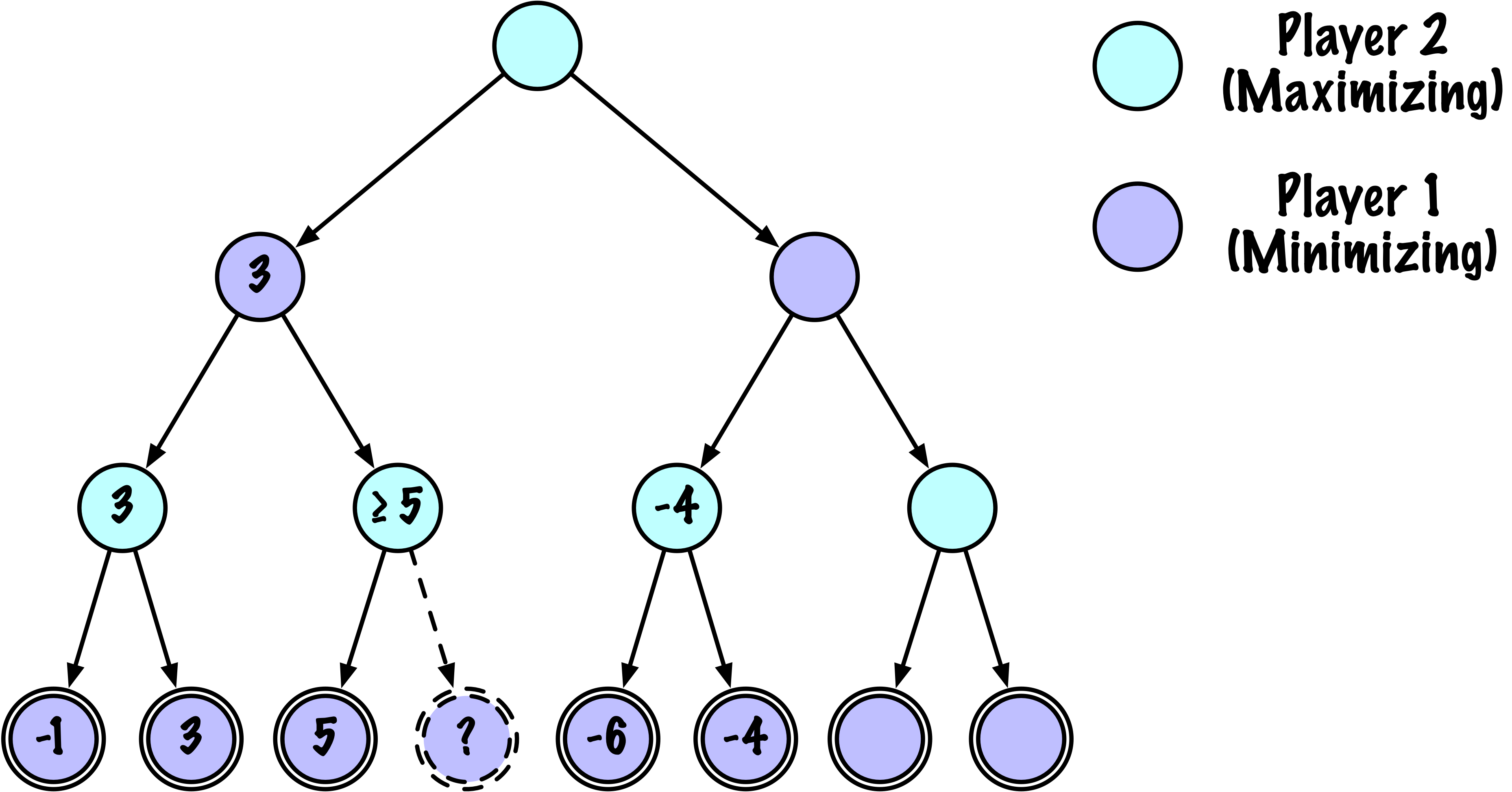
Le Joueur 2 évalue les résultats potentiels pour chacun de ses coups et choisit le résultat le moins favorable pour le Joueur 1.
Le Joueur 1 évalue ensuite ces résultats, choisissant le coup qui maximise son score minimum garanti.
Recherche Minimax
Recherche Minimax
L’algorithme minimax fonctionne en explorant tous les coups possibles dans un arbre de jeu, en évaluant les résultats pour minimiser la perte possible dans le pire des cas. À chaque nœud :
Tour du joueur maximisateur : Choisir le coup avec la valeur la plus élevée possible.
Tour du joueur minimisateur : Choisir le coup avec la valeur la plus basse possible.
En remontant des nœuds terminaux à la racine, l’algorithme sélectionne le coup qui maximise le gain minimum du joueur, anticipant efficacement et contrant les meilleures stratégies de l’adversaire.
Recherche Minimax
Présentation (premières 4 minutes)
Base
Tic-Tac-Toe
# Classe de jeu Tic-Tac-Toe
class TicTacToe(Game):
def __init__(self):
self.size = 3
self.board = np.full((self.size, self.size), ' ')
def get_valid_moves(self, state):
# Retourne une liste des positions disponibles
moves = []
for i in range(self.size):
for j in range(self.size):
if state[i][j] == ' ':
moves.append((i, j))
return moves
def make_move(self, state, move, player):
# Retourne un nouvel état après avoir effectué le coup
new_state = state.copy()
new_state[move] = player
return new_state
def is_terminal(self, state):
# Vérifie les lignes, les colonnes et les diagonales pour une victoire
lines = []
lines.extend(state) # Lignes
lines.extend(state.T) # Colonnes
lines.append(np.diagonal(state)) # Diagonale principale
lines.append(np.diagonal(np.fliplr(state))) # Anti-diagonale
for line in lines:
if np.all(line == 'X') or np.all(line == 'O'):
return True
# Vérifie s'il y a un match nul (pas d'espaces vides)
if ' ' not in state:
return True
return False
def evaluate(self, state):
# Fonction d'évaluation simple
lines = []
lines.extend(state) # Lignes
lines.extend(state.T) # Colonnes
lines.append(np.diagonal(state)) # Diagonale principale
lines.append(np.diagonal(np.fliplr(state))) # Anti-diagonale
for line in lines:
if np.all(line == 'X'):
return 1 # X gagne
if np.all(line == 'O'):
return -1 # O gagne
return 0 # Match nul ou en cours
def display(self, state):
display_tic_tac_toe(state, title=None)
def get_opponent(self, player):
return 'O' if player == 'X' else 'X'Minimax
import math
def minimax(game, state, depth, player, maximizing_player):
if game.is_terminal(state) or depth == 0:
return game.evaluate(state), None
valid_moves = game.get_valid_moves(state)
best_move = None
if maximizing_player:
max_eval = -math.inf
for move in valid_moves:
new_state = game.make_move(state, move, player)
eval_score, _ = minimax(game, new_state, depth - 1, game.get_opponent(player), False)
if eval_score > max_eval:
max_eval = eval_score
best_move = move
return max_eval, best_move
else:
min_eval = math.inf
for move in valid_moves:
new_state = game.make_move(state, move, player)
eval_score, _ = minimax(game, new_state, depth - 1, game.get_opponent(player), True)
if eval_score < min_eval:
min_eval = eval_score
best_move = move
return min_eval, best_moveExécution
def test_tic_tac_toe():
game = TicTacToe()
current_state = game.board.copy()
player = 'X'
maximizing_player = True
# Simuler une partie
while not game.is_terminal(current_state):
game.display(current_state)
_, move = minimax(game, current_state, depth=9, player=player, maximizing_player=maximizing_player)
if move is None:
print("Fin de la partie !")
break
current_state = game.make_move(current_state, move, player)
player = game.get_opponent(player)
maximizing_player = not maximizing_player
game.display(current_state)
result = game.evaluate(current_state)
if result == 1:
print("X gagne !")
elif result == -1:
print("O gagne !")
else:
print("C'est un match nul !")Exécution (1/2)
Exécution plus rapide (digression)
test_tic_tac_toeest-il plus lent que prévu ?Voyez-vous un domaine à améliorer ?
Cache
def memoize_minimax(f):
cache = {}
def wrapper(game, state, depth, player, maximizing_player):
state_key = tuple(map(tuple, state)) # état hachable
key = (state_key, depth, player, maximizing_player)
if key in cache:
return cache[key]
result = f(game, state, depth, player, maximizing_player)
cache[key] = result
return result
return wrapperCache
@memoize_minimax
def minimax(game, state, depth, player, maximizing_player):
# Le code minimax reste le même, sans gestion de cache
if game.is_terminal(state) or depth == 0:
return game.evaluate(state), None
valid_moves = game.get_valid_moves(state)
best_move = None
if maximizing_player:
max_eval = -math.inf
for move in valid_moves:
new_state = game.make_move(state, move, player)
eval_score, _ = minimax(game, new_state, depth - 1, game.get_opponent(player), False)
if eval_score > max_eval:
max_eval = eval_score
best_move = move
return max_eval, best_move
else:
min_eval = math.inf
for move in valid_moves:
new_state = game.make_move(state, move, player)
eval_score, _ = minimax(game, new_state, depth - 1, game.get_opponent(player), True)
if eval_score < min_eval:
min_eval = eval_score
best_move = move
return min_eval, best_moveExécution (2/2)
Réduire la prévisibilité (digression)
import random
class TicTacToe(Game):
def get_valid_moves(self, state):
# Retourne une liste des positions disponibles
moves = []
for i in range(self.size):
for j in range(self.size):
if state[i][j] == ' ':
moves.append((i, j))
return random.shuffle(moves)
# Toutes les autres méthodes restent les mêmesExploration
Comparez la réduction du temps d’exécution obtenue grâce aux considérations de symétrie par rapport aux techniques de mise en cache. Évaluez l’effet combiné des deux approches.
Développez une implémentation du jeu Puissance 4 (Connect 4) utilisant un algorithme de recherche minimax.
Le Puissance 4 (Connect 4) est symétrique par rapport à son axe vertical. Développez une nouvelle implémentation qui exploite cette symétrie.
Remarque
Le nombre de séquences valides d’actions croît de manière factorielle, avec une croissance particulièrement importante observée dans les jeux comme les échecs et le Go.
Élagage
Pour améliorer l’efficacité de l’algorithme minimax, on pourrait éventuellement élaguer certaines parties de l’arbre de recherche, évitant ainsi l’exploration des nœuds descendants.
Élagage
Comment mettriez-vous en œuvre cette modification ? Quels facteurs prendriez-vous en compte ?
Élagage
L’élagage de l’arbre doit être effectué uniquement lorsqu’il peut être démontré que ces sous-arbres ne peuvent pas fournir de meilleures solutions.
Critères pour l’élagage
Critères pour l’élagage
Critères pour l’élagage
Critères pour l’élagage
Critères pour l’élagage
Critères pour l’élagage
Critères pour l’élagage
Critères pour l’élagage
Critères pour l’élagage
Critères pour l’élagage
Critères pour l’élagage
Critères pour l’élagage
Critères pour l’élagage
Critères pour l’élagage
Critères pour l’élagage
Critères pour l’élagage
Élagage Alpha-Bêta
L’élagage alpha-bêta est une technique d’optimisation pour l’algorithme minimax qui réduit le nombre de nœuds évalués dans l’arbre de recherche.
Élagage Alpha-Bêta
Il y parvient en éliminant les branches qui ne peuvent pas influencer la décision finale, en utilisant deux paramètres :
alpha, le score maximum que le joueur maximisateur est assuré d’obtenir, et
bêta, le score minimum que le joueur minimisateur est assuré d’obtenir.
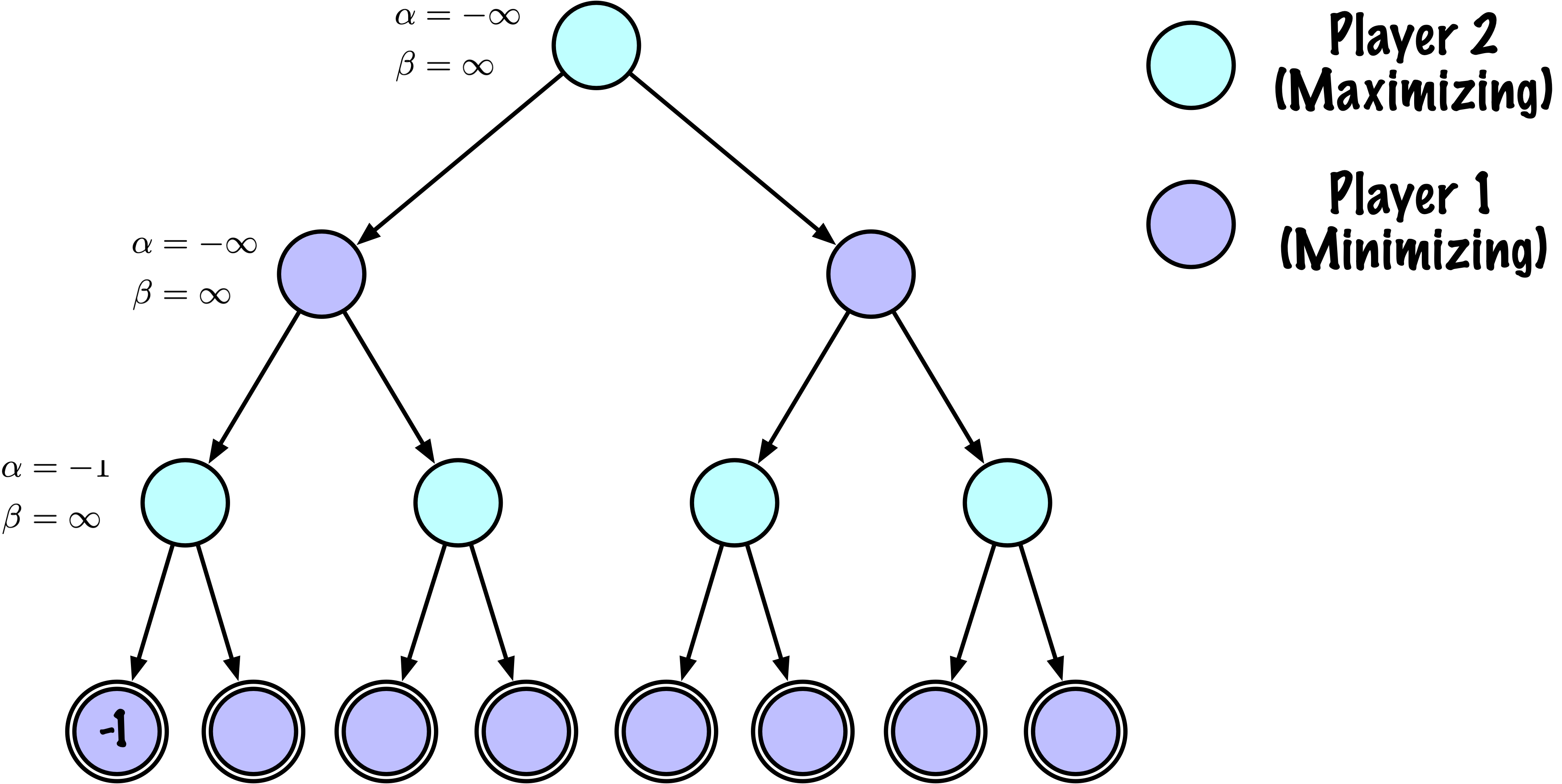
Perspective du joueur maximisateur
À un nœud maximisateur :
Le maximiseur vise à maximiser le score.
Alpha (\(\alpha\)) est mis à jour avec la valeur la plus élevée trouvée jusqu’à présent parmi les nœuds enfants.
Processus :
Initialiser \(\alpha = -\infty\).
Pour chaque nœud enfant :
Calculer le score d’évaluation.
Mettre à jour \(\alpha = \max(\alpha, \mathrm{score\_enfant})\).
Perspective du joueur minimisateur
À un nœud minimisateur :
Le minimiseur vise à minimiser le score.
Bêta (\(\beta\)) est mis à jour avec la valeur la plus basse trouvée jusqu’à présent parmi les nœuds enfants.
Processus :
Initialiser \(\beta = \infty\).
Pour chaque nœud enfant :
Calculer le score d’évaluation.
Mettre à jour \(\beta = \min(\beta, \mathrm{score\_enfant})\).
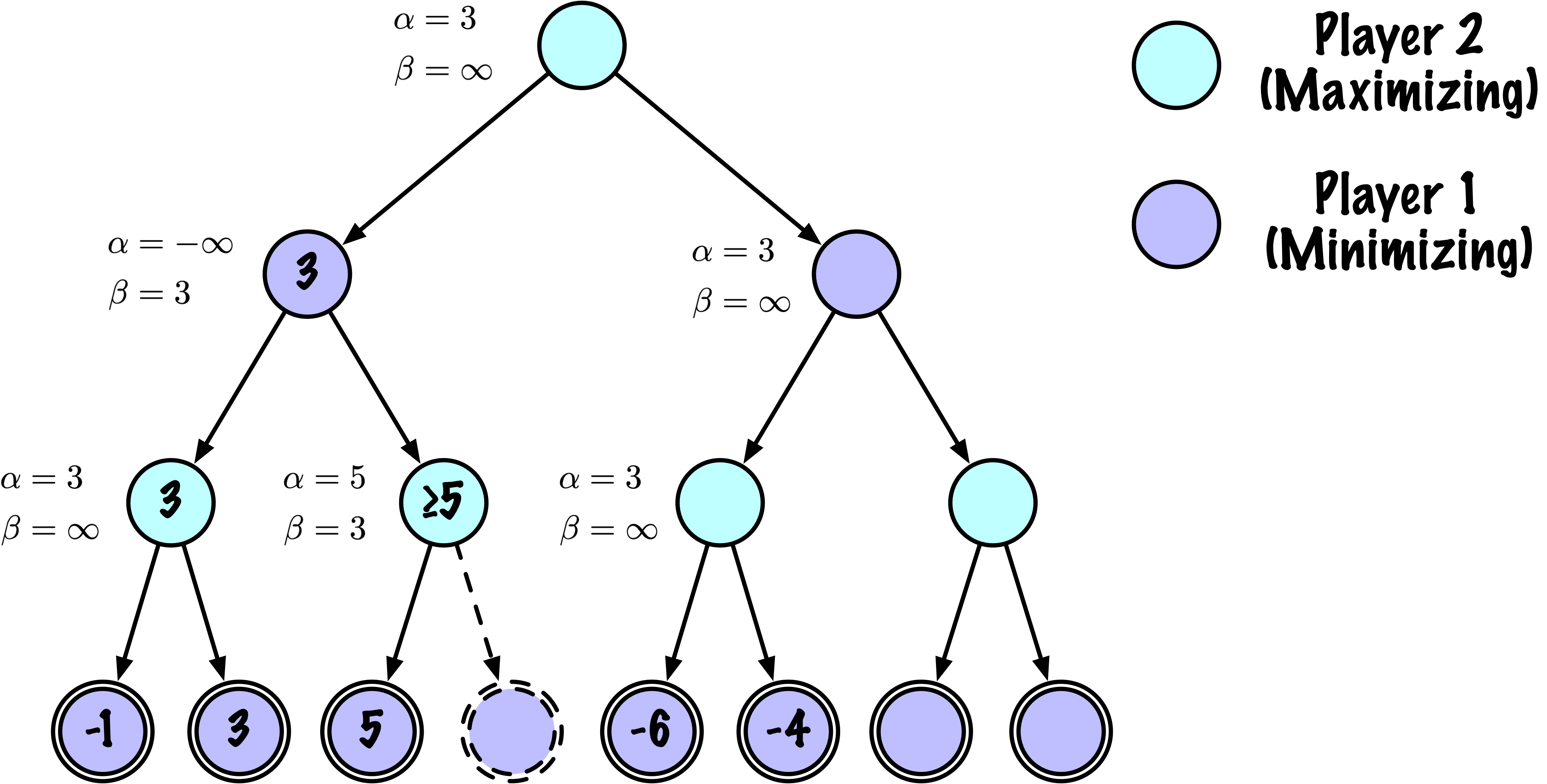
Élagage Alpha-Bêta
Lorsque l’évaluation d’un nœud prouve qu’il ne peut pas améliorer l’alpha ou le bêta actuels, l’exploration de cette branche est arrêtée, ce qui améliore l’efficacité computationnelle sans affecter le résultat.
Rôle d’Alpha et Bêta dans l’élagage
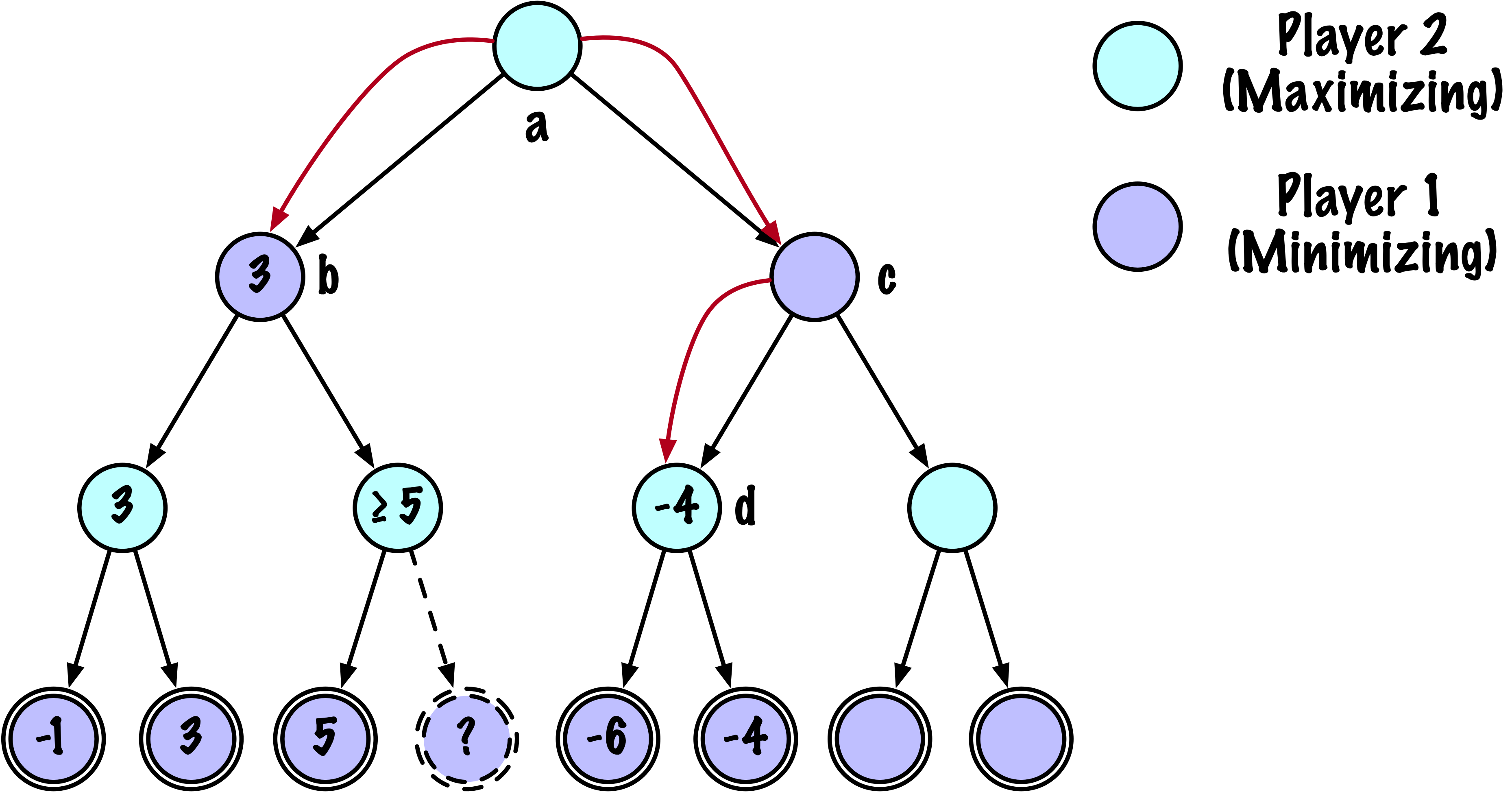
Condition d’élagage :
Si \(\beta \leq \alpha\), l’exploration supplémentaire des nœuds frères actuels est inutile.
Raisonnement :
Le maximiseur a un score garanti d’au moins \(\alpha\).
Le minimiseur peut s’assurer que le maximiseur ne peut pas obtenir un meilleur score que \(\beta\).
Si \(\beta \leq \alpha\), le maximiseur ne trouvera pas de meilleure option dans cette branche.
Recherche Alpha-Bêta
Présentation (6:21 à 8:10)
Ordre des nœuds
L’efficacité de l’élagage est influencée par l’ordre dans lequel les nœuds sont évalués.
Un élagage plus important est réalisé si les nœuds sont ordonnés du plus prometteur au moins prometteur.
Recherche Alpha-Bêta
# Algorithme Minimax avec élagage Alpha-Bêta
def alpha_beta_search(game, state, depth, player, alpha, beta, maximizing_player):
"""
Algorithme Minimax avec élagage alpha-bêta.
:param game: L'instance du jeu.
:param state: L'état actuel du jeu.
:param depth: La profondeur maximale de recherche.
:param player: Le joueur actuel ('X' ou 'O').
:param alpha: La meilleure valeur que le maximiseur peut garantir à ce niveau ou au-dessus.
:param beta: La meilleure valeur que le minimiseur peut garantir à ce niveau ou au-dessus.
:param maximizing_player: Vrai si le coup actuel est pour le maximiseur.
:return: Un tuple de (score d'évaluation, meilleur coup).
"""Recherche Alpha-Bêta
Recherche Alpha-Bêta
if maximizing_player:
max_eval = -math.inf # Initialiser l'évaluation maximale
for move in valid_moves:
# Simuler le coup
new_state = game.make_move(state, move, player)
# Appel récursif à alpha_beta_search pour le joueur minimiseur
eval_score, _ = alpha_beta_search(game, new_state, depth - 1, game.get_opponent(player), alpha, beta, False)
if eval_score > max_eval:
max_eval = eval_score # Mettre à jour l'évaluation maximale
best_move = move # Mettre à jour le meilleur coup
alpha = max(alpha, eval_score) # Mettre à jour alpha
if beta <= alpha:
break # Coupure bêta (élaguer les branches restantes)
return max_eval, best_moveRecherche Alpha-Bêta
else:
min_eval = math.inf # Initialiser l'évaluation minimale
for move in valid_moves:
# Simuler le coup
new_state = game.make_move(state, move, player)
# Appel récursif à alpha_beta_search pour le joueur maximisateur
eval_score, _ = alpha_beta_search(game, new_state, depth - 1, game.get_opponent(player), alpha, beta, True)
if eval_score < min_eval:
min_eval = eval_score # Mettre à jour l'évaluation minimale
best_move = move # Mettre à jour le meilleur coup
beta = min(beta, eval_score) # Mettre à jour bêta
if beta <= alpha:
break # Coupure alpha (élaguer les branches restantes)
return min_eval, best_movePrésentation
Présentation
Présentation
Présentation
Présentation
Présentation
Présentation
Présentation
Présentation
Présentation
Présentation
Présentation
Résumé
Coupe alpha : Se produit aux nœuds minimiseurs lorsque \(\beta \le \alpha\).
Coupe bêta : Se produit aux nœuds maximiseurs lorsque \(\alpha \ge \beta\).
Minimax vs Élagage Alpha-Bêta
Comprendre pourquoi l’élagage alpha-bêta améliore l’efficacité du minimax sans modifier les résultats nécessite une réflexion attentive.
Les changements de l’algorithme sont minimes.
L’amélioration est-elle justifiée ?
Minimax vs Élagage Alpha-Bêta
Nombre de séquences explorées par l'algorithme de recherche Minimax : 255,168
Nombre de séquences explorées par l'algorithme de recherche Alpha-Bêta : 7,330
Une réduction de 97.13% du nombre de séquences visitées !Exploration
Implémentez un jeu de Puissance 4 (Connect 4) en utilisant l’algorithme de recherche Alpha-Bêta. Réalisez une analyse comparative entre les implémentations de Minimax et de recherche Alpha-Bêta.
Prologue
Exploration supplémentaire
Recherche Expetimax : gérer les joueurs qui ne sont pas parfaits ;
Expectiminimax : gérer le hasard dans des jeux tels que le backgammon.
Résumé
- Introduction à la recherche en environnement adversarial
- Jeux à somme nulle
- Introduction à la méthode de recherche minimax
- Rôle de l’élagage alpha et bêta dans la recherche minimax
Prochain cours
- Nous aborderons l’algorithme de recherche arborescente Monte Carlo (MCTS)
Références
Marcel Turcotte
École de science informatique et de génie électrique (SIGE)
Université d’Ottawa