[ PDF ]
Proteins are large molecules that participate in virtually all cellular processes. Their three-dimensional structure is closely related to their function. So much so that protein misfolding often result in diseases. For instance, Parkinson’s and Alzheimer’s diseases are believed to be the result of protein misfolding. Consequently, in order to assist fundamental life science research, computational methods for predicting the three-dimensional structure of proteins are highly sought.
Computational approaches to protein folding require large computing resources. For example, a group of scientists at Stanford University (Folding@home) has created an application (client) that people can download and run on their personal computer and Sony PlayStation 3 to dedicate free CPU cycles to their project.
Proteins are three-dimensional objects, but simplified two dimensional models are sometimes used to either study the behavior of algorithms or properties of mathematical models. Here, in order to reduce both the complexity of the assignment and the execution time, we study the protein folding problem using a lattice representation and the hydrophobic-polar protein folding model. For this assignment, a protein is a chain made two types of constituents, hydrophobic (h) and polar (p) on a two-dimensional grid.
For a given input chain made of the types of constituents, h or p, find a two dimensional representation such that 1) no two constituents overlap and 2) the number non-contiguous hydrophobic constituents in the chain that are adjacent in the grid is maximum.
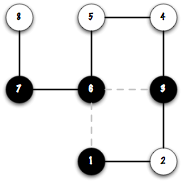
Here is an example where the folded chain “hphpphhp” makes two hydrophobic contacts. Hydrophobic and polar constituents are represented by black and white circles, respectively. Constituent that are contiguous in the chain are connected by a solid line, whilst non-contiguous hydrophobic contacts are represented by dashed lines. This example will be used throughout the text.

Some problems have no known algorithm that is both exact and efficient. By exact, we mean an algorithm that finds the “true” answer to the given problem. For example, in the case of a minimization (optimization) problem, the algorithm must find the solution with the highest value. By efficient, we mean an algorithm that can be applied to interesting, real-world, data sets, and takes a reasonable amount of time to run (32,000 years is not a reasonable amount of time).
There are many such problems that need to be solved. The most famous one is probably the “Travelling salesman problem”, which seeks to find the least-cost round-trip itinerary that visits each city exactly once and returns to the starting city, given n cities and the cost of travelling from any city to any city.
Because answers to these problems are needed, approximate solutions are sought that can be found in reasonable amounts of time. Genetic Algorithms (GAs), a.k.a. Evolutionary Computing, are a family of approaches for finding approximate solutions for a variety of challenging problems.
GAs borrow several concepts from natural selection. Briefly, the approach consists of generating an initial population of candidate solutions. These solutions are generally generated randomly. Consequently, the quality of the initial solutions is low. The algorithm then creates new generations of the population by (randomly) selecting individuals to reproduce (through crossover and mutation operators, see Chromosome for further information). The new individual with the highest fitness value replaces the element of the population with the lowest one. Hence, improving the average fitness of the population. The algorithm stops when the maximum number of generations has been reached. The best individual is returned as a solution to the initial problem.
For this assignment, you must implement a genetic algorithm that solves the protein folding problem described above. You must use the provided template classes below. Each template contains further information for solving the problem.
Follow all the directives available on the assignment directives web page, and submit your assignment through the on-line submission system Blackboard Learn.
You must preferably do the assignment in teams of two, but you can also do the assignment individually. Pay attention to the directives and answer all the following questions.
We will represent the fold of the protein as a series of moves on a two dimensional lattice. Therefore, the above fold (diagram) for the chain “hphpphhp” is represented by the following moves: Right, Up, Up, Left, Down, Left, Up. For a chain of length n, its fold is represented by n - 1 moves, which you can think of as the links between the constituents.
The class Folding implements the top level of the algorithm. It has a main method that reads the chain from the command line. Here is a sample run.
Because of the “probabilistic” nature of the algorithm, each run is likely to produce a different solution.
The assignment has three main classes, Folding, Population and Chromosome. The static method solve of the class Folding implements the top level of the algorithm. It first creates a Population of solutions (objects of the class Chromosome). Next, it repeatedly calls the method evolve of the population. Finally, it returns the “fittest” individual.
A Population has a collection of candidate solutions (objects of the class Chromosome). When the method evolve is called, two parents solutions are selected and used to create a child solution. The child is inserted into the population and the chromosome with the lowest fitness value removed.
A Chromosome is a candidate solution. It consists of n genes. In our case, the genes are moves on a two dimensional grid. When a chromosome is first created, the value of the genes are randomly selected. The fitness of a chromosome is a measure of the quality of the solution that it represents. For our problem, the fitness depends on the number of (good) hydrophobic contacts and the number of (bad) overlapping constituents. A chromosome has a method crossOver that takes an input another chromosome and returns a new child chromosome, which is the crossover between this and the other chromosome. Consult the template for further information.
Move is an enumerated type representing all four possible moves on a two dimensional grid. Use this for the type of the genes in the Chromosome class.
A Chromosome is a candidate solution. Its representation depends on the specific problem to be solved. Two chromosomes can be combined (see method crossover) to produce a new offspring. As with natural chromosomes, these artificial ones suffer mutations. Each chromosome has a fitness value that indicates the quality of this solution. A Population is a collection of chromosomes. At each iteration (generation), the genetic algorithm selects chromosomes for reproduction. Their offspring are inserted into the population, and the least fitted individuals are eliminated. The size of the population is fixed.
A detailed description of the class Chromosome can be found in the JavaDoc Documentation.
As mentioned above, a Population is a collection of chromosomes (each one representing a candidate solution for the folding problem). To facilitate the implementation of the various methods, the chromosomes will always be kept in increasing value of fitness.
A detailed description of the class Chromosome can be found in the JavaDoc Documentation.
Complete the implementation of the method private static Chromosome solve( String chain ). It creates a new population, does NUMBER_OF_GENERATIONS rounds of evolution, and returns the fittest individual.
A detailed description of the class Chromosome can be found in the JavaDoc Documentation.
In a file, named best.txt, write down your best solution for the chain “hphpphhphpphphhpphph”.
This part of the assignment is meant to raise awareness concerning plagiarism and academic fraud. Please read the following two documents.
Cases of plagiarism will be dealt with according to the university regulations.
By submitting this assignment, you acknowledge:
You must hand in the following files.
The following two files are related to the (optional) user interface.
Indeed, calculating the fitness value is one of the challenges of this assignment.
Each chromosome object represents a solution for the folding problem. In particular, each object Chromosome has an attribute chain to store the input chain (e.g. “hphhphhph”), as well as an attribute to store the sequence of moves represented by this solution (e.g. Move.Right, Move.Up, Move.Left, Move.Down, Move.Down, Move.Left, Move.Up, Move.Right). There might be other attributes as well.
Given this information, how can you calculate the fitness of the solution?
Recall that the fitness of a solution is defined as follows:
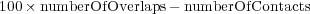
I suggest dividing the calculation into two sub-tasks: counting overlaps and counting contacts.
Given a sequence of moves, how can you calculate the number of overlapping constituents? In other words, given Move.Right, Move.Up, Move.Left, Move.Down, Move.Down, Move.Left, Move.Up, Move.Right, how can you determine that there are three overlaps?
The problem is the representation. The sequence of moves is useful for the methods crossover and mutate, but not for getFitness.
One way around this problem is to create a temporary representation when computing the fitness value. A natural representation would be one that looks like the drawings that I made in class.
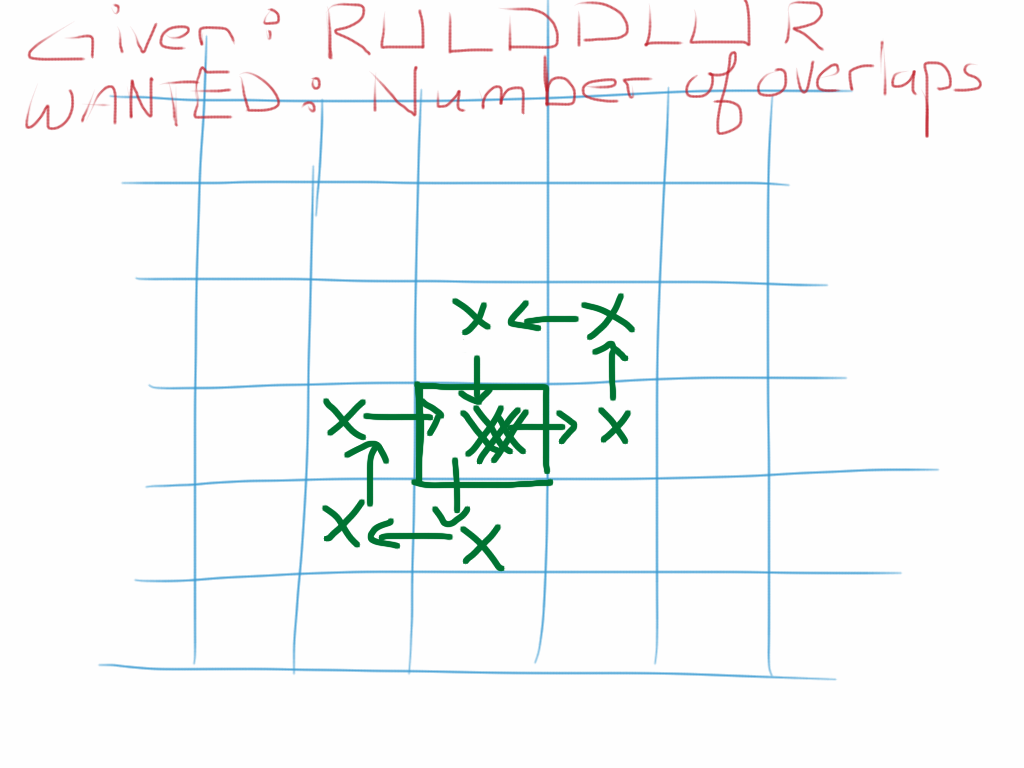
You should be able to process the sequence of moves, Move.Right, Move.Up, Move.Left, Move.Down, Move.Down, Move.Left, Move.Up, Move.Right, so as to write useful information into that temporary data structure (representation). What should be the type of the element in each cell in order to count overlaps?
Once you have solved that problem, you should consider counting the number of contacts. A similar temporary representation will be useful. This time, counting the number of times a cell has been visited will not be enough. What kind of information would be useful in order to determine the number of contacts?
No! Consult directives page, and create a .jar file, as explained therein.
The rule is simple, you cannot add public methods or variables; this would affect the interface of the class. However, you can add private methods to help you solve a problem. In fact, you are encouraged to create such methods to improve the structure of your programs.
Before Java 1.5, we used to use integer constants to represent symbolic constants, such as the day of the week or the month of the year.
However, as the obove example shows, since all the constants were integers, the compiler would not be able to detect error situations where a symbolic constant representing a month would be assigned to a variable representing a day of the week.
Java 1.5 introduced enumerated types that allow for the same kind of constructions, but in a typesafe way.
If the above code is changed to include the following line.
Then the following error message will be displayed at compile-time.
Here are complementary informations:
No. We will handle error situations once we have seen the concept of exceptions.
No! The random number generator (Math.random()) has a finite number of values to choose from, say N, where N is a very large
number since double precision floating-point numbers are used. These values are in the range 0.0 to 1.0. The probability that the
randomly generated number equals x, where x = 0.8 for instance, is 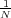 ; this is one of the N possible outcomes. Therefore, the
probability that the random number generator produces the value x is
; this is one of the N possible outcomes. Therefore, the
probability that the random number generator produces the value x is 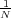 , which is a very small number (close to
zero).
, which is a very small number (close to
zero).
Here is how you should look at the problem. Math.random() randomly selects one of the N possible values (from the range 0.0 to
1.0). All the values have the same probability of being selected (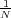 ). We also say that the probability distribution is approximately
uniform. If one makes a very large number of calls to the method Math.random(), one would expect the values to be uniformly
distributed in the interval 0.0 to 1.0, with 100% of the values being less than or equals to 1.0, 95% of the values less than or
equals to 0.95, 90% of the values will be less than or equals to 0.90, etc. Here is a small program to illustrate
that.
). We also say that the probability distribution is approximately
uniform. If one makes a very large number of calls to the method Math.random(), one would expect the values to be uniformly
distributed in the interval 0.0 to 1.0, with 100% of the values being less than or equals to 1.0, 95% of the values less than or
equals to 0.95, 90% of the values will be less than or equals to 0.90, etc. Here is a small program to illustrate
that.
First, the assignment does not say that you should use a sort method, my implementation certainly does not, the description says that “chromosomes will always be kept in increasing value of fitness”.
If you were to use a method sort, which would also lead to a slower implementation, then yes you can use the sort method from the API.
Yes, you need to implement all the methods. You should see the assignment as a specification, and therefore need to implement all the specified methods. But also, these methods will be used by our automated test procedures.
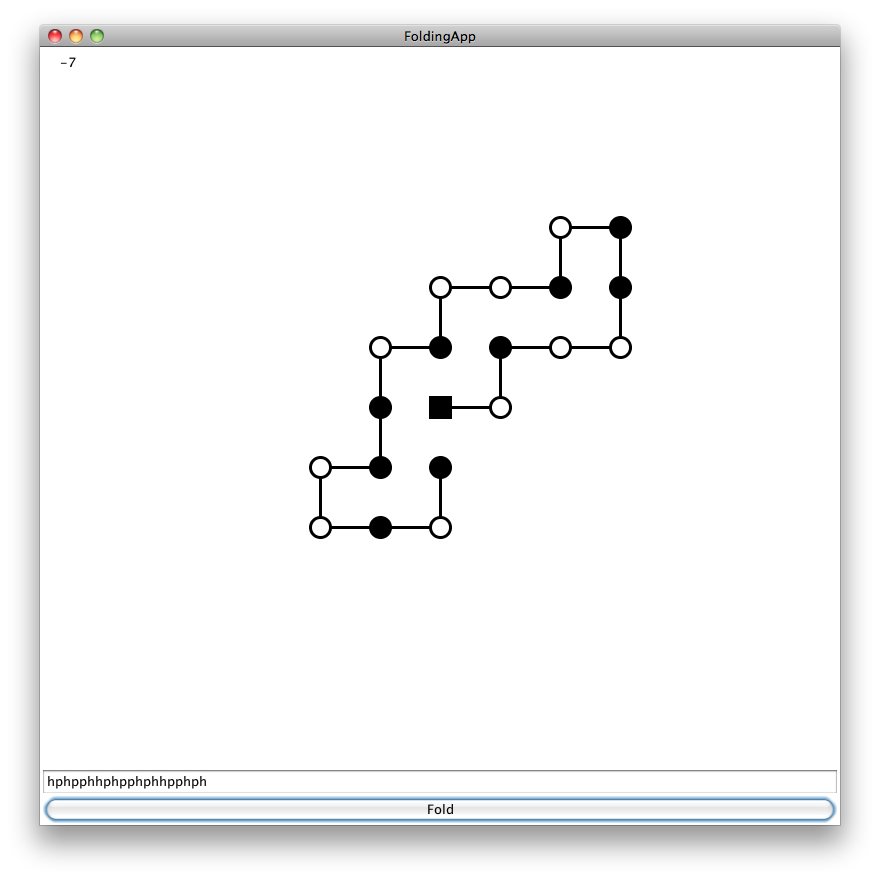
In order to facilitate testing and debugging your application, I created a simple user interface where you can type in your chain and visualize the best solution that your program can find.
Last Modified: February 8, 2013