[ PDF ]
Les protéines sont de grosses molécules qui participent à un grand nombre de processus cellulaires. Leur structure tridimensionnelle et leur fonction sont intimement liées de sorte que des erreurs de repliement sont souvent la cause de maladies. Par exemple, ça semble être le cas pour les maladies de Parkinson et Alzheimer. Ainsi, des méthodes informatiques pour prédire le repliement des protéines sont nécessaires pour assister les recherches en science de la vie.
Les approches informatiques pour le repliement de protéines demandent de grandes ressources informatiques. Par exemple, un groupe de chercheurs de l’Université Stanford (Folding@home) a créé une application (client) que les gens peuvent télécharger et faire tourner sur leurs ordinateurs personnels et consoles de jeu Sony PlayStation 3 afin de partager leur capacité de calcul avec ces chercheurs.
Les protéines sont des objets tridimensionnels, mais on utilise parfois des modèles simplifiés à deux dimensions afin d’étudier le comportement des algorithmes ou les propriétés des modèles mathématiques. Afin de réduire la taille et complexité du devoir, ainsi que les temps d’exécution, nous étudierons le problème de repliement à l’aide de treillis à deux dimensions et du modèle hydrophobe-polaire. Pour ce devoir, une protéine est une chaîne ayant deux types de constituants, hydrophobe (h) et polaire (p), que l’on replie sur une grille à deux dimensions.
Étant donné une chaîne en entrée formée de constituants de type h ou b, trouvez une représentation en deux dimensions telle que 1) les constituants n’occupent pas les mêmes positions et 2) le nombre de constituants hydrophobes adjacents sur la grille, mais non contigus dans la chaîne, est maximum.
Voici un exemple de repliement pour la chaîne ≪ hphpphhp ≫. Les constituants hydrophobes et polaires sont représentés à l’aide de cercles noirs et blancs, respectivement. Les constituants qui sont contigus dans la chaîne sont connectés les uns aux autres à l’aide de lignes pleines, alors que les contacts hydrophobes sont représentés à l’aide de traits pointillés. Cet exemple sera utilisé dans la suite du texte.
Pour certains problèmes, il n’y aucun algorithme exact et efficace connu. Exact signifie un algorithme qui trouve la ≪ vraie ≫ solution au problème donné. Par exemple, pour un problème de minimisation (optimisation), l’algorithme doit trouver une solution dont la valeur est inférieure à la valeur de toutes autres solutions. Efficace signifie un algorithme qui peut traiter des jeux de données intéressants, de taille réelle, dans un temps raisonnable (personne ne veut attendre 32,000 ans pour obtenir une solution).
La résolution de tels problèmes est bien souvent nécessaire. Le problème de ce genre le mieux connu est sans doute le problème du commis voyageur (≪ travalling salesman problem ≫). Étant donné n villes ainsi que les coûts de déplacement d’une ville à l’autre, il s’agit de trouver un chemin de moindre coût visitant chaque ville exactement une fois, puis qui retourne à la ville de départ.
Puisque les solutions de tels problèmes sont nécessaires, on se contente souvent de solutions approchées que l’on peut trouver en un temps raisonnable. Les algorithmes génétiques (GAs) sont une famille d’approches pour trouver des solutions approchées pour un grand nombre de problèmes difficiles à résoudre.
Les algorithmes génétiques s’inspirent du processus de sélection naturelle. En résumé, l’approche consiste à générer une population initiale de solutions. Elles sont généralement générées au hasard. Par conséquent, la qualité des solutions initiales est généralement médiocre. Par la suite, l’algorithme génère de nouvelles populations en sélectionnant (au hasard) des parents qui produiront (par croisement et mutations) une solution enfant. Les solutions mieux adaptées (de meilleure qualité) remplaceront les solutions inférieures afin d’augmenter la performance moyenne de la population. L’algorithme s’arrête après un nombre fixe et prédéterminé de générations (itérations). À la fin, l’individu ayant la meilleure performance est retourné.
Pour ce devoir, vous devez implémenter un algorithme génétique afin de résoudre le problème du repliement des protéines décrit ci-haut. Vous devez utiliser les classes modèles décrites ci-dessous. Chaque modèle contient des informations supplémentaires afin de résoudre le problème.
Veuillez suivre les consignes disponibles sur la page des consignes aux devoirs. Tous les devoirs doivent être soumis à l’aide de maestro.
Vous devez préférablement faire le travail en équipe de deux, mais vous pouvez aussi faire le travail individuellement.
Nous représenterons le repliement d’une protéine à l’aide d’une série de déplacements sur une grille à deux dimensions. Ainsi, le repliement (diagramme) ci-haut pour la chaîne “hphpphhp” sera représenté par les déplacements suivant : Right, Up, Up, Left, Down, Left, Up. Pour une chaîne de longueur n, son repliement comprend n - 1 déplacements.
La classe Folding comprend la boucle principale de cet algorithme. Cette classe possède aussi une méthode principale qui utilise la ligne de commandes pour obtenir l’entrée du programme.
Étant donné la nature ≪ probabiliste ≫ de l’algorithme, chaque exécution produira une solution différente.
Ce devoir possède 3 classes principales, Folding, Population et Chromosome. La méthode de classe solve de la classe Folding implémente la boucle principale de l’algorithme. Cette méthode devra tout d’abord créer une nouvelle Population de solutions (des objets de la classe Chromosome). Ensuite, elle fera des appels répétés à la méthode evolve de la population. Finalement, elle retourne la meilleure solution trouvée.
Une Population possède une collection de solutions (objets de la classe Chromosome). Lors d’un appel à la méthode evolve, deux parents sont sélectionnés et utilisés afin de créer une solution enfant. Cette nouvelle solution est insérée dans la population et le chromosome ayant la pire valeur d’adaptation est retiré de la population.
Un Chromosome est une solution au problème. Il comprend n gènes. Pour ce devoir, les valeurs des gènes sont des déplacements sur une grille à deux dimensions. Lorsqu’un chromosome est créé, les valeurs des gènes sont choisies aléatoirement. La valeur d’adaptation (≪ fitness ≫) d’un chromosome mesure la qualité de la solution. Pour ce devoir, la valeur d’adaptation dépend à la fois du nombre de contacts hydrophobes (bonus) et du nombre de recouvrements (pénalités). Un chromosome possède une méthode d’instance crossOver qui prend en entrée un autre chromosome et retourne un nouveau chromosome enfant, qui est le résultat du croisement entre ce chromosome et celui fourni en entrée. Consultez les classes modèles pour des informations complémentaires.
Move est un type énuméré représentant les quatre déplacements possibles dans un espace à deux dimensions. Utilisez le pour le type des gènes de la classe Chromosome.
Un Chromosome représente une solution au problème. Sa représentation dépend du problème à résoudre. Deux chromosomes parents servent à produire un chromosome enfant (voir méthode crossOver). Comme les chromosomes naturels, ces chromosomes artificiels subissent des mutations. Chaque chromosome possède une valeur d’adaptation (fitness) qui représente la qualité de la solution. Une Population possède une collection de chromosomes. Pour chaque itération, l’algorithme génétique choisi des parents qui servent à produire des solutions enfants. Ces enfants sont insérés dans la population, et les individus les moins bien adaptés sont retirés. Ainsi, la taille de la population demeure fixe.
Une description détaillée de la classe Chromosome se trouve dans le JavaDoc.
Comme nous l’avons vu, une Population comprend une collection de chromosomes (chacun représente une solution distincte au problème de repliement). Pour faciliter l’implémentation des méthodes de cette classe, les chromosomes sont sauvegardés en ordre croissant de leur valeur d’adaptation.
Une description détaillée de cette classe se trouve dans le JavaDoc.
Complétez l’implémentation de la méthode de classe solve. Elle crée une nouvelle population, exécute NUMBER_OF_GENERATIONS itérations, pour finalement retourner la meilleure solution trouvée.
Une description détaillée de cette classe se trouve dans le JavaDoc.
Dans un fichier texte, nommé best.txt, sauvegardez la meilleure solution trouvée pour la chaîne ≪ hphpphhphpphphhpphph ≫.
Cette partie du devoir a pour but de sensibiliser les étudiants face au problème de fraude scolaire (plagiat). Lisez les deux documents qui suivent
Les règlements de l’université seront appliqués pour tout cas de plagiat.
En soumettant ce devoir :
Vous devez soumettre les fichiers suivants :
Ces deux fichiers font partie de l’interface usager (optionnelle).
En effet, le calcul de la valeur d’adaptation est l’un des défis de ce devoir.
Chaque chromosome (objet) représente un repliement possible de la chaîne donnée en entrée. En particulier, chaque objet (Chromosome) possède un attribut chaîne afin de sauvegarder la chaîne donnée en entrée (p.e. “hphhphhph”), ainsi qu’un attribut pour sauvegarder la séquence de déplacements représentée par cette solution (p.e. Move.Right, Move.Up, Move.Left, Move.Down, Move.Down, Move.Left, Move.Up, Move.Right). Il se peut qu’il y ait d’autres attributs.
Étant donné ces informations, comment peut-on calculer la valeur d’adaptation (fitness) ?
Souvenez-vous que la valeur d’adaptation d’une solution est définie comme suit :
Je suggère de diviser le travail en deux étapes : compter les recouvrements et compter les contacts.
Étant donné une séquence de déplacements, comment peut-on calculer le nombre de recouvrements ? Autrement dit, étant donné Move.Right, Move.Up, Move.Left, Move.Down, Move.Down, Move.Left, Move.Up, Move.Right, comment sait-on qu’il y a trois recouvrements ?
Le problème est lié à la représentation. La séquence de déplacements est utile pour les méthodes crossover et mutate, mais pas pour getFitness.
Une façon de résoudre ce problème est de créer une représentation temporaire lors du calcul de la valeur d’adaptation (fitness). Une représentation qui semble appropriée est celle présentée en classe.
Vous devriez être en mesure de traiter la séquence de déplacements Move.Right, Move.Up, Move.Left, Move.Down, Move.Down, Move.Left, Move.Up, Move.Right, afin de sauvegarder des informations utiles dans cette représentation temporaire. Quel est le type des éléments de cette représentation ? Quelle information est utile pour calculer le nombre de recouvrements ?
Lorsque vous aurez résolu ce problème, vous pouvez maintenant vous attaquer au problème du calcul du nombre de contacts. Un représentation similaire vous sera utile. Cette fois-ci compter le nombre de fois que l’on traverse une cellule ne sera pas suffisant. Quelle information serait utile pour déterminer le nombre de contacts ?
Non ! Vous devez soumettre un fichier .jar, tel qu’expliqué sur la page des consignes aux devoirs.
Vous ne devez pas ajouter des méthodes ou des variables publiques ; ce qui changerait l’interface de la classe. Vous pouvez cependant déclarer de nouvelles méthodes privées afin de faciliter la résolution de certains problèmes. En fait, je vous encourage fortement à le faire, dans le but d’améliorer la structure de vos programmes.
Avant Java 1.5, nous utilisions des constantes de type int afin de représenter des constantes symboliques, telles que les jours de la semaine ou les mois de l’année.
Cependant, comme le démontre l’exemple ci-haut, puisque toutes les constantes étaient représentées à l’aide d’entiers, le compilateur ne pouvait détecter les erreurs telles que l’affectation de la valeur d’une constante représentant un mois de l’année à une variable représentant un jour de la semaine.
Java 1.5 a introduit les types énumérés qui permettent le même type de constructions, mais de façon sécuritaire.
Si l’on ajoute la ligne qui suit à l’exemple ci-haut.
Le compilateur produira le message d’erreur qui suit.
Voici des informations complémentaires :
Non. Nous traiterons les cas d’erreurs lorsque nous aurons vu les exceptions.
Non ! Le générateur de nombres aléatoires (Math.random()) choisit au hasard une valeur parmi un ensemble fini de valeurs
prises dans l’intervalle 0.0 à 1.0. La taille de cet ensemble est N ; un très grand nombre puisque la valeur retournée est un
nombre en virgule flottante double précision. La probabilité que la valeur retournée soit x est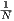 
; la valeur x, disons x = 0.8, est
l’une des N valeurs possible. Ainsi, la probabilité que la valeur retournée soit x est 
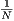, un bien petit nombre (près de
zéro).
Poursuivons l’explication. Math.random() choisit au hasard l’une des N valeurs possibles dans l’intervalle 0.0 à 1.0. Toutes ces
valeurs ont la même chance d’être choisies, 
. On dit aussi que la distribution est approximativement uniforme. Ainsi, si l’on fait
un très grand nombre d’appels à la méthode Math.random(), les valeurs retournées seront uniformément distribuées dans
l’intervalle 0.0 à 1.0. Certainement, 100% des valeurs seront plus petites ou égales à 1.0 ! Mais aussi, 95 % des valeurs seront
plus petites ou égales à 0.95, 90 % des valeurs seront plus petites ou égales à 0.90, etc. Voici un petit programme afin d’illustrer
tout ceci.
Premièrement, la description du devoir ne dit pas qu’il faut utiliser une méthode de tri, mon implémentation n’en utilise pas, ce que le devoir dit c’est que ≪ les individus de la population sont toujours en ordre croissant de valeur d’adaptation ≫.
Si vous deviez utiliser un algorithme de tri, ce qui mènerait à une implémentation plus lente, alors oui, vous pouvez utiliser la méthode de tri de l’API.
Oui, vous devez implémenter toutes les méthodes du devoir. La description du devoir est en quelque sorte une spécification et vous devez vous y conformer. Mais aussi, ces méthodes seront utilisées par nos programmes tests.
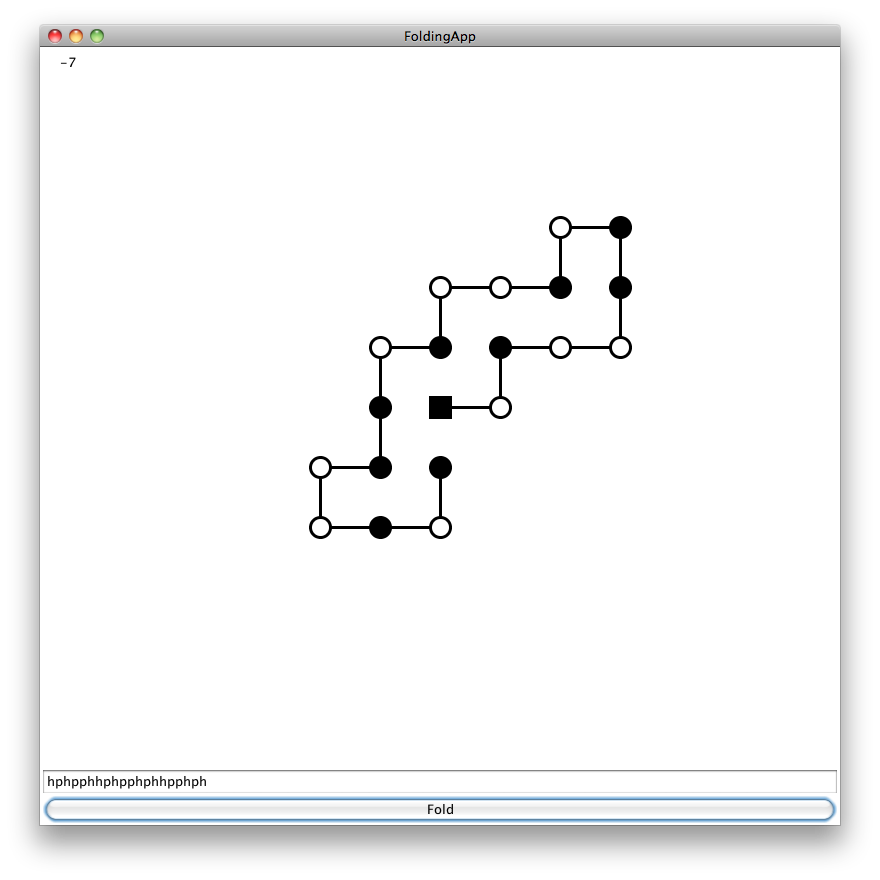
Afin de faciliter vos tests et le débogage de votre application, j’ai créé une interface usager qui vous permet d’entrer une chaîne et de visualiser le meilleur résultat trouvé par votre algorithme.
Modifié le : 1er février 2016