Introduction to Search

CSI 4106 - Fall 2024

Author

Marcel Turcotte

Published

Version: Nov 14, 2024 09:02

Preamble

Quote of the Day

;document.getElementById("tweet-19274").innerHTML = tweet["html"];

Learning Objectives

Understand the role of search algorithms in AI, crucial for planning, reasoning, and applications like AlphaGo.
Grasp key search concepts: state space, initial/goal states, actions, transition models, cost functions.
Learn differences and implementations of uninformed search algorithms (BFS and DFS).
Comprehend informed search strategies and heuristic functions’ role in search efficiency.
Implement and compare BFS, DFS, and Best-First Search using the 8-Puzzle problem.
Analyze performance and optimality of various search algorithms.

Today’s focus is primarily on providing justification, as well as introducing key concepts and terminology.

Justification

Silver et al. (2016)

Justification

We have honed our expertise in machine learning to a point where we possess a robust understanding of neural networks and deep learning, allowing us to develop simple models using Keras.

. . .

In recent years, Monte Carlo Tree Search (MCTS) has played a pivotal role in advancing artificial intelligence research. After initially concentrating on deep learning, we are now shifting our focus to search.

Justification

The integration of deep learning and MCTS underpins modern applications such as AlphaGo, AlphaZero, and MuZero.

. . .

Search algorithms are crucial in addressing challenges in planning and reasoning and are likely to become increasingly significant in future developments.

Search (a biased timeline)

1968 – A*: Heuristic-based search, foundational for pathfinding and planning in AI.
1970s-1980s – Population-Based Algorithms (e.g., Genetic Algorithms): Stochastic optimization approaches useful for large, complex search spaces.
1980s – Constraint Satisfaction Problems (CSPs): Search in structured spaces with explicit constraints; a precursor to formal problem-solving systems.
2013 – DQN: Reinforcement learning via search (Q-learning) from raw input (pixels).
2015 – AlphaGo: Game-tree search with Monte Carlo Tree Search (MCTS) combined with deep learning.
2017 – AlphaZero: Generalized self-play with MCTS in multiple domains.
2019 – MuZero: Search in unknown environments without predefined models.
2020 – Agent57: Generalized search across multiple environments (Atari games).
2020 – AlphaGeometry: Search-based theorem proving in mathematical spaces.
2021 – FunSearch: Potentially another generalization of search techniques.

Search

The computer that mastered Go. Nature Video posted on YouTube on 2016-01-27. (7m 52s)

In 1997, IBM’s Deep Blue defeated the reigning world chess champion, Garry Kasparov. However, the AI community was not particularly impressed, as the system’s primary accomplishment lay in its ability to evaluate 200 million chess positions per second. Following the match, Kasparov remarked that Deep Blue was “as intelligent as your alarm clock.”

Since then, significant advancements have been made. Unlike Deep Blue, AlphaZero relies on “more interesting approaches than brute-force search, which are perhaps more human-like in the way that they deal with the position.” This prompted Kasparov to express his approval, stating, “I can’t hide my satisfaction that [AlphaZero] plays with a dynamic style reminiscent of my own!”

AlphaGo - The Movie

Yes, AlphaGo successfully defeated the world champion, Lee Sedol. (1h 30m)

AlphaGo2MuZero

Attribution: MuZero: Mastering Go, chess, shogi and Atari without rules, Google DeepMind, 2020-12-23. Schrittwieser et al. (2020)

David Silver, a principal research scientist at DeepMind and a professor at University College London, is one of the leading researchers on these projects. He earned his PhD at the University of Alberta, where he was supervised by Richard Sutton.

You might also want to watch the following video: AlphaGo Zero: Discovering new knowledge. Posted on YouTube on 2017-10-18.

Search

Applications

Pathfinding and Navigation: Used in robotics and video games to find a path from a starting point to a destination.
Puzzle Solving: Solving puzzles like the 8-puzzle, mazes, or Sudoku.
Network Analysis: Analyzing networks and graphs, such as finding connectivity or shortest paths in social networks or transportation maps.
Game Playing: Used to evaluate moves in games like chess or Go, especially when combined with other strategies.

Applications

Scheduling: Planning and scheduling tasks in manufacturing, project management, or airline scheduling.
Resource Allocation: Allocating resources in a network or within an organization where constraints must be satisfied.
Configuration Problems: Solving problems where a set of components must be assembled to meet specific requirements, such as configuring a computer system or designing a circuit.

Applications

Decision Making under Uncertainty: Used in real-time strategy games and simulations where decisions need to be evaluated under uncertain conditions.
Storrytelling: LLMs can effectively generate stories when guided by a valid input plan from an automated planner. (Simon and Muise 2024)

The applications of search algorithms are both numerous and diverse.

Search has been an active area of research not only because of its wide range of applications but also due to the potential for improvements in algorithms to significantly reduce program execution time or facilitate the exploration of larger search spaces.

Outline

Deterministic & Heuristic Search: BFS, DFS, A* for pathfinding and optimization in classical AI.
CSPs & Population-Based Algorithms: Focus on structured problems and stochastic search.
Adversarial Game Algorithms: Minimax, alpha-beta pruning, MCTS for decision-making in competitive environments.

This lecture and the upcoming ones will thoroughly cover these topics.

Definition

(Russell and Norvig 2020, 63)

When the correct action to take is not immediately obvious, an agent may need to to plan ahead: to consider a sequence of actions that form a path to a goal state. Such an agent is called a problem-solving agent, and the computational process it undertakes is called search.

Terminology

An agent is an entity that performs actions. A rational agent is one that acts to achieve the “best” outcome. Conceptually, an agent perceives its environment through sensors and interacts with it using actuators.

The definition of an agent in artificial intelligence (AI) shares some similarities with the psychological definition, but there are key distinctions. In AI, an agent is an autonomous entity that perceives its environment through sensors and acts upon it using actuators to achieve specific goals. Both definitions involve perception, decision-making, and action.

However, while psychological agents are human or biological and involve complex cognitive and emotional processes, AI agents are computational and operate based on algorithms designed to maximize certain performance measures or achieve predefined objectives. The focus in AI is more on the technical implementation of these processes, whereas in psychology, the emphasis is on understanding the cognitive and motivational aspects of agency.

The concept of agentic design in software engineering and artificial intelligence has experienced a resurgence in popularity.

Environment Characteristics

Observability: Partially observable, or fully observable
Agent Composition: Single or multiple agents
Predictability: Deterministic or non-deterministic
State Dependency: Stateless or stateful
Temporal Dynamics: Static or dynamic
State Representation: Discrete or continuous

In this lecture, environments are assumed to be: fully observable, single agent, stateless, deterministic, static, and discrete.

The characteristics of an environment influence the complexity of problem-solving.

A fully observable environment allows the agent to detect all relevant aspects for decision-making.
In a deterministic environment, the agent can predict the next state based on the current state and its subsequent action.
Stateless (Episodic) Environments involve decisions or actions that are independent of prior actions, with experiences divided into unrelated episodes. An example is a classification problem.
Stateful (Sequential) Environments require that each action’s outcome can affect future decisions, as the sequence of actions impacts the state and subsequent choices. An example is a chess game.
A dynamic environment is characterized by changes in context while the agent is deliberating.
Chess serves as an example of a discrete environment, with a finite, though large, number of states. In contrast, an autonomous vehicle operates within a continuous-state and continuous-time environment.

Problem-Solving Process

Search: The process involves simulating sequences of actions until the agent achieves its goal. A successful sequence is termed a solution.

A precise formulation facilitates the development of reusable code.

An environment characterized as stateless, single-agent, fully observable, deterministic, static, and discrete implies that the solution to any problem within this context is a fixed sequence of actions.

Stateless: Each decision is independent of previous actions, meaning the solution does not depend on history.
Single Agent: There is no interaction with other agents that could introduce variability.
Fully Observable: The agent has complete information about the environment, allowing for precise decision-making.
Deterministic: The outcome of actions is predictable, with no randomness affecting the result.
Static: The environment does not change over time, so the conditions remain constant.
Discrete: The environment has a finite number of states and actions, enabling a clear sequence of steps.

I anticipate that you are already familiar with these concepts, and thus, this initial lecture primarily serves as a review.

Search Problem Definition

A collection of states, referred to as the state space.
An initial state where the agent begins.
One or more goal states that define successful outcomes.
A set of actions available in a given state \(s\).
A transition model that determines the next state based on the current state and selected action.
An action cost function that specifies the cost of performing action \(a\) in state \(s\) to reach state \(s'\).

Definitions

A path is defined as a sequence of actions.
A solution is a path that connects the initial state to the goal state.
An optimal solution is the path with the lowest cost among all possible solutions.

We assume that the path cost is the sum of the individual action costs, and all costs are positive. The state space can be conceptualized as a graph, where the nodes represent the states and the edges correspond to the actions.

In certain problems, multiple optimal solutions may exist. However, it is typically sufficient to identify and report a single optimal solution. Providing all optimal solutions can significantly increase time and space complexity for some problems.

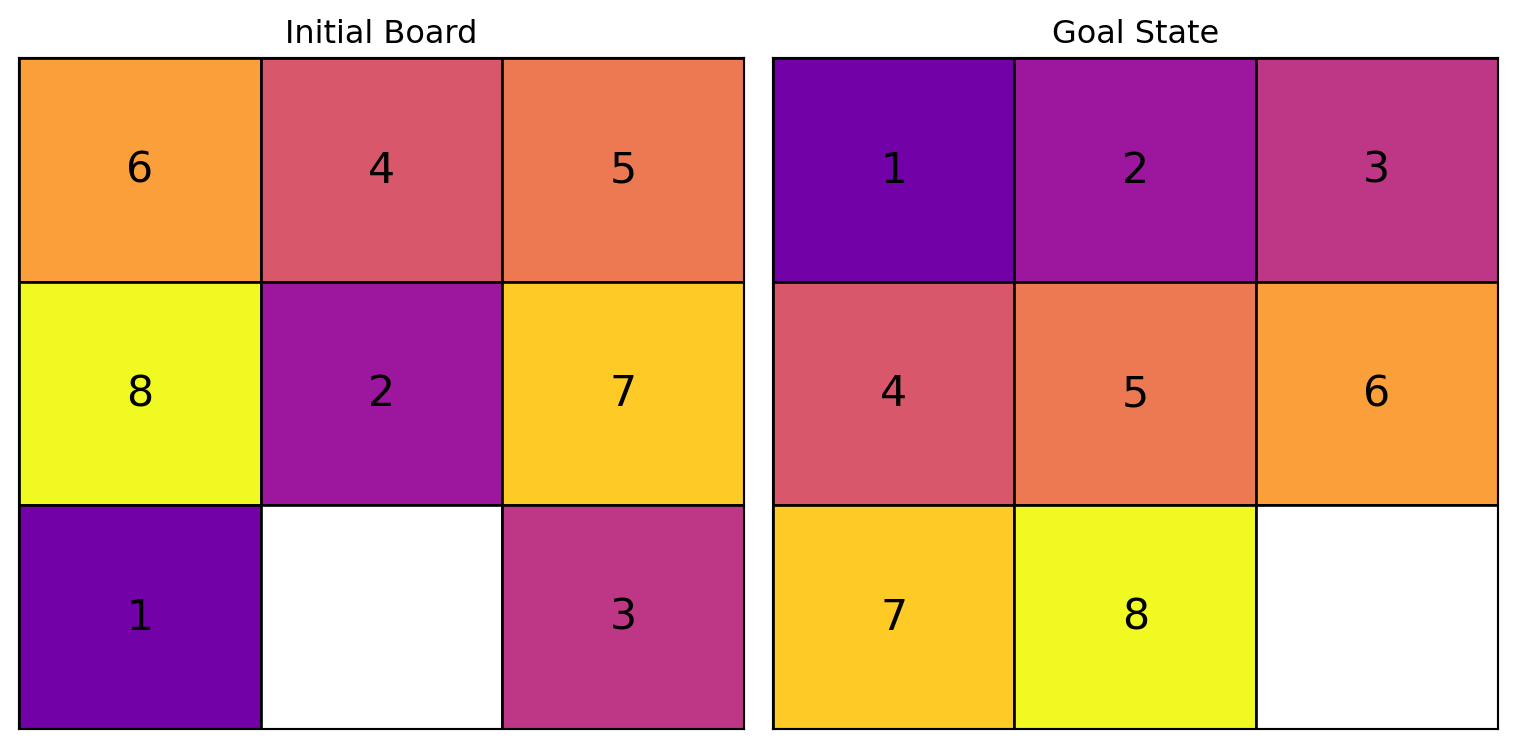
Example: 8-Puzzle

8-Puzzle

How can the states be represented?
What constitutes the initial state?
What defines the actions?
What would constitute a path?
What characterizes the goal state?
What would constitute a solution?
What should be the cost of an action?

Each state can be represented as a list containing the numbers 0 to 8. Each number corresponds to a tile, and its position in the list reflects its location in the grid, with 0 denoting the blank space.
The initial state is a permutation of the numbers 0 to 8.
Actions include left, right, up, and down, which involve sliding an adjacent tile into the blank space.
A path would be a sequence of actions, say left, left, up.
The transition model maps a given state and action to a new state. Not all actions are feasible from every state; for instance, if the blank space is at the edge of the grid, only certain moves are possible, such as down, up, or left.
The goal state is achieved when the list is ordered from 1 to 8, followed by 0, indicating that the tiles are arranged correctly. How many goal states are there?
A solution would be a valid path transforming an initial state into a goal state.
Each action incurs a cost of 1.

How many possible states are there?

There are 9! = 362,880 states. Brut force is feasible.

How many states are there for the 15-Puzzle?

15! = 1,307,674,368,000 (1.3 trillion)!

Search Tree

A search tree is a conceptual tree structure where nodes represent states in a state space, and edges represent possible actions, facilitating systematic exploration to find a path from an initial state to a goal state.

The search algorithms we examine today construct a search tree, where each node represents a state within the state space and each edge represents an action.

It is important to distinguish between the search tree and the state space, which can be depicted as a graph. The structure of the search tree varies depending on the algorithm employed to address the search problem.

Search Tree

An example of a search tree for the 8-Puzzle. The solution here is incomplete.

Search Tree

The root of the search tree represents the initial state of the problem.
Expanding a node involves evaluating all possible actions available from that state.
The result of an action is the new state achieved after applying that action to the current state.
Similar to other tree structures, each node (except for the root and leaf nodes) has a parent and may have children.

A distinctive feature of a search algorithm is its method for selecting the next node to expand.

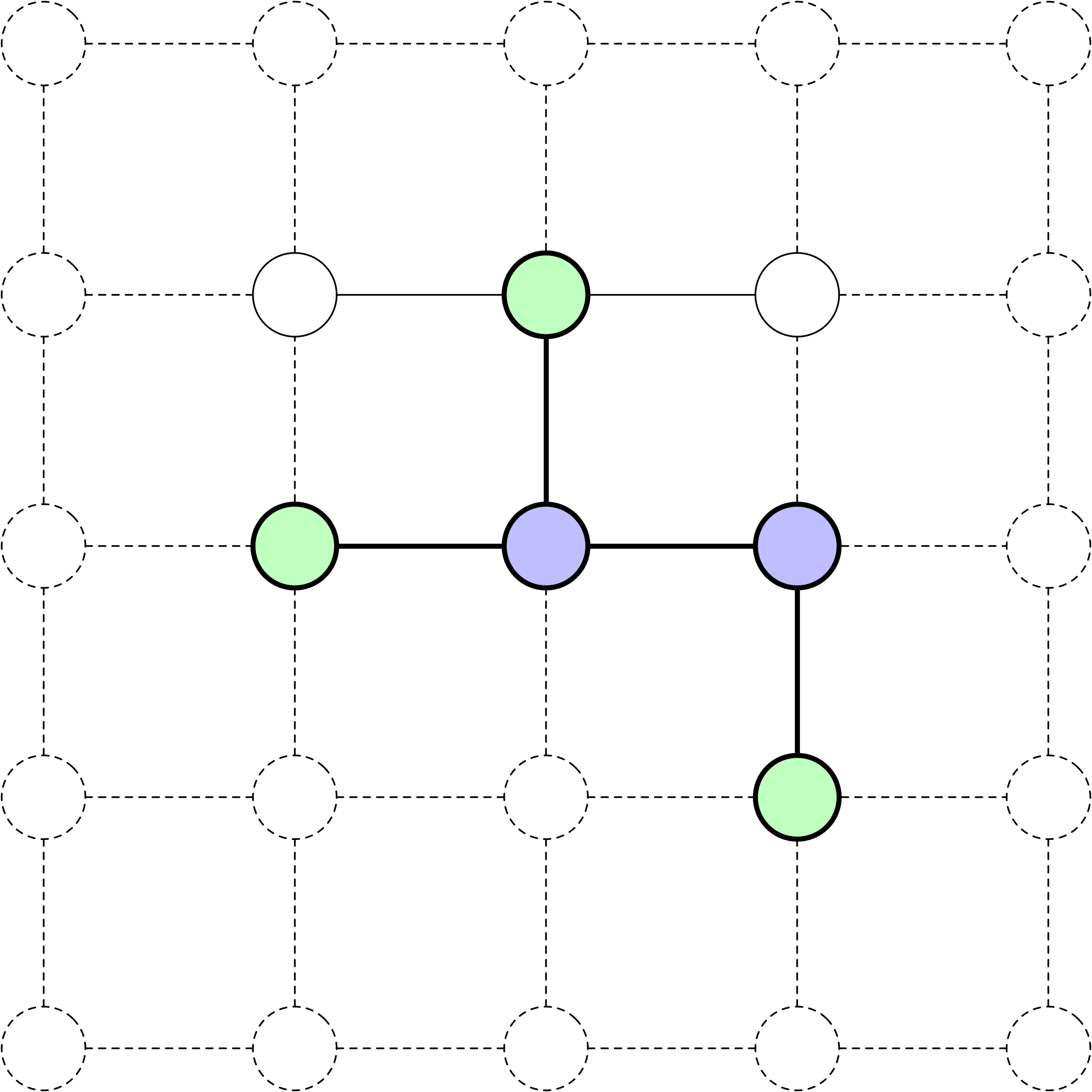
Frontier

Any state corresponding to a node in the search tree is considered reached. Frontier nodes are those that have been reached but have not yet been expanded. Above, there are 10 expanded nodes and 11 frontier nodes, resulting in a total of 21 nodes that have been reached.

Frontier

In the 8-Puzzle, four actions are possible: slide left, right, up, or down. The search can be visualized on a grid: purple nodes: expanded states, green nodes: frontier states (reached but not expanded).

The diagrams correspond to the search tree presented on the previous page. For example, the initial state can be expanded using three actions: slide left, right, and up. Node (2, 3) can only be expanded by sliding down, while node (3, 3) can be expanded by sliding left and down.

Frontier

Uninformed search

Definition

An uninformed search is a search strategy that explores the search space using only the information available in the problem definition, without any domain-specific knowledge, evaluating nodes based solely on their inherent properties rather than estimated costs or heuristics.

State Representation

initial_state_8 = [6, 4, 5,
                   8, 2, 7,
                   1, 0, 3]

goal_state_8 = [1, 2, 3,
                4, 5, 6,
                7, 8, 0]

The states are represented as lists of numbers. 0 represents the blank tile.

`is_goal`

def is_goal(state, goal_state):
    """Determines if a given state matches the goal state."""
    return state == goal_state

Auxilliary method.

`expand`

def expand(state):
    """Generates successor states by moving the blank tile in all possible directions."""
    size = int(len(state) ** 0.5)  # Determine puzzle size (3 for 8-puzzle, 4 for 15-puzzle)
    idx = state.index(0)  # Find the index of the blank tile represented by 0
    x, y = idx % size, idx // size  # Convert index to (x, y) coordinates
    neighbors = []

    # Define possible moves: Left, Right, Up, Down
    moves = [(-1, 0), (1, 0), (0, -1), (0, 1)]
    for dx, dy in moves:
        nx, ny = x + dx, y + dy
        # Check if the new position is within the puzzle boundaries
        if 0 <= nx < size and 0 <= ny < size:
            n_idx = ny * size + nx
            new_state = state.copy()
            # Swap the blank tile with the adjacent tile
            new_state[idx], new_state[n_idx] = new_state[n_idx], new_state[idx]
            neighbors.append(new_state)
    return neighbors

`expand`

expand(initial_state_8)

[[6, 4, 5, 8, 2, 7, 0, 1, 3],
 [6, 4, 5, 8, 2, 7, 1, 3, 0],
 [6, 4, 5, 8, 0, 7, 1, 2, 3]]

`is_empty`

def is_empty(frontier):
    """Checks if the frontier is empty."""
    return len(frontier) == 0

If the frontier becomes empty (no more nodes to be expanded), the problem has no solution.

Are there 8-Puzzle boards that have no solutions?

The solvability of the 8-puzzle depends on the number of inversions in the initial state. An inversion is a pair of tiles where a higher-numbered tile precedes a lower-numbered tile when the puzzle is viewed as a sequence (excluding the blank tile).

`print_solution`

def print_solution(solution):
    """Prints the sequence of steps from the initial to the goal state."""
    size = int(len(solution[0]) ** 0.5)
    for step, state in enumerate(solution):
        print(f"Step {step}:")
        for i in range(size):
            row = state[i*size:(i+1)*size]
            print(' '.join(str(n) if n != 0 else ' ' for n in row))
        print()

Cycles

A path that revisits the same states forms a cycle.

Allowing cycles would render the resulting search tree infinite.

To prevent this, we monitor the states that have been reached, though this incurs a memory cost.

Breadth-first search

from collections import deque

Breadth-first search (BFS) employs a queue to manage the frontier nodes, which are also known as the open list.

Breadth-first search

def bfs(initial_state, goal_state):

    frontier = deque()  # Initialize the queue for BFS
    frontier.append((initial_state, []))  # Each element is a tuple: (state, path)

    explored = set()
    explored.add(tuple(initial_state))

    iterations = 0 # simply used to compare algorithms

    while not is_empty(frontier):
        current_state, path = frontier.popleft()

        if is_goal(current_state, goal_state):
            print(f"Number of iterations: {iterations}")
            return path + [current_state]  # Return the successful path

        iterations = iterations + 1

        for neighbor in expand(current_state):
            neighbor_tuple = tuple(neighbor)
            if neighbor_tuple not in explored:
                explored.add(neighbor_tuple)
                frontier.append((neighbor, path + [current_state]))

    return None  # No solution found

Find the shortest path from the initial state to the goal state.

Simple Case

Number of iterations: 12

initial_state_8 = [1, 2, 3,
                    4, 0, 6,
                    7, 5, 8]
goal_state_8 = [1, 2, 3,
                4, 5, 6,
                7, 8, 0]

bfs(initial_state_8, goal_state_8)

Number of iterations: 12

[[1, 2, 3, 4, 0, 6, 7, 5, 8],
 [1, 2, 3, 4, 5, 6, 7, 0, 8],
 [1, 2, 3, 4, 5, 6, 7, 8, 0]]

Challenging Case

initial_state_8 = [6, 4, 5,
                   8, 2, 7,
                   1, 0, 3]
goal_state_8 = [1, 2, 3,
                4, 5, 6,
                7, 8, 0]

print("Solving 8-puzzle with BFS...")

solution_8_bfs = bfs(initial_state_8, goal_state_8)

if solution_8_bfs:
    print(f"BFS Solution found in {len(solution_8_bfs) - 1} moves:")
    print_solution(solution_8_bfs)
else:
    print("No solution found for 8-puzzle using BFS.")

Solving 8-puzzle with BFS...
Number of iterations: 145605
BFS Solution found in 25 moves:
Step 0:
6 4 5
8 2 7
1   3

Step 1:
6 4 5
8 2 7
  1 3

Step 2:
6 4 5
  2 7
8 1 3

Step 3:
6 4 5
2   7
8 1 3

Step 4:
6   5
2 4 7
8 1 3

Step 5:
  6 5
2 4 7
8 1 3

Step 6:
2 6 5
  4 7
8 1 3

Step 7:
2 6 5
4   7
8 1 3

Step 8:
2 6 5
4 1 7
8   3

Step 9:
2 6 5
4 1 7
  8 3

Step 10:
2 6 5
  1 7
4 8 3

Step 11:
2 6 5
1   7
4 8 3

Step 12:
2 6 5
1 7  
4 8 3

Step 13:
2 6 5
1 7 3
4 8  

Step 14:
2 6 5
1 7 3
4   8

Step 15:
2 6 5
1   3
4 7 8

Step 16:
2   5
1 6 3
4 7 8

Step 17:
2 5  
1 6 3
4 7 8

Step 18:
2 5 3
1 6  
4 7 8

Step 19:
2 5 3
1   6
4 7 8

Step 20:
2   3
1 5 6
4 7 8

Step 21:
  2 3
1 5 6
4 7 8

Step 22:
1 2 3
  5 6
4 7 8

Step 23:
1 2 3
4 5 6
  7 8

Step 24:
1 2 3
4 5 6
7   8

Step 25:
1 2 3
4 5 6
7 8

BFS Search Tree

The search tree above illustrates the first 20 iterations of the breadth-first search (BFS) for the specified initial goal.

Depth-First Search

def dfs(initial_state, goal_state):

    frontier = [(initial_state, [])]  # Each element is a tuple: (state, path)

    explored = set()
    explored.add(tuple(initial_state))

    iterations = 0

    while not is_empty(frontier):
        current_state, path = frontier.pop()

        if is_goal(current_state, goal_state):
            print(f"Number of iterations: {iterations}")
            return path + [current_state]  # Return the successful path

        iterations = iterations + 1

        for neighbor in expand(current_state):
            neighbor_tuple = tuple(neighbor)
            if neighbor_tuple not in explored:
                explored.add(neighbor_tuple)
                frontier.append((neighbor, path + [current_state]))

    return None  # No solution found

What is the behaviour of depth-First Search (dfs)?

Depth-First Search (DFS) consistently expands the deepest node.

When does the deepening process halt?

It ceases when all child nodes correspond to states that have already been visited.

What happens next?

The algorithm backtracks to the most recent frontier node.

If all children of this node also correspond to previously visited states, the algorithm continues to backtrack further.

DFS Search Tree

DFS Search Tree

Simple Case

Number of iterations: 2

initial_state_8 = [1, 2, 3,
                    4, 0, 6,
                    7, 5, 8]
goal_state_8 = [1, 2, 3,
                4, 5, 6,
                7, 8, 0]

bfs(initial_state_8, goal_state_8)

Number of iterations: 12

[[1, 2, 3, 4, 0, 6, 7, 5, 8],
 [1, 2, 3, 4, 5, 6, 7, 0, 8],
 [1, 2, 3, 4, 5, 6, 7, 8, 0]]

Challenging Case

initial_state_8 = [6, 4, 5,
                   8, 2, 7,
                   1, 0, 3]
goal_state_8 = [1, 2, 3,
                4, 5, 6,
                7, 8, 0]

print("Solving 8-puzzle with DFS...")

solution_8_bfs = dfs(initial_state_8, goal_state_8)

if solution_8_bfs:
    print(f"DFS Solution found in {len(solution_8_bfs) - 1} moves:")
    print_solution(solution_8_bfs)
else:
    print("No solution found for 8-puzzle using DFS.")

Solving 8-puzzle with DFS...
Number of iterations: 1187
DFS Solution found in 1157 moves:
Step 0:
6 4 5
8 2 7
1   3

Step 1:
6 4 5
8   7
1 2 3

Step 2:
6   5
8 4 7
1 2 3

Step 3:
6 5  
8 4 7
1 2 3

Step 4:
6 5 7
8 4  
1 2 3

Step 5:
6 5 7
8 4 3
1 2  

Step 6:
6 5 7
8 4 3
1   2

Step 7:
6 5 7
8   3
1 4 2

Step 8:
6   7
8 5 3
1 4 2

Step 9:
6 7  
8 5 3
1 4 2

Step 10:
6 7 3
8 5  
1 4 2

Step 11:
6 7 3
8 5 2
1 4  

Step 12:
6 7 3
8 5 2
1   4

Step 13:
6 7 3
8   2
1 5 4

Step 14:
6   3
8 7 2
1 5 4

Step 15:
6 3  
8 7 2
1 5 4

Step 16:
6 3 2
8 7  
1 5 4

Step 17:
6 3 2
8 7 4
1 5  

Step 18:
6 3 2
8 7 4
1   5

Step 19:
6 3 2
8   4
1 7 5

Step 20:
6   2
8 3 4
1 7 5

Step 21:
6 2  
8 3 4
1 7 5

Step 22:
6 2 4
8 3  
1 7 5

Step 23:
6 2 4
8 3 5
1 7  

Step 24:
6 2 4
8 3 5
1   7

Step 25:
6 2 4
8   5
1 3 7

Step 26:
6   4
8 2 5
1 3 7

Step 27:
6 4  
8 2 5
1 3 7

Step 28:
6 4 5
8 2  
1 3 7

Step 29:
6 4 5
8   2
1 3 7

Step 30:
6 4 5
8 3 2
1   7

Step 31:
6 4 5
8 3 2
1 7  

Step 32:
6 4 5
8 3  
1 7 2

Step 33:
6 4  
8 3 5
1 7 2

Step 34:
6   4
8 3 5
1 7 2

Step 35:
6 3 4
8   5
1 7 2

Step 36:
6 3 4
8 7 5
1   2

Step 37:
6 3 4
8 7 5
1 2  

Step 38:
6 3 4
8 7  
1 2 5

Step 39:
6 3  
8 7 4
1 2 5

Step 40:
6   3
8 7 4
1 2 5

Step 41:
6 7 3
8   4
1 2 5

Step 42:
6 7 3
8 2 4
1   5

Step 43:
6 7 3
8 2 4
  1 5

Step 44:
6 7 3
  2 4
8 1 5

Step 45:
  7 3
6 2 4
8 1 5

Step 46:
7   3
6 2 4
8 1 5

Step 47:
7 2 3
6   4
8 1 5

Step 48:
7 2 3
6 1 4
8   5

Step 49:
7 2 3
6 1 4
8 5  

Step 50:
7 2 3
6 1  
8 5 4

Step 51:
7 2  
6 1 3
8 5 4

Step 52:
7   2
6 1 3
8 5 4

Step 53:
7 1 2
6   3
8 5 4

Step 54:
7 1 2
6 5 3
8   4

Step 55:
7 1 2
6 5 3
8 4  

Step 56:
7 1 2
6 5  
8 4 3

Step 57:
7 1  
6 5 2
8 4 3

Step 58:
7   1
6 5 2
8 4 3

Step 59:
7 5 1
6   2
8 4 3

Step 60:
7 5 1
6 4 2
8   3

Step 61:
7 5 1
6 4 2
8 3  

Step 62:
7 5 1
6 4  
8 3 2

Step 63:
7 5  
6 4 1
8 3 2

Step 64:
7   5
6 4 1
8 3 2

Step 65:
7 4 5
6   1
8 3 2

Step 66:
7 4 5
6 3 1
8   2

Step 67:
7 4 5
6 3 1
8 2  

Step 68:
7 4 5
6 3  
8 2 1

Step 69:
7 4  
6 3 5
8 2 1

Step 70:
7   4
6 3 5
8 2 1

Step 71:
7 3 4
6   5
8 2 1

Step 72:
7 3 4
6 2 5
8   1

Step 73:
7 3 4
6 2 5
8 1  

Step 74:
7 3 4
6 2  
8 1 5

Step 75:
7 3 4
6   2
8 1 5

Step 76:
7 3 4
6 1 2
8   5

Step 77:
7 3 4
6 1 2
8 5  

Step 78:
7 3 4
6 1  
8 5 2

Step 79:
7 3  
6 1 4
8 5 2

Step 80:
7   3
6 1 4
8 5 2

Step 81:
7 1 3
6   4
8 5 2

Step 82:
7 1 3
6 5 4
8   2

Step 83:
7 1 3
6 5 4
8 2  

Step 84:
7 1 3
6 5  
8 2 4

Step 85:
7 1  
6 5 3
8 2 4

Step 86:
7   1
6 5 3
8 2 4

Step 87:
7 5 1
6   3
8 2 4

Step 88:
7 5 1
6 2 3
8   4

Step 89:
7 5 1
6 2 3
  8 4

Step 90:
7 5 1
  2 3
6 8 4

Step 91:
  5 1
7 2 3
6 8 4

Step 92:
5   1
7 2 3
6 8 4

Step 93:
5 2 1
7   3
6 8 4

Step 94:
5 2 1
7 8 3
6   4

Step 95:
5 2 1
7 8 3
6 4  

Step 96:
5 2 1
7 8  
6 4 3

Step 97:
5 2  
7 8 1
6 4 3

Step 98:
5   2
7 8 1
6 4 3

Step 99:
5 8 2
7   1
6 4 3

Step 100:
5 8 2
7 4 1
6   3

Step 101:
5 8 2
7 4 1
6 3  

Step 102:
5 8 2
7 4  
6 3 1

Step 103:
5 8  
7 4 2
6 3 1

Step 104:
5   8
7 4 2
6 3 1

Step 105:
5 4 8
7   2
6 3 1

Step 106:
5 4 8
7 3 2
6   1

Step 107:
5 4 8
7 3 2
6 1  

Step 108:
5 4 8
7 3  
6 1 2

Step 109:
5 4  
7 3 8
6 1 2

Step 110:
5   4
7 3 8
6 1 2

Step 111:
5 3 4
7   8
6 1 2

Step 112:
5 3 4
7 1 8
6   2

Step 113:
5 3 4
7 1 8
6 2  

Step 114:
5 3 4
7 1  
6 2 8

Step 115:
5 3  
7 1 4
6 2 8

Step 116:
5   3
7 1 4
6 2 8

Step 117:
5 1 3
7   4
6 2 8

Step 118:
5 1 3
7 2 4
6   8

Step 119:
5 1 3
7 2 4
6 8  

Step 120:
5 1 3
7 2  
6 8 4

Step 121:
5 1 3
7   2
6 8 4

Step 122:
5 1 3
7 8 2
6   4

Step 123:
5 1 3
7 8 2
6 4  

Step 124:
5 1 3
7 8  
6 4 2

Step 125:
5 1  
7 8 3
6 4 2

Step 126:
5   1
7 8 3
6 4 2

Step 127:
5 8 1
7   3
6 4 2

Step 128:
5 8 1
7 4 3
6   2

Step 129:
5 8 1
7 4 3
6 2  

Step 130:
5 8 1
7 4  
6 2 3

Step 131:
5 8  
7 4 1
6 2 3

Step 132:
5   8
7 4 1
6 2 3

Step 133:
5 4 8
7   1
6 2 3

Step 134:
5 4 8
7 2 1
6   3

Step 135:
5 4 8
7 2 1
  6 3

Step 136:
5 4 8
  2 1
7 6 3

Step 137:
  4 8
5 2 1
7 6 3

Step 138:
4   8
5 2 1
7 6 3

Step 139:
4 2 8
5   1
7 6 3

Step 140:
4 2 8
5 6 1
7   3

Step 141:
4 2 8
5 6 1
7 3  

Step 142:
4 2 8
5 6  
7 3 1

Step 143:
4 2  
5 6 8
7 3 1

Step 144:
4   2
5 6 8
7 3 1

Step 145:
4 6 2
5   8
7 3 1

Step 146:
4 6 2
5 3 8
7   1

Step 147:
4 6 2
5 3 8
7 1  

Step 148:
4 6 2
5 3  
7 1 8

Step 149:
4 6  
5 3 2
7 1 8

Step 150:
4   6
5 3 2
7 1 8

Step 151:
4 3 6
5   2
7 1 8

Step 152:
4 3 6
5 1 2
7   8

Step 153:
4 3 6
5 1 2
7 8  

Step 154:
4 3 6
5 1  
7 8 2

Step 155:
4 3  
5 1 6
7 8 2

Step 156:
4   3
5 1 6
7 8 2

Step 157:
4 1 3
5   6
7 8 2

Step 158:
4 1 3
5 8 6
7   2

Step 159:
4 1 3
5 8 6
7 2  

Step 160:
4 1 3
5 8  
7 2 6

Step 161:
4 1  
5 8 3
7 2 6

Step 162:
4   1
5 8 3
7 2 6

Step 163:
4 8 1
5   3
7 2 6

Step 164:
4 8 1
5 2 3
7   6

Step 165:
4 8 1
5 2 3
7 6  

Step 166:
4 8 1
5 2  
7 6 3

Step 167:
4 8 1
5   2
7 6 3

Step 168:
4 8 1
5 6 2
7   3

Step 169:
4 8 1
5 6 2
7 3  

Step 170:
4 8 1
5 6  
7 3 2

Step 171:
4 8  
5 6 1
7 3 2

Step 172:
4   8
5 6 1
7 3 2

Step 173:
4 6 8
5   1
7 3 2

Step 174:
4 6 8
5 3 1
7   2

Step 175:
4 6 8
5 3 1
7 2  

Step 176:
4 6 8
5 3  
7 2 1

Step 177:
4 6  
5 3 8
7 2 1

Step 178:
4   6
5 3 8
7 2 1

Step 179:
4 3 6
5   8
7 2 1

Step 180:
4 3 6
5 2 8
7   1

Step 181:
4 3 6
5 2 8
  7 1

Step 182:
4 3 6
  2 8
5 7 1

Step 183:
  3 6
4 2 8
5 7 1

Step 184:
3   6
4 2 8
5 7 1

Step 185:
3 2 6
4   8
5 7 1

Step 186:
3 2 6
4 7 8
5   1

Step 187:
3 2 6
4 7 8
5 1  

Step 188:
3 2 6
4 7  
5 1 8

Step 189:
3 2  
4 7 6
5 1 8

Step 190:
3   2
4 7 6
5 1 8

Step 191:
3 7 2
4   6
5 1 8

Step 192:
3 7 2
4 1 6
5   8

Step 193:
3 7 2
4 1 6
5 8  

Step 194:
3 7 2
4 1  
5 8 6

Step 195:
3 7  
4 1 2
5 8 6

Step 196:
3   7
4 1 2
5 8 6

Step 197:
3 1 7
4   2
5 8 6

Step 198:
3 1 7
4 8 2
5   6

Step 199:
3 1 7
4 8 2
5 6  

Step 200:
3 1 7
4 8  
5 6 2

Step 201:
3 1  
4 8 7
5 6 2

Step 202:
3   1
4 8 7
5 6 2

Step 203:
3 8 1
4   7
5 6 2

Step 204:
3 8 1
4 6 7
5   2

Step 205:
3 8 1
4 6 7
5 2  

Step 206:
3 8 1
4 6  
5 2 7

Step 207:
3 8  
4 6 1
5 2 7

Step 208:
3   8
4 6 1
5 2 7

Step 209:
3 6 8
4   1
5 2 7

Step 210:
3 6 8
4 2 1
5   7

Step 211:
3 6 8
4 2 1
5 7  

Step 212:
3 6 8
4 2  
5 7 1

Step 213:
3 6 8
4   2
5 7 1

Step 214:
3 6 8
4 7 2
5   1

Step 215:
3 6 8
4 7 2
5 1  

Step 216:
3 6 8
4 7  
5 1 2

Step 217:
3 6  
4 7 8
5 1 2

Step 218:
3   6
4 7 8
5 1 2

Step 219:
3 7 6
4   8
5 1 2

Step 220:
3 7 6
4 1 8
5   2

Step 221:
3 7 6
4 1 8
5 2  

Step 222:
3 7 6
4 1  
5 2 8

Step 223:
3 7  
4 1 6
5 2 8

Step 224:
3   7
4 1 6
5 2 8

Step 225:
3 1 7
4   6
5 2 8

Step 226:
3 1 7
4 2 6
5   8

Step 227:
3 1 7
4 2 6
  5 8

Step 228:
3 1 7
  2 6
4 5 8

Step 229:
  1 7
3 2 6
4 5 8

Step 230:
1   7
3 2 6
4 5 8

Step 231:
1 2 7
3   6
4 5 8

Step 232:
1 2 7
3 5 6
4   8

Step 233:
1 2 7
3 5 6
4 8  

Step 234:
1 2 7
3 5  
4 8 6

Step 235:
1 2  
3 5 7
4 8 6

Step 236:
1   2
3 5 7
4 8 6

Step 237:
1 5 2
3   7
4 8 6

Step 238:
1 5 2
3 8 7
4   6

Step 239:
1 5 2
3 8 7
4 6  

Step 240:
1 5 2
3 8  
4 6 7

Step 241:
1 5  
3 8 2
4 6 7

Step 242:
1   5
3 8 2
4 6 7

Step 243:
1 8 5
3   2
4 6 7

Step 244:
1 8 5
3 6 2
4   7

Step 245:
1 8 5
3 6 2
4 7  

Step 246:
1 8 5
3 6  
4 7 2

Step 247:
1 8  
3 6 5
4 7 2

Step 248:
1   8
3 6 5
4 7 2

Step 249:
1 6 8
3   5
4 7 2

Step 250:
1 6 8
3 7 5
4   2

Step 251:
1 6 8
3 7 5
4 2  

Step 252:
1 6 8
3 7  
4 2 5

Step 253:
1 6  
3 7 8
4 2 5

Step 254:
1   6
3 7 8
4 2 5

Step 255:
1 7 6
3   8
4 2 5

Step 256:
1 7 6
3 2 8
4   5

Step 257:
1 7 6
3 2 8
4 5  

Step 258:
1 7 6
3 2  
4 5 8

Step 259:
1 7 6
3   2
4 5 8

Step 260:
1 7 6
3 5 2
4   8

Step 261:
1 7 6
3 5 2
4 8  

Step 262:
1 7 6
3 5  
4 8 2

Step 263:
1 7  
3 5 6
4 8 2

Step 264:
1   7
3 5 6
4 8 2

Step 265:
1 5 7
3   6
4 8 2

Step 266:
1 5 7
3 8 6
4   2

Step 267:
1 5 7
3 8 6
4 2  

Step 268:
1 5 7
3 8  
4 2 6

Step 269:
1 5  
3 8 7
4 2 6

Step 270:
1   5
3 8 7
4 2 6

Step 271:
1 8 5
3   7
4 2 6

Step 272:
1 8 5
3 2 7
4   6

Step 273:
1 8 5
3 2 7
  4 6

Step 274:
1 8 5
  2 7
3 4 6

Step 275:
  8 5
1 2 7
3 4 6

Step 276:
8   5
1 2 7
3 4 6

Step 277:
8 2 5
1   7
3 4 6

Step 278:
8 2 5
1 4 7
3   6

Step 279:
8 2 5
1 4 7
3 6  

Step 280:
8 2 5
1 4  
3 6 7

Step 281:
8 2  
1 4 5
3 6 7

Step 282:
8   2
1 4 5
3 6 7

Step 283:
8 4 2
1   5
3 6 7

Step 284:
8 4 2
1 6 5
3   7

Step 285:
8 4 2
1 6 5
3 7  

Step 286:
8 4 2
1 6  
3 7 5

Step 287:
8 4  
1 6 2
3 7 5

Step 288:
8   4
1 6 2
3 7 5

Step 289:
8 6 4
1   2
3 7 5

Step 290:
8 6 4
1 7 2
3   5

Step 291:
8 6 4
1 7 2
3 5  

Step 292:
8 6 4
1 7  
3 5 2

Step 293:
8 6  
1 7 4
3 5 2

Step 294:
8   6
1 7 4
3 5 2

Step 295:
8 7 6
1   4
3 5 2

Step 296:
8 7 6
1 5 4
3   2

Step 297:
8 7 6
1 5 4
3 2  

Step 298:
8 7 6
1 5  
3 2 4

Step 299:
8 7  
1 5 6
3 2 4

Step 300:
8   7
1 5 6
3 2 4

Step 301:
8 5 7
1   6
3 2 4

Step 302:
8 5 7
1 2 6
3   4

Step 303:
8 5 7
1 2 6
3 4  

Step 304:
8 5 7
1 2  
3 4 6

Step 305:
8 5 7
1   2
3 4 6

Step 306:
8 5 7
1 4 2
3   6

Step 307:
8 5 7
1 4 2
3 6  

Step 308:
8 5 7
1 4  
3 6 2

Step 309:
8 5  
1 4 7
3 6 2

Step 310:
8   5
1 4 7
3 6 2

Step 311:
8 4 5
1   7
3 6 2

Step 312:
8 4 5
1 6 7
3   2

Step 313:
8 4 5
1 6 7
3 2  

Step 314:
8 4 5
1 6  
3 2 7

Step 315:
8 4  
1 6 5
3 2 7

Step 316:
8   4
1 6 5
3 2 7

Step 317:
8 6 4
1   5
3 2 7

Step 318:
8 6 4
1 2 5
3   7

Step 319:
8 6 4
1 2 5
  3 7

Step 320:
8 6 4
  2 5
1 3 7

Step 321:
8 6 4
2   5
1 3 7

Step 322:
8 6 4
2 3 5
1   7

Step 323:
8 6 4
2 3 5
1 7  

Step 324:
8 6 4
2 3  
1 7 5

Step 325:
8 6  
2 3 4
1 7 5

Step 326:
8   6
2 3 4
1 7 5

Step 327:
8 3 6
2   4
1 7 5

Step 328:
8 3 6
2 7 4
1   5

Step 329:
8 3 6
2 7 4
1 5  

Step 330:
8 3 6
2 7  
1 5 4

Step 331:
8 3  
2 7 6
1 5 4

Step 332:
8   3
2 7 6
1 5 4

Step 333:
8 7 3
2   6
1 5 4

Step 334:
8 7 3
2 5 6
1   4

Step 335:
8 7 3
2 5 6
1 4  

Step 336:
8 7 3
2 5  
1 4 6

Step 337:
8 7  
2 5 3
1 4 6

Step 338:
8   7
2 5 3
1 4 6

Step 339:
8 5 7
2   3
1 4 6

Step 340:
8 5 7
2 4 3
1   6

Step 341:
8 5 7
2 4 3
1 6  

Step 342:
8 5 7
2 4  
1 6 3

Step 343:
8 5  
2 4 7
1 6 3

Step 344:
8   5
2 4 7
1 6 3

Step 345:
8 4 5
2   7
1 6 3

Step 346:
8 4 5
2 6 7
1   3

Step 347:
8 4 5
2 6 7
1 3  

Step 348:
8 4 5
2 6  
1 3 7

Step 349:
8 4 5
2   6
1 3 7

Step 350:
8 4 5
2 3 6
1   7

Step 351:
8 4 5
2 3 6
1 7  

Step 352:
8 4 5
2 3  
1 7 6

Step 353:
8 4  
2 3 5
1 7 6

Step 354:
8   4
2 3 5
1 7 6

Step 355:
8 3 4
2   5
1 7 6

Step 356:
8 3 4
2 7 5
1   6

Step 357:
8 3 4
2 7 5
1 6  

Step 358:
8 3 4
2 7  
1 6 5

Step 359:
8 3  
2 7 4
1 6 5

Step 360:
8   3
2 7 4
1 6 5

Step 361:
8 7 3
2   4
1 6 5

Step 362:
8 7 3
2 6 4
1   5

Step 363:
8 7 3
2 6 4
  1 5

Step 364:
8 7 3
  6 4
2 1 5

Step 365:
  7 3
8 6 4
2 1 5

Step 366:
7   3
8 6 4
2 1 5

Step 367:
7 6 3
8   4
2 1 5

Step 368:
7 6 3
8 1 4
2   5

Step 369:
7 6 3
8 1 4
2 5  

Step 370:
7 6 3
8 1  
2 5 4

Step 371:
7 6  
8 1 3
2 5 4

Step 372:
7   6
8 1 3
2 5 4

Step 373:
7 1 6
8   3
2 5 4

Step 374:
7 1 6
8 5 3
2   4

Step 375:
7 1 6
8 5 3
2 4  

Step 376:
7 1 6
8 5  
2 4 3

Step 377:
7 1  
8 5 6
2 4 3

Step 378:
7   1
8 5 6
2 4 3

Step 379:
7 5 1
8   6
2 4 3

Step 380:
7 5 1
8 4 6
2   3

Step 381:
7 5 1
8 4 6
2 3  

Step 382:
7 5 1
8 4  
2 3 6

Step 383:
7 5  
8 4 1
2 3 6

Step 384:
7   5
8 4 1
2 3 6

Step 385:
7 4 5
8   1
2 3 6

Step 386:
7 4 5
8 3 1
2   6

Step 387:
7 4 5
8 3 1
2 6  

Step 388:
7 4 5
8 3  
2 6 1

Step 389:
7 4  
8 3 5
2 6 1

Step 390:
7   4
8 3 5
2 6 1

Step 391:
7 3 4
8   5
2 6 1

Step 392:
7 3 4
8 6 5
2   1

Step 393:
7 3 4
8 6 5
2 1  

Step 394:
7 3 4
8 6  
2 1 5

Step 395:
7 3 4
8   6
2 1 5

Step 396:
7 3 4
8 1 6
2   5

Step 397:
7 3 4
8 1 6
2 5  

Step 398:
7 3 4
8 1  
2 5 6

Step 399:
7 3  
8 1 4
2 5 6

Step 400:
7   3
8 1 4
2 5 6

Step 401:
7 1 3
8   4
2 5 6

Step 402:
7 1 3
8 5 4
2   6

Step 403:
7 1 3
8 5 4
2 6  

Step 404:
7 1 3
8 5  
2 6 4

Step 405:
7 1  
8 5 3
2 6 4

Step 406:
7   1
8 5 3
2 6 4

Step 407:
7 5 1
8   3
2 6 4

Step 408:
7 5 1
8 3  
2 6 4

Step 409:
7 5 1
8 3 4
2 6  

Step 410:
7 5 1
8 3 4
2   6

Step 411:
7 5 1
8 3 4
  2 6

Step 412:
7 5 1
  3 4
8 2 6

Step 413:
  5 1
7 3 4
8 2 6

Step 414:
5   1
7 3 4
8 2 6

Step 415:
5 3 1
7   4
8 2 6

Step 416:
5 3 1
7 2 4
8   6

Step 417:
5 3 1
7 2 4
8 6  

Step 418:
5 3 1
7 2  
8 6 4

Step 419:
5 3  
7 2 1
8 6 4

Step 420:
5   3
7 2 1
8 6 4

Step 421:
5 2 3
7   1
8 6 4

Step 422:
5 2 3
7 6 1
8   4

Step 423:
5 2 3
7 6 1
8 4  

Step 424:
5 2 3
7 6  
8 4 1

Step 425:
5 2  
7 6 3
8 4 1

Step 426:
5   2
7 6 3
8 4 1

Step 427:
5 6 2
7   3
8 4 1

Step 428:
5 6 2
7 4 3
8   1

Step 429:
5 6 2
7 4 3
8 1  

Step 430:
5 6 2
7 4  
8 1 3

Step 431:
5 6  
7 4 2
8 1 3

Step 432:
5   6
7 4 2
8 1 3

Step 433:
5 4 6
7   2
8 1 3

Step 434:
5 4 6
7 1 2
8   3

Step 435:
5 4 6
7 1 2
8 3  

Step 436:
5 4 6
7 1  
8 3 2

Step 437:
5 4  
7 1 6
8 3 2

Step 438:
5   4
7 1 6
8 3 2

Step 439:
5 1 4
7   6
8 3 2

Step 440:
5 1 4
7 3 6
8   2

Step 441:
5 1 4
7 3 6
8 2  

Step 442:
5 1 4
7 3  
8 2 6

Step 443:
5 1 4
7   3
8 2 6

Step 444:
5 1 4
7 2 3
8   6

Step 445:
5 1 4
7 2 3
8 6  

Step 446:
5 1 4
7 2  
8 6 3

Step 447:
5 1  
7 2 4
8 6 3

Step 448:
5   1
7 2 4
8 6 3

Step 449:
5 2 1
7   4
8 6 3

Step 450:
5 2 1
7 6 4
8   3

Step 451:
5 2 1
7 6 4
8 3  

Step 452:
5 2 1
7 6  
8 3 4

Step 453:
5 2  
7 6 1
8 3 4

Step 454:
5   2
7 6 1
8 3 4

Step 455:
5 6 2
7   1
8 3 4

Step 456:
5 6 2
7 3 1
8   4

Step 457:
5 6 2
7 3 1
  8 4

Step 458:
5 6 2
  3 1
7 8 4

Step 459:
  6 2
5 3 1
7 8 4

Step 460:
6   2
5 3 1
7 8 4

Step 461:
6 3 2
5   1
7 8 4

Step 462:
6 3 2
5 8 1
7   4

Step 463:
6 3 2
5 8 1
7 4  

Step 464:
6 3 2
5 8  
7 4 1

Step 465:
6 3  
5 8 2
7 4 1

Step 466:
6   3
5 8 2
7 4 1

Step 467:
6 8 3
5   2
7 4 1

Step 468:
6 8 3
5 4 2
7   1

Step 469:
6 8 3
5 4 2
7 1  

Step 470:
6 8 3
5 4  
7 1 2

Step 471:
6 8  
5 4 3
7 1 2

Step 472:
6   8
5 4 3
7 1 2

Step 473:
6 4 8
5   3
7 1 2

Step 474:
6 4 8
5 1 3
7   2

Step 475:
6 4 8
5 1 3
7 2  

Step 476:
6 4 8
5 1  
7 2 3

Step 477:
6 4  
5 1 8
7 2 3

Step 478:
6   4
5 1 8
7 2 3

Step 479:
6 1 4
5   8
7 2 3

Step 480:
6 1 4
5 2 8
7   3

Step 481:
6 1 4
5 2 8
7 3  

Step 482:
6 1 4
5 2  
7 3 8

Step 483:
6 1  
5 2 4
7 3 8

Step 484:
6   1
5 2 4
7 3 8

Step 485:
6 2 1
5   4
7 3 8

Step 486:
6 2 1
5 3 4
7   8

Step 487:
6 2 1
5 3 4
7 8  

Step 488:
6 2 1
5 3  
7 8 4

Step 489:
6 2 1
5   3
7 8 4

Step 490:
6 2 1
5 8 3
7   4

Step 491:
6 2 1
5 8 3
7 4  

Step 492:
6 2 1
5 8  
7 4 3

Step 493:
6 2  
5 8 1
7 4 3

Step 494:
6   2
5 8 1
7 4 3

Step 495:
6 8 2
5   1
7 4 3

Step 496:
6 8 2
5 4 1
7   3

Step 497:
6 8 2
5 4 1
7 3  

Step 498:
6 8 2
5 4  
7 3 1

Step 499:
6 8  
5 4 2
7 3 1

Step 500:
6   8
5 4 2
7 3 1

Step 501:
6 4 8
5   2
7 3 1

Step 502:
6 4 8
5 3 2
7   1

Step 503:
6 4 8
5 3 2
  7 1

Step 504:
6 4 8
  3 2
5 7 1

Step 505:
  4 8
6 3 2
5 7 1

Step 506:
4   8
6 3 2
5 7 1

Step 507:
4 3 8
6   2
5 7 1

Step 508:
4 3 8
6 7 2
5   1

Step 509:
4 3 8
6 7 2
5 1  

Step 510:
4 3 8
6 7  
5 1 2

Step 511:
4 3  
6 7 8
5 1 2

Step 512:
4   3
6 7 8
5 1 2

Step 513:
4 7 3
6   8
5 1 2

Step 514:
4 7 3
6 1 8
5   2

Step 515:
4 7 3
6 1 8
5 2  

Step 516:
4 7 3
6 1  
5 2 8

Step 517:
4 7  
6 1 3
5 2 8

Step 518:
4   7
6 1 3
5 2 8

Step 519:
4 1 7
6   3
5 2 8

Step 520:
4 1 7
6 2 3
5   8

Step 521:
4 1 7
6 2 3
5 8  

Step 522:
4 1 7
6 2  
5 8 3

Step 523:
4 1  
6 2 7
5 8 3

Step 524:
4   1
6 2 7
5 8 3

Step 525:
4 2 1
6   7
5 8 3

Step 526:
4 2 1
6 8 7
5   3

Step 527:
4 2 1
6 8 7
5 3  

Step 528:
4 2 1
6 8  
5 3 7

Step 529:
4 2  
6 8 1
5 3 7

Step 530:
4   2
6 8 1
5 3 7

Step 531:
4 8 2
6   1
5 3 7

Step 532:
4 8 2
6 3 1
5   7

Step 533:
4 8 2
6 3 1
5 7  

Step 534:
4 8 2
6 3  
5 7 1

Step 535:
4 8 2
6   3
5 7 1

Step 536:
4 8 2
6 7 3
5   1

Step 537:
4 8 2
6 7 3
5 1  

Step 538:
4 8 2
6 7  
5 1 3

Step 539:
4 8  
6 7 2
5 1 3

Step 540:
4   8
6 7 2
5 1 3

Step 541:
4 7 8
6   2
5 1 3

Step 542:
4 7 8
6 1 2
5   3

Step 543:
4 7 8
6 1 2
5 3  

Step 544:
4 7 8
6 1  
5 3 2

Step 545:
4 7  
6 1 8
5 3 2

Step 546:
4   7
6 1 8
5 3 2

Step 547:
4 1 7
6   8
5 3 2

Step 548:
4 1 7
6 3 8
5   2

Step 549:
4 1 7
6 3 8
  5 2

Step 550:
4 1 7
  3 8
6 5 2

Step 551:
  1 7
4 3 8
6 5 2

Step 552:
1   7
4 3 8
6 5 2

Step 553:
1 3 7
4   8
6 5 2

Step 554:
1 3 7
4 5 8
6   2

Step 555:
1 3 7
4 5 8
6 2  

Step 556:
1 3 7
4 5  
6 2 8

Step 557:
1 3  
4 5 7
6 2 8

Step 558:
1   3
4 5 7
6 2 8

Step 559:
1 5 3
4   7
6 2 8

Step 560:
1 5 3
4 2 7
6   8

Step 561:
1 5 3
4 2 7
6 8  

Step 562:
1 5 3
4 2  
6 8 7

Step 563:
1 5  
4 2 3
6 8 7

Step 564:
1   5
4 2 3
6 8 7

Step 565:
1 2 5
4   3
6 8 7

Step 566:
1 2 5
4 8 3
6   7

Step 567:
1 2 5
4 8 3
6 7  

Step 568:
1 2 5
4 8  
6 7 3

Step 569:
1 2  
4 8 5
6 7 3

Step 570:
1   2
4 8 5
6 7 3

Step 571:
1 8 2
4   5
6 7 3

Step 572:
1 8 2
4 7 5
6   3

Step 573:
1 8 2
4 7 5
6 3  

Step 574:
1 8 2
4 7  
6 3 5

Step 575:
1 8  
4 7 2
6 3 5

Step 576:
1   8
4 7 2
6 3 5

Step 577:
1 7 8
4   2
6 3 5

Step 578:
1 7 8
4 3 2
6   5

Step 579:
1 7 8
4 3 2
6 5  

Step 580:
1 7 8
4 3  
6 5 2

Step 581:
1 7 8
4   3
6 5 2

Step 582:
1 7 8
4 5 3
6   2

Step 583:
1 7 8
4 5 3
6 2  

Step 584:
1 7 8
4 5  
6 2 3

Step 585:
1 7  
4 5 8
6 2 3

Step 586:
1   7
4 5 8
6 2 3

Step 587:
1 5 7
4   8
6 2 3

Step 588:
1 5 7
4 2 8
6   3

Step 589:
1 5 7
4 2 8
6 3  

Step 590:
1 5 7
4 2  
6 3 8

Step 591:
1 5  
4 2 7
6 3 8

Step 592:
1   5
4 2 7
6 3 8

Step 593:
1 2 5
4   7
6 3 8

Step 594:
1 2 5
4 3 7
6   8

Step 595:
1 2 5
4 3 7
  6 8

Step 596:
1 2 5
  3 7
4 6 8

Step 597:
  2 5
1 3 7
4 6 8

Step 598:
2   5
1 3 7
4 6 8

Step 599:
2 3 5
1   7
4 6 8

Step 600:
2 3 5
1 6 7
4   8

Step 601:
2 3 5
1 6 7
4 8  

Step 602:
2 3 5
1 6  
4 8 7

Step 603:
2 3  
1 6 5
4 8 7

Step 604:
2   3
1 6 5
4 8 7

Step 605:
2 6 3
1   5
4 8 7

Step 606:
2 6 3
1 8 5
4   7

Step 607:
2 6 3
1 8 5
4 7  

Step 608:
2 6 3
1 8  
4 7 5

Step 609:
2 6  
1 8 3
4 7 5

Step 610:
2   6
1 8 3
4 7 5

Step 611:
2 8 6
1   3
4 7 5

Step 612:
2 8 6
1 7 3
4   5

Step 613:
2 8 6
1 7 3
4 5  

Step 614:
2 8 6
1 7  
4 5 3

Step 615:
2 8  
1 7 6
4 5 3

Step 616:
2   8
1 7 6
4 5 3

Step 617:
2 7 8
1   6
4 5 3

Step 618:
2 7 8
1 5 6
4   3

Step 619:
2 7 8
1 5 6
4 3  

Step 620:
2 7 8
1 5  
4 3 6

Step 621:
2 7  
1 5 8
4 3 6

Step 622:
2   7
1 5 8
4 3 6

Step 623:
2 5 7
1   8
4 3 6

Step 624:
2 5 7
1 3 8
4   6

Step 625:
2 5 7
1 3 8
4 6  

Step 626:
2 5 7
1 3  
4 6 8

Step 627:
2 5 7
1   3
4 6 8

Step 628:
2 5 7
1 6 3
4   8

Step 629:
2 5 7
1 6 3
4 8  

Step 630:
2 5 7
1 6  
4 8 3

Step 631:
2 5  
1 6 7
4 8 3

Step 632:
2   5
1 6 7
4 8 3

Step 633:
2 6 5
1   7
4 8 3

Step 634:
2 6 5
1 8 7
4   3

Step 635:
2 6 5
1 8 7
4 3  

Step 636:
2 6 5
1 8  
4 3 7

Step 637:
2 6  
1 8 5
4 3 7

Step 638:
2   6
1 8 5
4 3 7

Step 639:
2 8 6
1   5
4 3 7

Step 640:
2 8 6
1 3 5
4   7

Step 641:
2 8 6
1 3 5
  4 7

Step 642:
2 8 6
  3 5
1 4 7

Step 643:
  8 6
2 3 5
1 4 7

Step 644:
8   6
2 3 5
1 4 7

Step 645:
8 3 6
2   5
1 4 7

Step 646:
8 3 6
2 4 5
1   7

Step 647:
8 3 6
2 4 5
  1 7

Step 648:
8 3 6
  4 5
2 1 7

Step 649:
  3 6
8 4 5
2 1 7

Step 650:
3   6
8 4 5
2 1 7

Step 651:
3 4 6
8   5
2 1 7

Step 652:
3 4 6
8 1 5
2   7

Step 653:
3 4 6
8 1 5
2 7  

Step 654:
3 4 6
8 1  
2 7 5

Step 655:
3 4  
8 1 6
2 7 5

Step 656:
3   4
8 1 6
2 7 5

Step 657:
3 1 4
8   6
2 7 5

Step 658:
3 1 4
8 7 6
2   5

Step 659:
3 1 4
8 7 6
2 5  

Step 660:
3 1 4
8 7  
2 5 6

Step 661:
3 1  
8 7 4
2 5 6

Step 662:
3   1
8 7 4
2 5 6

Step 663:
3 7 1
8   4
2 5 6

Step 664:
3 7 1
8 5 4
2   6

Step 665:
3 7 1
8 5 4
2 6  

Step 666:
3 7 1
8 5  
2 6 4

Step 667:
3 7  
8 5 1
2 6 4

Step 668:
3   7
8 5 1
2 6 4

Step 669:
3 5 7
8   1
2 6 4

Step 670:
3 5 7
8 6 1
2   4

Step 671:
3 5 7
8 6 1
2 4  

Step 672:
3 5 7
8 6  
2 4 1

Step 673:
3 5  
8 6 7
2 4 1

Step 674:
3   5
8 6 7
2 4 1

Step 675:
3 6 5
8   7
2 4 1

Step 676:
3 6 5
8 4 7
2   1

Step 677:
3 6 5
8 4 7
2 1  

Step 678:
3 6 5
8 4  
2 1 7

Step 679:
3 6 5
8   4
2 1 7

Step 680:
3 6 5
8 1 4
2   7

Step 681:
3 6 5
8 1 4
2 7  

Step 682:
3 6 5
8 1  
2 7 4

Step 683:
3 6  
8 1 5
2 7 4

Step 684:
3   6
8 1 5
2 7 4

Step 685:
3 1 6
8   5
2 7 4

Step 686:
3 1 6
8 7 5
2   4

Step 687:
3 1 6
8 7 5
2 4  

Step 688:
3 1 6
8 7  
2 4 5

Step 689:
3 1  
8 7 6
2 4 5

Step 690:
3   1
8 7 6
2 4 5

Step 691:
3 7 1
8   6
2 4 5

Step 692:
3 7 1
8 4 6
2   5

Step 693:
3 7 1
8 4 6
  2 5

Step 694:
3 7 1
  4 6
8 2 5

Step 695:
  7 1
3 4 6
8 2 5

Step 696:
7   1
3 4 6
8 2 5

Step 697:
7 4 1
3   6
8 2 5

Step 698:
7 4 1
3 2 6
8   5

Step 699:
7 4 1
3 2 6
8 5  

Step 700:
7 4 1
3 2  
8 5 6

Step 701:
7 4  
3 2 1
8 5 6

Step 702:
7   4
3 2 1
8 5 6

Step 703:
7 2 4
3   1
8 5 6

Step 704:
7 2 4
3 5 1
8   6

Step 705:
7 2 4
3 5 1
8 6  

Step 706:
7 2 4
3 5  
8 6 1

Step 707:
7 2  
3 5 4
8 6 1

Step 708:
7   2
3 5 4
8 6 1

Step 709:
7 5 2
3   4
8 6 1

Step 710:
7 5 2
3 6 4
8   1

Step 711:
7 5 2
3 6 4
8 1  

Step 712:
7 5 2
3 6  
8 1 4

Step 713:
7 5  
3 6 2
8 1 4

Step 714:
7   5
3 6 2
8 1 4

Step 715:
7 6 5
3   2
8 1 4

Step 716:
7 6 5
3 1 2
8   4

Step 717:
7 6 5
3 1 2
8 4  

Step 718:
7 6 5
3 1  
8 4 2

Step 719:
7 6  
3 1 5
8 4 2

Step 720:
7   6
3 1 5
8 4 2

Step 721:
7 1 6
3   5
8 4 2

Step 722:
7 1 6
3 4 5
8   2

Step 723:
7 1 6
3 4 5
8 2  

Step 724:
7 1 6
3 4  
8 2 5

Step 725:
7 1 6
3   4
8 2 5

Step 726:
7 1 6
3 2 4
8   5

Step 727:
7 1 6
3 2 4
8 5  

Step 728:
7 1 6
3 2  
8 5 4

Step 729:
7 1  
3 2 6
8 5 4

Step 730:
7   1
3 2 6
8 5 4

Step 731:
7 2 1
3   6
8 5 4

Step 732:
7 2 1
3 5 6
8   4

Step 733:
7 2 1
3 5 6
8 4  

Step 734:
7 2 1
3 5  
8 4 6

Step 735:
7 2  
3 5 1
8 4 6

Step 736:
7   2
3 5 1
8 4 6

Step 737:
7 5 2
3   1
8 4 6

Step 738:
7 5 2
3 4 1
8   6

Step 739:
7 5 2
3 4 1
  8 6

Step 740:
7 5 2
  4 1
3 8 6

Step 741:
  5 2
7 4 1
3 8 6

Step 742:
5   2
7 4 1
3 8 6

Step 743:
5 4 2
7   1
3 8 6

Step 744:
5 4 2
7 8 1
3   6

Step 745:
5 4 2
7 8 1
3 6  

Step 746:
5 4 2
7 8  
3 6 1

Step 747:
5 4  
7 8 2
3 6 1

Step 748:
5   4
7 8 2
3 6 1

Step 749:
5 8 4
7   2
3 6 1

Step 750:
5 8 4
7 6 2
3   1

Step 751:
5 8 4
7 6 2
3 1  

Step 752:
5 8 4
7 6  
3 1 2

Step 753:
5 8  
7 6 4
3 1 2

Step 754:
5   8
7 6 4
3 1 2

Step 755:
5 6 8
7   4
3 1 2

Step 756:
5 6 8
7 1 4
3   2

Step 757:
5 6 8
7 1 4
3 2  

Step 758:
5 6 8
7 1  
3 2 4

Step 759:
5 6  
7 1 8
3 2 4

Step 760:
5   6
7 1 8
3 2 4

Step 761:
5 1 6
7   8
3 2 4

Step 762:
5 1 6
7 2 8
3   4

Step 763:
5 1 6
7 2 8
3 4  

Step 764:
5 1 6
7 2  
3 4 8

Step 765:
5 1  
7 2 6
3 4 8

Step 766:
5   1
7 2 6
3 4 8

Step 767:
5 2 1
7   6
3 4 8

Step 768:
5 2 1
7 4 6
3   8

Step 769:
5 2 1
7 4 6
3 8  

Step 770:
5 2 1
7 4  
3 8 6

Step 771:
5 2 1
7   4
3 8 6

Step 772:
5 2 1
7 8 4
3   6

Step 773:
5 2 1
7 8 4
3 6  

Step 774:
5 2 1
7 8  
3 6 4

Step 775:
5 2  
7 8 1
3 6 4

Step 776:
5   2
7 8 1
3 6 4

Step 777:
5 8 2
7   1
3 6 4

Step 778:
5 8 2
7 6 1
3   4

Step 779:
5 8 2
7 6 1
3 4  

Step 780:
5 8 2
7 6  
3 4 1

Step 781:
5 8  
7 6 2
3 4 1

Step 782:
5   8
7 6 2
3 4 1

Step 783:
5 6 8
7   2
3 4 1

Step 784:
5 6 8
7 4 2
3   1

Step 785:
5 6 8
7 4 2
  3 1

Step 786:
5 6 8
  4 2
7 3 1

Step 787:
5 6 8
4   2
7 3 1

Step 788:
5 6 8
4 3 2
7   1

Step 789:
5 6 8
4 3 2
7 1  

Step 790:
5 6 8
4 3  
7 1 2

Step 791:
5 6  
4 3 8
7 1 2

Step 792:
5   6
4 3 8
7 1 2

Step 793:
5 3 6
4   8
7 1 2

Step 794:
5 3 6
4 1 8
7   2

Step 795:
5 3 6
4 1 8
7 2  

Step 796:
5 3 6
4 1  
7 2 8

Step 797:
5 3  
4 1 6
7 2 8

Step 798:
5   3
4 1 6
7 2 8

Step 799:
5 1 3
4   6
7 2 8

Step 800:
5 1 3
4 2 6
7   8

Step 801:
5 1 3
4 2 6
7 8  

Step 802:
5 1 3
4 2  
7 8 6

Step 803:
5 1  
4 2 3
7 8 6

Step 804:
5   1
4 2 3
7 8 6

Step 805:
5 2 1
4   3
7 8 6

Step 806:
5 2 1
4 8 3
7   6

Step 807:
5 2 1
4 8 3
7 6  

Step 808:
5 2 1
4 8  
7 6 3

Step 809:
5 2  
4 8 1
7 6 3

Step 810:
5   2
4 8 1
7 6 3

Step 811:
5 8 2
4   1
7 6 3

Step 812:
5 8 2
4 6 1
7   3

Step 813:
5 8 2
4 6 1
7 3  

Step 814:
5 8 2
4 6  
7 3 1

Step 815:
5 8 2
4   6
7 3 1

Step 816:
5 8 2
4 3 6
7   1

Step 817:
5 8 2
4 3 6
7 1  

Step 818:
5 8 2
4 3  
7 1 6

Step 819:
5 8  
4 3 2
7 1 6

Step 820:
5   8
4 3 2
7 1 6

Step 821:
5 3 8
4   2
7 1 6

Step 822:
5 3 8
4 1 2
7   6

Step 823:
5 3 8
4 1 2
7 6  

Step 824:
5 3 8
4 1  
7 6 2

Step 825:
5 3  
4 1 8
7 6 2

Step 826:
5   3
4 1 8
7 6 2

Step 827:
5 1 3
4   8
7 6 2

Step 828:
5 1 3
4 6 8
7   2

Step 829:
5 1 3
4 6 8
  7 2

Step 830:
5 1 3
  6 8
4 7 2

Step 831:
  1 3
5 6 8
4 7 2

Step 832:
1   3
5 6 8
4 7 2

Step 833:
1 6 3
5   8
4 7 2

Step 834:
1 6 3
5 7 8
4   2

Step 835:
1 6 3
5 7 8
4 2  

Step 836:
1 6 3
5 7  
4 2 8

Step 837:
1 6  
5 7 3
4 2 8

Step 838:
1   6
5 7 3
4 2 8

Step 839:
1 7 6
5   3
4 2 8

Step 840:
1 7 6
5 2 3
4   8

Step 841:
1 7 6
5 2 3
4 8  

Step 842:
1 7 6
5 2  
4 8 3

Step 843:
1 7  
5 2 6
4 8 3

Step 844:
1   7
5 2 6
4 8 3

Step 845:
1 2 7
5   6
4 8 3

Step 846:
1 2 7
5 8 6
4   3

Step 847:
1 2 7
5 8 6
4 3  

Step 848:
1 2 7
5 8  
4 3 6

Step 849:
1 2  
5 8 7
4 3 6

Step 850:
1   2
5 8 7
4 3 6

Step 851:
1 8 2
5   7
4 3 6

Step 852:
1 8 2
5 3 7
4   6

Step 853:
1 8 2
5 3 7
4 6  

Step 854:
1 8 2
5 3  
4 6 7

Step 855:
1 8  
5 3 2
4 6 7

Step 856:
1   8
5 3 2
4 6 7

Step 857:
1 3 8
5   2
4 6 7

Step 858:
1 3 8
5 6 2
4   7

Step 859:
1 3 8
5 6 2
4 7  

Step 860:
1 3 8
5 6  
4 7 2

Step 861:
1 3 8
5   6
4 7 2

Step 862:
1 3 8
5 7 6
4   2

Step 863:
1 3 8
5 7 6
4 2  

Step 864:
1 3 8
5 7  
4 2 6

Step 865:
1 3  
5 7 8
4 2 6

Step 866:
1   3
5 7 8
4 2 6

Step 867:
1 7 3
5   8
4 2 6

Step 868:
1 7 3
5 2 8
4   6

Step 869:
1 7 3
5 2 8
4 6  

Step 870:
1 7 3
5 2  
4 6 8

Step 871:
1 7  
5 2 3
4 6 8

Step 872:
1   7
5 2 3
4 6 8

Step 873:
1 2 7
5   3
4 6 8

Step 874:
1 2 7
5 6 3
4   8

Step 875:
1 2 7
5 6 3
  4 8

Step 876:
1 2 7
  6 3
5 4 8

Step 877:
  2 7
1 6 3
5 4 8

Step 878:
2   7
1 6 3
5 4 8

Step 879:
2 6 7
1   3
5 4 8

Step 880:
2 6 7
1 4 3
5   8

Step 881:
2 6 7
1 4 3
5 8  

Step 882:
2 6 7
1 4  
5 8 3

Step 883:
2 6  
1 4 7
5 8 3

Step 884:
2   6
1 4 7
5 8 3

Step 885:
2 4 6
1   7
5 8 3

Step 886:
2 4 6
1 8 7
5   3

Step 887:
2 4 6
1 8 7
5 3  

Step 888:
2 4 6
1 8  
5 3 7

Step 889:
2 4  
1 8 6
5 3 7

Step 890:
2   4
1 8 6
5 3 7

Step 891:
2 8 4
1   6
5 3 7

Step 892:
2 8 4
1 3 6
5   7

Step 893:
2 8 4
1 3 6
5 7  

Step 894:
2 8 4
1 3  
5 7 6

Step 895:
2 8  
1 3 4
5 7 6

Step 896:
2   8
1 3 4
5 7 6

Step 897:
2 3 8
1   4
5 7 6

Step 898:
2 3 8
1 7 4
5   6

Step 899:
2 3 8
1 7 4
5 6  

Step 900:
2 3 8
1 7  
5 6 4

Step 901:
2 3  
1 7 8
5 6 4

Step 902:
2   3
1 7 8
5 6 4

Step 903:
2 7 3
1   8
5 6 4

Step 904:
2 7 3
1 6 8
5   4

Step 905:
2 7 3
1 6 8
5 4  

Step 906:
2 7 3
1 6  
5 4 8

Step 907:
2 7 3
1   6
5 4 8

Step 908:
2 7 3
1 4 6
5   8

Step 909:
2 7 3
1 4 6
5 8  

Step 910:
2 7 3
1 4  
5 8 6

Step 911:
2 7  
1 4 3
5 8 6

Step 912:
2   7
1 4 3
5 8 6

Step 913:
2 4 7
1   3
5 8 6

Step 914:
2 4 7
1 8 3
5   6

Step 915:
2 4 7
1 8 3
5 6  

Step 916:
2 4 7
1 8  
5 6 3

Step 917:
2 4  
1 8 7
5 6 3

Step 918:
2   4
1 8 7
5 6 3

Step 919:
2 8 4
1   7
5 6 3

Step 920:
2 8 4
1 6 7
5   3

Step 921:
2 8 4
1 6 7
  5 3

Step 922:
2 8 4
  6 7
1 5 3

Step 923:
  8 4
2 6 7
1 5 3

Step 924:
8   4
2 6 7
1 5 3

Step 925:
8 6 4
2   7
1 5 3

Step 926:
8 6 4
2 5 7
1   3

Step 927:
8 6 4
2 5 7
  1 3

Step 928:
8 6 4
  5 7
2 1 3

Step 929:
  6 4
8 5 7
2 1 3

Step 930:
6   4
8 5 7
2 1 3

Step 931:
6 5 4
8   7
2 1 3

Step 932:
6 5 4
8 1 7
2   3

Step 933:
6 5 4
8 1 7
2 3  

Step 934:
6 5 4
8 1  
2 3 7

Step 935:
6 5  
8 1 4
2 3 7

Step 936:
6   5
8 1 4
2 3 7

Step 937:
6 1 5
8   4
2 3 7

Step 938:
6 1 5
8 3 4
2   7

Step 939:
6 1 5
8 3 4
2 7  

Step 940:
6 1 5
8 3  
2 7 4

Step 941:
6 1  
8 3 5
2 7 4

Step 942:
6   1
8 3 5
2 7 4

Step 943:
6 3 1
8   5
2 7 4

Step 944:
6 3 1
8 7 5
2   4

Step 945:
6 3 1
8 7 5
2 4  

Step 946:
6 3 1
8 7  
2 4 5

Step 947:
6 3  
8 7 1
2 4 5

Step 948:
6   3
8 7 1
2 4 5

Step 949:
6 7 3
8   1
2 4 5

Step 950:
6 7 3
8 4 1
2   5

Step 951:
6 7 3
8 4 1
2 5  

Step 952:
6 7 3
8 4  
2 5 1

Step 953:
6 7  
8 4 3
2 5 1

Step 954:
6   7
8 4 3
2 5 1

Step 955:
6 4 7
8   3
2 5 1

Step 956:
6 4 7
8 5 3
2   1

Step 957:
6 4 7
8 5 3
2 1  

Step 958:
6 4 7
8 5  
2 1 3

Step 959:
6 4 7
8   5
2 1 3

Step 960:
6 4 7
8 1 5
2   3

Step 961:
6 4 7
8 1 5
2 3  

Step 962:
6 4 7
8 1  
2 3 5

Step 963:
6 4  
8 1 7
2 3 5

Step 964:
6   4
8 1 7
2 3 5

Step 965:
6 1 4
8   7
2 3 5

Step 966:
6 1 4
8 3 7
2   5

Step 967:
6 1 4
8 3 7
2 5  

Step 968:
6 1 4
8 3  
2 5 7

Step 969:
6 1  
8 3 4
2 5 7

Step 970:
6   1
8 3 4
2 5 7

Step 971:
6 3 1
8   4
2 5 7

Step 972:
6 3 1
8 5 4
2   7

Step 973:
6 3 1
8 5 4
  2 7

Step 974:
6 3 1
  5 4
8 2 7

Step 975:
  3 1
6 5 4
8 2 7

Step 976:
3   1
6 5 4
8 2 7

Step 977:
3 5 1
6   4
8 2 7

Step 978:
3 5 1
6 2 4
8   7

Step 979:
3 5 1
6 2 4
8 7  

Step 980:
3 5 1
6 2  
8 7 4

Step 981:
3 5  
6 2 1
8 7 4

Step 982:
3   5
6 2 1
8 7 4

Step 983:
3 2 5
6   1
8 7 4

Step 984:
3 2 5
6 7 1
8   4

Step 985:
3 2 5
6 7 1
8 4  

Step 986:
3 2 5
6 7  
8 4 1

Step 987:
3 2  
6 7 5
8 4 1

Step 988:
3   2
6 7 5
8 4 1

Step 989:
3 7 2
6   5
8 4 1

Step 990:
3 7 2
6 4 5
8   1

Step 991:
3 7 2
6 4 5
8 1  

Step 992:
3 7 2
6 4  
8 1 5

Step 993:
3 7  
6 4 2
8 1 5

Step 994:
3   7
6 4 2
8 1 5

Step 995:
3 4 7
6   2
8 1 5

Step 996:
3 4 7
6 1 2
8   5

Step 997:
3 4 7
6 1 2
8 5  

Step 998:
3 4 7
6 1  
8 5 2

Step 999:
3 4  
6 1 7
8 5 2

Step 1000:
3   4
6 1 7
8 5 2

Step 1001:
3 1 4
6   7
8 5 2

Step 1002:
3 1 4
6 5 7
8   2

Step 1003:
3 1 4
6 5 7
8 2  

Step 1004:
3 1 4
6 5  
8 2 7

Step 1005:
3 1 4
6   5
8 2 7

Step 1006:
3 1 4
6 2 5
8   7

Step 1007:
3 1 4
6 2 5
8 7  

Step 1008:
3 1 4
6 2  
8 7 5

Step 1009:
3 1  
6 2 4
8 7 5

Step 1010:
3   1
6 2 4
8 7 5

Step 1011:
3 2 1
6   4
8 7 5

Step 1012:
3 2 1
6 7 4
8   5

Step 1013:
3 2 1
6 7 4
8 5  

Step 1014:
3 2 1
6 7  
8 5 4

Step 1015:
3 2  
6 7 1
8 5 4

Step 1016:
3   2
6 7 1
8 5 4

Step 1017:
3 7 2
6   1
8 5 4

Step 1018:
3 7 2
6 5 1
8   4

Step 1019:
3 7 2
6 5 1
  8 4

Step 1020:
3 7 2
  5 1
6 8 4

Step 1021:
  7 2
3 5 1
6 8 4

Step 1022:
7   2
3 5 1
6 8 4

Step 1023:
7 5 2
3   1
6 8 4

Step 1024:
7 5 2
3 8 1
6   4

Step 1025:
7 5 2
3 8 1
6 4  

Step 1026:
7 5 2
3 8  
6 4 1

Step 1027:
7 5  
3 8 2
6 4 1

Step 1028:
7   5
3 8 2
6 4 1

Step 1029:
7 8 5
3   2
6 4 1

Step 1030:
7 8 5
3 4 2
6   1

Step 1031:
7 8 5
3 4 2
6 1  

Step 1032:
7 8 5
3 4  
6 1 2

Step 1033:
7 8  
3 4 5
6 1 2

Step 1034:
7   8
3 4 5
6 1 2

Step 1035:
7 4 8
3   5
6 1 2

Step 1036:
7 4 8
3 1 5
6   2

Step 1037:
7 4 8
3 1 5
6 2  

Step 1038:
7 4 8
3 1  
6 2 5

Step 1039:
7 4  
3 1 8
6 2 5

Step 1040:
7   4
3 1 8
6 2 5

Step 1041:
7 1 4
3   8
6 2 5

Step 1042:
7 1 4
3 2 8
6   5

Step 1043:
7 1 4
3 2 8
6 5  

Step 1044:
7 1 4
3 2  
6 5 8

Step 1045:
7 1  
3 2 4
6 5 8

Step 1046:
7   1
3 2 4
6 5 8

Step 1047:
7 2 1
3   4
6 5 8

Step 1048:
7 2 1
3 5 4
6   8

Step 1049:
7 2 1
3 5 4
6 8  

Step 1050:
7 2 1
3 5  
6 8 4

Step 1051:
7 2 1
3   5
6 8 4

Step 1052:
7 2 1
3 8 5
6   4

Step 1053:
7 2 1
3 8 5
6 4  

Step 1054:
7 2 1
3 8  
6 4 5

Step 1055:
7 2  
3 8 1
6 4 5

Step 1056:
7   2
3 8 1
6 4 5

Step 1057:
7 8 2
3   1
6 4 5

Step 1058:
7 8 2
3 4 1
6   5

Step 1059:
7 8 2
3 4 1
6 5  

Step 1060:
7 8 2
3 4  
6 5 1

Step 1061:
7 8  
3 4 2
6 5 1

Step 1062:
7   8
3 4 2
6 5 1

Step 1063:
7 4 8
3   2
6 5 1

Step 1064:
7 4 8
3 5 2
6   1

Step 1065:
7 4 8
3 5 2
  6 1

Step 1066:
7 4 8
  5 2
3 6 1

Step 1067:
  4 8
7 5 2
3 6 1

Step 1068:
4   8
7 5 2
3 6 1

Step 1069:
4 5 8
7   2
3 6 1

Step 1070:
4 5 8
7 6 2
3   1

Step 1071:
4 5 8
7 6 2
3 1  

Step 1072:
4 5 8
7 6  
3 1 2

Step 1073:
4 5  
7 6 8
3 1 2

Step 1074:
4   5
7 6 8
3 1 2

Step 1075:
4 6 5
7   8
3 1 2

Step 1076:
4 6 5
7 1 8
3   2

Step 1077:
4 6 5
7 1 8
3 2  

Step 1078:
4 6 5
7 1  
3 2 8

Step 1079:
4 6  
7 1 5
3 2 8

Step 1080:
4   6
7 1 5
3 2 8

Step 1081:
4 1 6
7   5
3 2 8

Step 1082:
4 1 6
7 2 5
3   8

Step 1083:
4 1 6
7 2 5
3 8  

Step 1084:
4 1 6
7 2  
3 8 5

Step 1085:
4 1  
7 2 6
3 8 5

Step 1086:
4   1
7 2 6
3 8 5

Step 1087:
4 2 1
7   6
3 8 5

Step 1088:
4 2 1
7 8 6
3   5

Step 1089:
4 2 1
7 8 6
3 5  

Step 1090:
4 2 1
7 8  
3 5 6

Step 1091:
4 2  
7 8 1
3 5 6

Step 1092:
4   2
7 8 1
3 5 6

Step 1093:
4 8 2
7   1
3 5 6

Step 1094:
4 8 2
7 5 1
3   6

Step 1095:
4 8 2
7 5 1
3 6  

Step 1096:
4 8 2
7 5  
3 6 1

Step 1097:
4 8 2
7   5
3 6 1

Step 1098:
4 8 2
7 6 5
3   1

Step 1099:
4 8 2
7 6 5
3 1  

Step 1100:
4 8 2
7 6  
3 1 5

Step 1101:
4 8  
7 6 2
3 1 5

Step 1102:
4   8
7 6 2
3 1 5

Step 1103:
4 6 8
7   2
3 1 5

Step 1104:
4 6 8
7 1 2
3   5

Step 1105:
4 6 8
7 1 2
3 5  

Step 1106:
4 6 8
7 1  
3 5 2

Step 1107:
4 6  
7 1 8
3 5 2

Step 1108:
4   6
7 1 8
3 5 2

Step 1109:
4 1 6
7   8
3 5 2

Step 1110:
4 1 6
7 5 8
3   2

Step 1111:
4 1 6
7 5 8
  3 2

Step 1112:
4 1 6
  5 8
7 3 2

Step 1113:
  1 6
4 5 8
7 3 2

Step 1114:
1   6
4 5 8
7 3 2

Step 1115:
1 5 6
4   8
7 3 2

Step 1116:
1 5 6
4 3 8
7   2

Step 1117:
1 5 6
4 3 8
7 2  

Step 1118:
1 5 6
4 3  
7 2 8

Step 1119:
1 5  
4 3 6
7 2 8

Step 1120:
1   5
4 3 6
7 2 8

Step 1121:
1 3 5
4   6
7 2 8

Step 1122:
1 3 5
4 2 6
7   8

Step 1123:
1 3 5
4 2 6
7 8  

Step 1124:
1 3 5
4 2  
7 8 6

Step 1125:
1 3  
4 2 5
7 8 6

Step 1126:
1   3
4 2 5
7 8 6

Step 1127:
1 2 3
4   5
7 8 6

Step 1128:
1 2 3
4 8 5
7   6

Step 1129:
1 2 3
4 8 5
7 6  

Step 1130:
1 2 3
4 8  
7 6 5

Step 1131:
1 2  
4 8 3
7 6 5

Step 1132:
1   2
4 8 3
7 6 5

Step 1133:
1 8 2
4   3
7 6 5

Step 1134:
1 8 2
4 6 3
7   5

Step 1135:
1 8 2
4 6 3
7 5  

Step 1136:
1 8 2
4 6  
7 5 3

Step 1137:
1 8  
4 6 2
7 5 3

Step 1138:
1   8
4 6 2
7 5 3

Step 1139:
1 6 8
4   2
7 5 3

Step 1140:
1 6 8
4 5 2
7   3

Step 1141:
1 6 8
4 5 2
7 3  

Step 1142:
1 6 8
4 5  
7 3 2

Step 1143:
1 6 8
4   5
7 3 2

Step 1144:
1 6 8
4 3 5
7   2

Step 1145:
1 6 8
4 3 5
7 2  

Step 1146:
1 6 8
4 3  
7 2 5

Step 1147:
1 6  
4 3 8
7 2 5

Step 1148:
1   6
4 3 8
7 2 5

Step 1149:
1 3 6
4   8
7 2 5

Step 1150:
1 3 6
4 2 8
7   5

Step 1151:
1 3 6
4 2 8
7 5  

Step 1152:
1 3 6
4 2  
7 5 8

Step 1153:
1 3  
4 2 6
7 5 8

Step 1154:
1   3
4 2 6
7 5 8

Step 1155:
1 2 3
4   6
7 5 8

Step 1156:
1 2 3
4 5 6
7   8

Step 1157:
1 2 3
4 5 6
7 8

Remarks

Breadth-first search (BFS) identifies the optimal solution, 25 moves, in 145,605 iterations.
Depth-first search (DFS) discovers a solution involving 1,157 moves in 1,187 iterations.

How can solutions be discovered more efficiently?

Will Depth-First Search (DFS) invariably yield sub-optimal solutions?

No, if the optimal solution lies along the path traversed by depth-first search (DFS) within the search tree, then DFS will indeed identify the optimal solution.

Is it possible for DFS to discover solutions superior to the optimal solution?

Certainly not; such solutions would either be invalid (involving impossible moves) or indicate an error in your estimation.

Does this imply that depth-first search (DFS) has no practical applications?

When is it appropriate to use DFS?

Breadth-first search (BFS) expands its frontier systematically in all directions, leading to rapid growth in memory requirements.

In contrast, the memory usage of DFS is constrained by the number of moves needed to reach its backtracking points or the path length of the first solution found. In all scenarios, DFS continues expanding the frontier in one direction.

In certain applications where all possible solutions must be explored, the entire search space must be traversed. Using BFS in these cases would be prohibitively expensive in terms of memory. However, DFS can explore the entire space with minimal memory usage.

The programming language Prolog includes a built-in backtracking algorithm that enumerates all possible solutions. Backtracking is a memory-efficient variant of DFS.

Depth-limited and iterative deepening search would be alternative uninformed search algorithms.

Finding solutions more efficiently requires domain knowledge.

Prologue

Summary

Justification for Studying Search
Key Terminology and Concepts
Uninformed Search Algorithms
- Breadth-First Search (BFS)
- Depth-First Search (DFS)
Implementations

Justification for Studying Search:
- Emphasized the shift from solely focusing on machine learning to incorporating search algorithms.
- Highlighted the role of search in advanced AI systems like AlphaGo, AlphaZero, and MuZero.
- Noted that search algorithms are crucial for planning, reasoning, and will be increasingly significant.
Historical Timeline of Search Algorithms:
- Presented a biased timeline from 1968’s A* algorithm to recent developments like MuZero and Agent57.
- Showed the evolution from heuristic-based search to integrating deep learning with search methods.
Applications of Search:
- Pathfinding and Navigation: Finding optimal paths in robotics and games.
- Puzzle Solving: Solving problems like the 8-puzzle and Sudoku.
- Network Analysis: Analyzing connectivity and shortest paths in networks.
- Game Playing: Evaluating moves in games like chess or Go.
- Scheduling and Resource Allocation: Planning tasks and allocating resources efficiently.
- Configuration Problems: Assembling components to meet specific requirements.
- Decision Making under Uncertainty: Making decisions in dynamic and uncertain environments.
- Storytelling: Guiding language models with plans from automated planners.
Key Terminology and Concepts:
- Agent: An entity that performs actions to achieve goals.
- Environment Characteristics: Fully observable, single-agent, deterministic, static, and discrete environments were focused on.
- Search Problem Definition:
  - State Space: All possible states.
  - Initial State: Where the agent starts.
  - Goal State(s): Desired outcome(s).
  - Actions: Possible moves from a state.
  - Transition Model: Rules determining state changes.
  - Action Cost Function: Cost associated with actions.
Uninformed Search Algorithms:
- Breadth-First Search (BFS):
  - Explores the search space level by level.
  - Guarantees the shortest path but can be memory-intensive.
  - Implemented using a queue.
- Depth-First Search (DFS):
  - Explores as deep as possible along each branch before backtracking.
  - Less memory usage but may not find the shortest path.
  - Implemented using a stack.
Implementing Uninformed Search:
- Used the 8-Puzzle as an example problem.
- Represented states as lists of numbers, with 0 as the blank tile.
- Demonstrated BFS and DFS implementations in Python.
- Showed that BFS found the optimal solution in more iterations, while DFS found a suboptimal solution faster.
Limitations of Uninformed Search:
- Inefficient for large or complex problems due to exhaustive nature.
- Lack of domain knowledge leads to unnecessary exploration.

Next lecture

We will further explore heuristic functions and examine additional search algorithms.

References

Russell, Stuart, and Peter Norvig. 2020. Artificial Intelligence: A Modern Approach. 4th ed. Pearson. http://aima.cs.berkeley.edu/.

Schrittwieser, Julian, Ioannis Antonoglou, Thomas Hubert, Karen Simonyan, Laurent Sifre, Simon Schmitt, Arthur Guez, et al. 2020. “Mastering Atari, Go, chess and shogi by planning with a learned model.” Nature 588 (7839): 604–9. https://doi.org/10.1038/s41586-020-03051-4.

Silver, David, Aja Huang, Chris J. Maddison, Arthur Guez, Laurent Sifre, George van den Driessche, Julian Schrittwieser, et al. 2016. “Mastering the game of Go with deep neural networks and tree search.” Nature 529 (7587): 484–89. https://doi.org/10.1038/nature16961.

Simon, Nisha, and Christian Muise. 2024. “Want To Choose Your Own Adventure? Then First Make a Plan.” Proceedings of the Canadian Conference on Artificial Intelligence.

Marcel Turcotte

[email protected]

School of Electrical Engineering and Computer Science (EECS)

University of Ottawa