Introduction aux réseaux de reurones artificiels

CSI 4106 - Automne 2024

Préambule

Citation du Jour

Le Prix Nobel de Physique 2024 a été décerné à John J. Hopfield et Geoffrey E. Hinton “pour leurs découvertes et inventions fondamentales permettant l’apprentissage automatique avec des réseaux de neurones artificiels”

Objectifs d’apprentissage

• Expliquer les perceptrons et MLPs : structure, fonction, histoire, et limitations.
• Décrire les fonctions d’activation : leur rôle dans l’apprentissage de modèles complexes.
• Implémenter un réseau de neurones à propagation avant avec Keras sur Fashion-MNIST.
• Interpréter l’entraînement et les résultats des réseaux neuronaux : visualisation et mesures d’évaluation.
• Se familiariser avec les frameworks d’apprentissage profond : PyTorch, TensorFlow et Keras pour la création et le déploiement de modèles.

Comme mentionné au début de ce cours, il existe deux grandes écoles de pensée en intelligence artificielle : l’IA symbolique et le connexionnisme. Alors que l’approche symbolique dominait initialement le domaine, l’approche connexionniste est désormais la plus répandue. Nous nous concentrerons désormais sur le connexionnisme.

Introduction

Réseaux neuronaux (NN)

Nous concentrons maintenant notre attention sur une famille de modèles d’apprentissage automatique inspirés de la structure et du fonctionnement des réseaux neuronaux biologiques présents chez les animaux.

Aussi appelés réseaux de neurones artificiels ou réseaux neuronaux, abrégés en ANN ou NN.

Apprentissage automatique

• Supervisé: classification, régression

• Non supervisé: autoencodeurs, auto-apprentissage (self-supervised)

• Par renforcement: NN désormais un composant intégral

Nous commencerons notre exploration dans le cadre de l’apprentissage supervisé.

Un neurone

Attribution : Jennifer Walinga, CC BY-SA 4.0

Dans l’étude de l’intelligence artificielle, il est logique de s’inspirer de la forme d’intelligence la mieux comprise : le cerveau humain. Le cerveau est composé d’un réseau complexe de neurones, formant ensemble des réseaux neuronaux biologiques. Bien que chaque neurone présente un comportement relativement simple, il est connecté à des milliers d’autres neurones, contribuant à la fonctionnalité complexe de ces réseaux.

Un neurone peut être conceptualisé comme une unité de calcul basique, et la complexité de la fonction cérébrale découle de l’interconnexion de ces unités.

Yann LeCun et d’autres chercheurs ont souvent noté que les réseaux de neurones artificiels utilisés dans l’apprentissage automatique ressemblent aux réseaux neuronaux biologiques de la même manière que les ailes d’un avion ressemblent à celles d’un oiseau.

Neurones interconnectés

Attribution : Molecular Mechanism of Synaptic Function de l’Institut Médical Howard Hughes (HHMI). Publié sur YouTube le 15-11-2018.

En biologie, nous adoptons essentiellement le concept d’unités de calcul simples interconnectées pour former un réseau qui effectue collectivement des calculs complexes.

Bien que la recherche sur les réseaux neuronaux biologiques soit indéniablement importante, le domaine des réseaux de neurones artificiels n’a incorporé qu’un nombre limité de concepts clés issus de cette recherche.

Connexionniste

Attribution : LeNail, (2019). NN-SVG : Schémas d’Architecture de Réseau Neuronal Prêts à Publier. Journal of Open Source Software, 4(33), 747, https://doi.org/10.21105/joss.00747 (GitHub)

Une autre caractéristique des réseaux neuronaux biologiques que nous adoptons est l’organisation des neurones en couches, particulièrement évidente dans le cortex cérébral.

Le terme “connexionnistes” provient de l’idée que les nœuds dans ces modèles sont interconnectés. Au lieu d’être explicitement programmés, ces modèles apprennent leur comportement par l’entraînement. L’apprentissage profond est une approche connexionniste.

Les réseaux neuronaux (NNs) se composent de couches de nœuds interconnectés (neurones), chaque connexion ayant un poids associé.

Les réseaux neuronaux traitent les données d’entrée à travers ces connexions pondérées, et l’apprentissage se produit en ajustant les poids en fonction des erreurs dans les données d’entraînement.

Hiérarchie des concepts

Attribution : LeCun, Bengio, et Hinton (2015)

Dans le livre “Deep Learning” (Goodfellow, Bengio, et Courville 2016), les auteurs Goodfellow, Bengio et Courville définissent l’apprentissage profond comme un sous-ensemble de l’apprentissage automatique qui permet aux ordinateurs de “comprendre le monde en termes d’une hiérarchie de concepts”.

Cette approche hiérarchique est l’une des contributions les plus significatives de l’apprentissage profond. Elle réduit le besoin d’ingénierie manuelle des attributs et réoriente l’attention vers l’ingénierie des architectures de réseaux neuronaux.

Notions de base

Calculs avec neurodes

où \(x_1, x_2 \in \{0,1\}\) et \(f(z)\) est une fonction indicatrice : \[ f(z)= \begin{cases}0, & z<\theta \\ 1, & z \geq \theta\end{cases} \]

McCulloch et Pitts (1943) a nommé les neurones artificiels, neurodes, pour “neurone” + “nodes” (“nœud”).

En mathématiques, \(f(z)\), tel que défini ci-dessus, est connu sous le nom de fonction indicatrice ou de fonction caractéristique.

Ces neurodes ont une ou plusieurs entrées binaires, prenant une valeur de 0 ou 1, et une sortie binaire.

Ils ont montré que de telles unités pouvaient implémenter des fonctions booléennes telles que ET, OU, et NON.

Mais aussi que les réseaux de telles unités peuvent calculer toute proposition logique.

Calculs avec neurodes

\[ y = f(x_1 + x_2)= \begin{cases}0, & x_1 + x_2 <\theta \\ 1, & x_1 + x_2 \geq \theta\end{cases} \]

• Avec \(\theta = 2\), le neurode implémente une porte logique ET.

• Avec \(\theta = 1\), le neurode implémente une porte logique OU.

Une logique plus complexe peut être construite en multipliant les entrées par -1, ce qui est interprété comme inhibiteur. Cela permet notamment de construire une logique NON.

Avec \(\theta = 1\), si \(x_1 \in \{1\}\) et que \(x_2\) est multiplié par (-1), \(y = 0\) lorsque \(x_2 = 1\), et \(y = 1\) lorsque \(x_2 = 0\).

\[ y = f(x_1 + (-1) x_2)= \begin{cases}0, & x_1 + (-1) x_2 <\theta \\ 1, & x_1 + (-1) x_2 \geq \theta\end{cases} \]

Les neurones peuvent être classés en deux grandes catégories : excitateur et inhibiteur.

Calculs avec neurodes

• Les calculs numériques peuvent être décomposés en une suite d’opérations logiques, permettant aux réseaux de neurodes d’exécuter tout calcul.

• McCulloch et Pitts (1943) ne se sont pas concentrés sur l’apprentissage du paramètre \(\theta\).

• Ils ont introduit une machine qui calcule toute fonction, mais ne peut pas apprendre.

De ces travaux, nous retenons l’idée que les réseaux de telles unités effectuent des calculs. Le signal se propage d’un bout du réseau pour produire un résultat.

Unité logique à seuil

Rosenblatt (1958)

En 1957, Frank Rosenblatt a développé un modèle conceptuellement distinct de neurone appelé unité logique à seuil (threshold logic unit), qu’il a publié en 1958.

Dans ce modèle, les entrées et la sortie du neurone sont représentées par des valeurs réelles. Notamment, chaque connexion d’entrée a un poids associé.

La partie gauche du neurone, représentée par le symbole sigma, représente le calcul d’une somme pondérée de ses entrées, exprimée comme \(\theta_1 x_1 + \theta_2 x_2 + \ldots + \theta_D x_D + b\).

Cette somme est ensuite traitée par une fonction de seuil pour générer la sortie.

Ici, \(x^T \theta\) représente le produit scalaire de deux vecteurs : \(x\) et \(\theta\). \(x^T\) désigne la transposée du vecteur \(x\), le convertissant d’un vecteur ligne à un vecteur colonne, permettant l’opération du produit scalaire avec le vecteur \(\theta\).

Le produit scalaire \(x^T \theta\) est alors un scalaire donné par :

\[ x^T \theta = x^{(1)} \theta_1 + x^{(2)} \theta_2 + \cdots + x_{(D)} \theta_D \]

où \(x^{(j)}\) et \(theta_j\) sont les composantes des vecteurs \(x\) et \(\theta\), respectivement.

Fonctions de seuil simples

\(\text{heaviside}(t)\) =

• 1, si \(t \geq 0\)

• 0, si \(t < 0\)

\(\text{sign}(t)\) =

• 1, si \(t > 0\)

• 0, si \(t = 0\)

• -1, si \(t < 0\)

Les fonctions de seuil courantes incluent la fonction heaviside (0 si l’entrée est négative et 1 sinon) ou la fonction sign (-1 si l’entrée est négative, 0 si l’entrée est égale à zéro, 1 sinon).

Notation

Ajoutez un attribut supplémentaire avec une valeur fixe de 1 à l’entrée. Associez-la à un poids \(b = \theta_{0}\), où \(b\) est le biais/interception.

Notation

\(\theta_{0} = b\) est le terme de biais/interception.

L’unité logique à seuil est analogue à la régression logistique, la principale différence étant la substitution de la fonction logistique (sigmoïde) par une fonction de seuil. Comme la régression logistique, le perceptron est utilisé pour les tâches de classification.

Perceptron

Un perceptron est constitué d’une ou plusieurs unités logiques à seuil disposées en une seule couche, chaque unité étant connectée à toutes les entrées. Cette configuration est appelée complètement connectée (fully connected) ou dense.

Puisque les unités logiques à seuil dans cette couche unique génèrent également la sortie, on l’appelle couche de sortie.

Perceptron

Comme ce perceptron génère plusieurs sorties simultanément, il effectue des prédictions binaires multiples, ce qui en fait un classificateur multilabel (peut aussi être utilisé comme classificateur multiclass).

Les tâches de classification peuvent être divisées en classification multilabel et classification multiclass.

1. Classification multiclass :

   • Dans la classification multiclass, chaque instance est assignée à une seule classe parmi trois ou plus classes possibles. Les classes sont mutuellement exclusives, ce qui signifie qu’une instance ne peut pas appartenir à plusieurs classes en même temps.

   • Exemple : Classer une image comme étant soit un chat, un chien, ou un oiseau. Chaque image appartient à une seule de ces catégories.

2. Classification multilabel :

   • Dans la classification multilabel, chaque instance peut être associée à plusieurs classes simultanément. Les classes ne sont pas mutuellement exclusives, permettant ainsi qu’une instance appartienne à plusieurs classes à la fois.

   • Exemple : Attribuer des balises à une image telles que “extérieur”, “coucher de soleil”, et “plage”. L’image peut appartenir simultanément à toutes ces étiquettes.

La différence clé réside dans la relation entre les classes : la classification multiclass traite d’une seule étiquette par instance, tandis que la classification multilabel gère plusieurs étiquettes pour chaque instance.

Notation

Comme précédemment, introduisez un attribut supplémentaire avec une valeur de 1 à l’entrée. Attribuez un biais \(b\) à chaque neurone. Chaque connexion entrante a implicitement un poids associé.

Notation

• \(X\) est la matrice de données d’entrée où chaque ligne correspond à un exemple et chaque colonne représente l’un des \(D\) attributs.

• \(W\) est la matrice de poids, structurée avec une ligne par entrée (attribut) et une colonne par neurone.

• Les termes de biais peuvent être représentés séparément ; les deux approches apparaissent dans la littérature. Ici, \(b\) est un vecteur de longueur égale au nombre de neurones.

Avec les réseaux neuronaux, les paramètres du modèle sont souvent désignés par \(w\) (vecteur) ou \(W\) (matrice), plutôt que par \(\theta\).

Discussion

• L’algorithme pour entraîner le perceptron ressemble étroitement à la descente de gradient stochastique.

  • Dans l’intérêt du temps et pour éviter la confusion, nous passerons cet algorithme et nous nous concentrerons sur le perceptron multicouche (MLP) et son algorithme d’entraînement, le backpropagation.

Note historique et justification

Minsky et Papert (1969) a démontré les limites des perceptrons, notamment leur incapacité à résoudre les problèmes de classification OU exclusif (XOR) : \({([0,1],\mathrm{true}), ([1,0],\mathrm{true}), ([0,0],\mathrm{false}), ([1,1],\mathrm{false})}\).

Cette limitation s’applique également à d’autres classificateurs linéaires, tels que la régression logistique.

En conséquence, en raison de ces limitations et du manque d’applications pratiques à l’époque, certains chercheurs ont abandonné les perceptrons.

Perceptron multicouche (MLP)

Un perceptron multicouche (MLP) inclut une couche d’entrée et une ou plusieurs couches d’unités logiques à seuil. Les couches qui ne sont ni d’entrée ni de sortie sont appelées couches cachées.

Problème de classification XOR

\(x^{(1)}\)	\(x^{(2)}\)	\(y\)	\(o_1\)	\(o_2\)	\(o_3\)
1	0	1	0	1	1
0	1	1	0	1	1
0	0	0	0	0	0
1	1	0	1	1	0

\(x^{(1)}\) et \(x^{(2)}\) sont deux attributs, \(y\) est la cible, \(o_1\), \(o_2\), et \(o_3 = h_\theta(x)\), sont les sorties des unités logiques à seuil en haut à gauche, en bas à gauche, et à droite. Clairement, \(h_\theta(x) = y, \forall x \in X\). Le défi à l’époque de Rosenblatt résidait dans l’absence d’algorithmes pour entraîner des réseaux à couches multiples.

J’ai développé un tableur Excel pour vérifier que le perceptron multicouche proposé résout effectivement le problème de classification XOR.

La fonction de seuil utilisée dans ce modèle est la fonction de Heaviside.

Propagation avant (FNN)

Dans cette architecture, l’information circule dans une seule direction — de gauche à droite, passant de l’entrée à la sortie. Cela lui vaut le nom de réseau de neurones à propagation avant (feedforward network – FNN).

Le réseau est constitué de trois couches : d’entrée, cachée et de sortie. La couche d’entrée contient deux nœuds, la couche cachée comprend trois nœuds, et la couche de sortie a deux nœuds. Des couches cachées supplémentaires et des nœuds par couche peuvent être ajoutés, ce qui sera discuté plus tard.

Il est souvent utile d’inclure des nœuds d’entrée explicites qui ne réalisent aucun calcul, appelés unités d’entrée ou neurones d’entrée. Ces nœuds agissent comme des espaces réservés pour introduire des attributs d’entrée dans le réseau, transmettant les données directement à la couche suivante sans transformation. Dans le diagramme du réseau, ce sont les nœuds bleu clair à gauche, étiquetés 1 et 2. Typiquement, le nombre d’unités d’entrée correspond au nombre d’attributs.

Pour plus de clarté, les nœuds sont étiquetés pour faciliter la discussion des poids entre eux, tels que \(w_{1,5}\) entre les nœuds 1 et 5. De même, la sortie d’un nœud est désignée par \(o_k\), où \(k\) représente l’étiquette du nœud. Par exemple, pour \(k=3\), la sortie serait \(o_3\).

Propagation avant (Calcul)

\(o_3 = \sigma(w_{13} x^{(1)}+ w_{23} x^{(2)} + b_3)\)

\(o_4 = \sigma(w_{14} x^{(1)}+ w_{24} x^{(2)} + b_4)\)

\(o_5 = \sigma(w_{15} x^{(1)}+ w_{25} x^{(2)} + b_5)\)

\(o_6 = \sigma(w_{36} o_3 + w_{46} o_4 + w_{56} o_5 + b_6)\)

\(o_7 = \sigma(w_{37} o_3 + w_{47} o_4 + w_{57} o_5 + b_7)\)

Il est important de comprendre le flux d’information : ce réseau calcule deux sorties à partir de ses entrées.

Pour simplifier la figure, j’ai choisi de ne pas afficher les termes de biais, bien qu’ils restent des composants cruciaux. Plus précisément, \(b_3\) représente le terme de biais associé au nœud 3.

Si les termes de biais n’étaient pas significatifs, le processus d’entraînement les réduirait naturellement à zéro. Les termes de biais sont essentiels car ils permettent d’ajuster la frontière de décision, permettant ainsi au modèle d’apprendre des schémas plus complexes que les poids seuls ne peuvent capturer. En offrant des degrés de liberté supplémentaires, ils contribuent également à une convergence plus rapide pendant l’entraînement.

Propagation avant (Calcul)

import numpy as np

# Fonction sigmoïde

def sigma(x):
    return 1 / (1 + np.exp(-x))

# Vecteur d'entrée (deux attributs), un exemple de notre ensemble d'entraînement

x1, x2 = (0.5, 0.9)

# Initialisation des poids des couches 2 et 3 à des valeurs aléatoires

w13, w14, w15, w23, w24, w25 = np.random.uniform(low=-1, high=1, size=6)
w36, w46, w56, w37, w47, w57 = np.random.uniform(low=-1, high=1, size=6)

# Initialisation des 5 termes de biais à des valeurs aléatoires

b3, b4, b5, b6, b7 = np.random.uniform(low=-1, high=1, size=5)

o3 = sigma(w13 * x1 + w23 * x2 + b3)
o4 = sigma(w14 * x1 + w24 * x2 + b4)
o5 = sigma(w15 * x1 + w25 * x2 + b5)
o6 = sigma(w36 * o3 + w46 * o4 + w56 * o5 + b6)
o7 = sigma(w37 * o3 + w47 * o4 + w57 * o5 + b7)

(o6, o7)

(0.8147477393195509, 0.2005628062986649)

L’exemple ci-dessus illustre le processus de calcul avec des valeurs spécifiques. Avant d’entraîner un réseau de neurones, il est courant d’initialiser les poids et les biais avec des valeurs aléatoires. La descente de gradient est ensuite utilisée pour ajuster itérativement ces paramètres afin de minimiser la fonction de perte.

Propagation avant (Calcul)

Le flux d’information reste cohérent même dans des réseaux plus complexes. Les réseaux avec de nombreuses couches sont appelés réseaux de neurones profonds (DNN).

Produit avec NN-SVG, LeNail (2019).

Propagation avant (Calcul)

Même réseau avec termes de biais montrés.

Produit avec NN-SVG, LeNail (2019).

Fonction d’activation

• Comme discuté plus tard, l’algorithme d’entraînement, appelé rétropropagation (backpropagation), utilise la descente de gradient, nécessitant le calcul des dérivées partielles de la fonction de perte.

• La fonction de seuil dans le perceptron multicouche a dû être remplacée, car elle consiste uniquement en des surfaces plates. La descente de gradient ne peut pas progresser sur des surfaces planes en raison de leur dérivée nulle.

Fonction d’activation

• Les fonctions d’activation non linéaires sont primordiales car, sans elles, plusieurs couches du réseau ne calculeraient qu’une fonction linéaire des entrées.

• Selon le théorème d’approximation universelle, des réseaux profonds suffisamment grands avec des fonctions d’activation non linéaires peuvent approximer n’importe quelle fonction continue. Voir Théorème d’Approximation Universelle.

Sigmoïde

\[ \sigma(t) = \frac{1}{1 + e^{-t}} \]

Fonction tangente hyperbolique

\[ \tanh(t) = 2 \sigma(2t) - 1 \]

Cette courbe en forme de S, semblable à la fonction sigmoïde, produit des valeurs de sortie allant de -1 à 1. Selon Géron (2022), cette plage permet à la sortie de chaque couche d’être approximativement centrée autour de 0 au début de l’entraînement, accélérant ainsi la convergence.

Fonction unitaire rectifiée (ReLU)

\[ \mathrm{ReLU}(t) = \max(0, t) \]

Bien que la fonction ReLU ne soit pas différentiable en \(t=0\) et qu’elle ait une dérivée nulle pour \(t<0\), elle fonctionne remarquablement bien en pratique et est très efficace d’un point de vue computationnel. Par conséquent, elle est devenue la fonction d’activation par défaut.

Fonctions d’activation courantes

Géron (2022) – 10_neural_nets_with_keras.ipynb

Approximation Universelle

Définition

Le théorème d’approximation universelle affirme qu’un réseau de neurones feedforward avec une seule couche cachée contenant un nombre fini de neurones peut approcher n’importe quelle fonction continue sur un sous-ensemble compact de \(\mathbb{R}^n\), avec des poids et des fonctions d’activation appropriés.

Cybenko (1989); Hornik, Stinchcombe, et White (1989)

En termes mathématiques, un sous-ensemble de \(\mathbb{R}^n\) est considéré comme compact s’il est à la fois fermé et borné.

• Fermé : Un ensemble est fermé s’il contient tous ses points limites. En d’autres termes, il inclut ses points d’accumulation.

• Borné : Un ensemble est borné s’il existe un nombre réel \(M\) tel que la distance entre deux points quelconques de l’ensemble soit inférieure à \(M\).

Dans le contexte du théorème d’approximation universelle, la compacité garantit que la fonction à approximer est définie sur une région finie et bien comportée, ce qui est crucial pour les garanties théoriques fournies par le théorème.

Démonstration par le code

import numpy as np

# Définition de la fonction à approximer

def f(x):
    return 2 * x**3 + 4 * x**2 - 5 * x + 1

# Génération d'un jeu de données, x dans [-4,2), f(x) comme ci-dessus

X = 6 * np.random.rand(1000, 1) - 4

y = f(X.flatten())

Augmenter le nombre de neurones

from sklearn.neural_network import MLPRegressor
from sklearn.model_selection import train_test_split

X_train, X_valid, y_train, y_valid = train_test_split(X, y, test_size=0.1, random_state=42)

models = []

sizes = [1, 2, 5, 10, 100]

for i, n in enumerate(sizes):

    models.append(MLPRegressor(hidden_layer_sizes=[n], max_iter=5000, random_state=42))

    models[i].fit(X_train, y_train)

MLPRegressor est un régresseur perceptron multicouche de sklearn. Sa fonction d’activation par défaut est relu.

Augmenter le nombre de neurones

Dans l’exemple ci-dessus, j’ai conservé seulement 10% des données comme ensemble de test car la fonction à approximer est simple et sans bruit. Cette décision a été prise pour s’assurer que la courbe réelle ne masque pas les autres résultats.

Augmenter le nombre de neurones

Comme prévu, augmenter le nombre de neurones réduit la perte.

Approximation Universelle

Cette vidéo transmet efficacement l’intuition sous-jacente du théorème d’approximation universelle. (18m 53s)

La vidéo élucide efficacement les concepts clés (terminologie) des réseaux neuronaux, y compris les nœuds, les couches, les poids et les fonctions d’activation. Elle démontre le processus de sommation des sorties d’activation d’une couche précédente, semblable à l’agrégation de courbes. De plus, la vidéo illustre comment la mise à l’échelle d’une sortie par un poids modifie non seulement l’amplitude d’une courbe, mais inverse également son orientation lorsque le poids est négatif. En outre, elle décrit clairement la fonction des termes de biais dans le déplacement vertical de la courbe, en fonction du signe du biais.

Codons

Bibliothèques

PyTorch et TensorFlow sont les plateformes dominantes pour l’apprentissage profond.

• PyTorch a gagné beaucoup de traction dans la communauté de recherche. Initialement développé par Meta AI, il fait maintenant partie de la Linux Foundation.

• TensorFlow, créé par Google, est largement adopté dans l’industrie pour déployer des modèles en production.

Keras

Keras est une API de haut niveau conçue pour construire, entraîner, évaluer et exécuter des modèles sur diverses plateformes, y compris PyTorch, TensorFlow et JAX, la plateforme haute performance de Google.

Keras est suffisamment puissant pour la plupart des projets.

Comme mentionné dans des citations du jour précédentes, François Chollet, un ingénieur chez Google, est l’initiateur et l’un des principaux développeurs du projet Keras.

Dataset Fashion-MNIST

“Fashion-MNIST est un ensemble de données d’images d’articles de Zalando — comprenant un ensemble d’entraînement de 60 000 exemples et un ensemble de test de 10 000 exemples. Chaque exemple est une image en niveaux de gris de 28x28, associée à une étiquette provenant de 10 classes.”

Attribution : Géron (2022) – 10_neural_nets_with_keras.ipynb

Chargement

import tensorflow as tf

fashion_mnist = tf.keras.datasets.fashion_mnist.load_data()

(X_train_full, y_train_full), (X_test, y_test) = fashion_mnist

X_train, y_train = X_train_full[:-5000], y_train_full[:-5000]
X_valid, y_valid = X_train_full[-5000:], y_train_full[-5000:]

Mise de côté de 5000 exemples pour constituer un ensemble de validation.

Exploration

X_train.shape

(55000, 28, 28)

. . .

Transformer les intensités des pixels d’entiers dans la plage de 0 à 255 en flottants dans la plage de 0 à 1.

X_train, X_valid, X_test = X_train / 255., X_valid / 255., X_test / 255.

À quoi ressemblent ces images ?

plt.figure(figsize=(2, 2))
plt.imshow(X_train[0], cmap="binary")
plt.axis('off')
plt.show()

. . .

y_train

array([9, 0, 0, ..., 9, 0, 2], dtype=uint8)

. . .

Puisque les étiquettes sont des entiers de 0 à 9, les noms des classes seront utiles.

class_names = ["T-shirt/top", "Pantalon", "Pull", "Robe", "Manteau",
               "Sandale", "Chemise", "Basket", "Sac", "Botte"]

Les 40 premières images

n_rows = 4
n_cols = 10
plt.figure(figsize=(n_cols * 1.2, n_rows * 1.2))
for row in range(n_rows):
    for col in range(n_cols):
        index = n_cols * row + col
        plt.subplot(n_rows, n_cols, index + 1)
        plt.imshow(X_train[index], cmap="binary", interpolation="nearest")
        plt.axis('off')
        plt.title(class_names[y_train[index]])
plt.subplots_adjust(wspace=0.2, hspace=0.5)
plt.show()

Création d’un modèle

tf.random.set_seed(42)

model = tf.keras.Sequential()

model.add(tf.keras.layers.InputLayer(shape=[28, 28]))
model.add(tf.keras.layers.Flatten())
model.add(tf.keras.layers.Dense(300, activation="relu"))
model.add(tf.keras.layers.Dense(100, activation="relu"))
model.add(tf.keras.layers.Dense(10, activation="softmax"))

model.summary()

Model: "sequential"

┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━┓
┃ Layer (type)                    ┃ Output Shape           ┃       Param # ┃
┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━┩
│ flatten (Flatten)               │ (None, 784)            │             0 │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ dense (Dense)                   │ (None, 300)            │       235,500 │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ dense_1 (Dense)                 │ (None, 100)            │        30,100 │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ dense_2 (Dense)                 │ (None, 10)             │         1,010 │
└─────────────────────────────────┴────────────────────────┴───────────────┘

 Total params: 266,610 (1.02 MB)

 Trainable params: 266,610 (1.02 MB)

 Non-trainable params: 0 (0.00 B)

Comme observé, dense_3 possède \(235,500\) paramètres, tandis que \(784 \times 300 = 235,200\).

Pouvez-vous expliquer l’origine des paramètres supplémentaires ?

De même, dense_3 a \(30,100\) paramètres, tandis que \(300 \times 100 = 30,000\).

Pouvez-vous expliquer pourquoi ?

Création d’un modèle (alternative)

model = tf.keras.Sequential([
    tf.keras.layers.Flatten(input_shape=[28, 28]),
    tf.keras.layers.Dense(300, activation="relu"),
    tf.keras.layers.Dense(100, activation="relu"),
    tf.keras.layers.Dense(10, activation="softmax")
])

model.summary()

Model: "sequential"

┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━┓
┃ Layer (type)                    ┃ Output Shape           ┃       Param # ┃
┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━┩
│ flatten (Flatten)               │ (None, 784)            │             0 │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ dense (Dense)                   │ (None, 300)            │       235,500 │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ dense_1 (Dense)                 │ (None, 100)            │        30,100 │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ dense_2 (Dense)                 │ (None, 10)             │         1,010 │
└─────────────────────────────────┴────────────────────────┴───────────────┘

 Total params: 266,610 (1.02 MB)

 Trainable params: 266,610 (1.02 MB)

 Non-trainable params: 0 (0.00 B)

Compilation du modèle

model.compile(loss="sparse_categorical_crossentropy",
              optimizer="sgd",
              metrics=["accuracy"])

sparse_categorical_crossentropy est la fonction de perte appropriée pour un problème de classification multiclasses (plus de détails à venir).

La méthode compile permet de définir la fonction de perte, ainsi que d’autres paramètres. Keras prépare ensuite le modèle pour l’entraînement.

Entraînement du modèle

history = model.fit(X_train, y_train, epochs=30,
                    validation_data=(X_valid, y_valid))

Epoch 1/30
   1/1719 ━━━━━━━━━━━━━━━━━━━━ 4:06 143ms/step - accuracy: 0.1562 - loss: 2.2538   2/1719 ━━━━━━━━━━━━━━━━━━━━ 2s 2ms/step - accuracy: 0.1406 - loss: 2.2523      64/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 827us/step - accuracy: 0.3202 - loss: 2.0611  65/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 828us/step - accuracy: 0.3223 - loss: 2.0583 129/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 808us/step - accuracy: 0.4127 - loss: 1.8961 130/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 809us/step - accuracy: 0.4136 - loss: 1.8938 196/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 796us/step - accuracy: 0.4652 - loss: 1.7622 259/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 795us/step - accuracy: 0.4991 - loss: 1.6623 261/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 796us/step - accuracy: 0.5000 - loss: 1.6595 260/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 797us/step - accuracy: 0.4996 - loss: 1.6609 320/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 807us/step - accuracy: 0.5234 - loss: 1.5836 321/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 808us/step - accuracy: 0.5238 - loss: 1.5824 378/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 820us/step - accuracy: 0.5419 - loss: 1.5207 379/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 821us/step - accuracy: 0.5422 - loss: 1.5197 435/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 832us/step - accuracy: 0.5570 - loss: 1.4679 491/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 841us/step - accuracy: 0.5697 - loss: 1.4226 547/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 846us/step - accuracy: 0.5808 - loss: 1.3828 548/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 847us/step - accuracy: 0.5810 - loss: 1.3821 603/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 853us/step - accuracy: 0.5906 - loss: 1.3473 604/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 854us/step - accuracy: 0.5908 - loss: 1.3467 662/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 855us/step - accuracy: 0.5999 - loss: 1.3138 663/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 855us/step - accuracy: 0.6000 - loss: 1.3133 719/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 859us/step - accuracy: 0.6080 - loss: 1.2845 720/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 860us/step - accuracy: 0.6081 - loss: 1.2840 776/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 862us/step - accuracy: 0.6154 - loss: 1.2579 777/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 863us/step - accuracy: 0.6155 - loss: 1.2574 836/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 862us/step - accuracy: 0.6226 - loss: 1.2321 837/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 862us/step - accuracy: 0.6227 - loss: 1.2317 903/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 855us/step - accuracy: 0.6299 - loss: 1.2059 904/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 855us/step - accuracy: 0.6300 - loss: 1.2056 974/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 846us/step - accuracy: 0.6369 - loss: 1.1805 975/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 846us/step - accuracy: 0.6370 - loss: 1.18011045/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 837us/step - accuracy: 0.6434 - loss: 1.15711046/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 837us/step - accuracy: 0.6435 - loss: 1.15681115/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 831us/step - accuracy: 0.6493 - loss: 1.13601116/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 831us/step - accuracy: 0.6494 - loss: 1.13571181/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 828us/step - accuracy: 0.6544 - loss: 1.11761182/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 828us/step - accuracy: 0.6545 - loss: 1.11741252/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 822us/step - accuracy: 0.6595 - loss: 1.09931253/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 822us/step - accuracy: 0.6595 - loss: 1.09911321/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 818us/step - accuracy: 0.6641 - loss: 1.08281322/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 818us/step - accuracy: 0.6642 - loss: 1.08251390/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 814us/step - accuracy: 0.6684 - loss: 1.06721391/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 814us/step - accuracy: 0.6685 - loss: 1.06701462/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 809us/step - accuracy: 0.6727 - loss: 1.05201535/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 803us/step - accuracy: 0.6767 - loss: 1.03751534/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 803us/step - accuracy: 0.6767 - loss: 1.03751536/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 803us/step - accuracy: 0.6768 - loss: 1.03731607/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 799us/step - accuracy: 0.6805 - loss: 1.02411608/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 799us/step - accuracy: 0.6805 - loss: 1.02391681/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 795us/step - accuracy: 0.6841 - loss: 1.01111719/1719 ━━━━━━━━━━━━━━━━━━━━ 2s 869us/step - accuracy: 0.6859 - loss: 1.0045 - val_accuracy: 0.8294 - val_loss: 0.5037
Epoch 2/30
   1/1719 ━━━━━━━━━━━━━━━━━━━━ 18s 11ms/step - accuracy: 0.8438 - loss: 0.5045   2/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 817us/step - accuracy: 0.8438 - loss: 0.4920  75/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 687us/step - accuracy: 0.8288 - loss: 0.5051 145/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 701us/step - accuracy: 0.8194 - loss: 0.5216 146/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 700us/step - accuracy: 0.8193 - loss: 0.5217 216/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 707us/step - accuracy: 0.8164 - loss: 0.5258 285/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 713us/step - accuracy: 0.8159 - loss: 0.5265 286/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 715us/step - accuracy: 0.8159 - loss: 0.5265 355/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 718us/step - accuracy: 0.8158 - loss: 0.5266 424/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 719us/step - accuracy: 0.8158 - loss: 0.5263 425/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 720us/step - accuracy: 0.8158 - loss: 0.5263 497/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 717us/step - accuracy: 0.8159 - loss: 0.5256 498/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 717us/step - accuracy: 0.8159 - loss: 0.5256 499/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 717us/step - accuracy: 0.8159 - loss: 0.5256 571/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 715us/step - accuracy: 0.8162 - loss: 0.5249 572/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 715us/step - accuracy: 0.8162 - loss: 0.5249 642/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 715us/step - accuracy: 0.8166 - loss: 0.5241 643/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 715us/step - accuracy: 0.8166 - loss: 0.5240 714/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 715us/step - accuracy: 0.8170 - loss: 0.5231 715/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 715us/step - accuracy: 0.8170 - loss: 0.5231 788/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 713us/step - accuracy: 0.8174 - loss: 0.5222 861/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 711us/step - accuracy: 0.8179 - loss: 0.5212 862/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 711us/step - accuracy: 0.8179 - loss: 0.5212 932/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 711us/step - accuracy: 0.8184 - loss: 0.52021001/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 712us/step - accuracy: 0.8188 - loss: 0.51911002/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 713us/step - accuracy: 0.8188 - loss: 0.51911072/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 713us/step - accuracy: 0.8192 - loss: 0.51791073/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 714us/step - accuracy: 0.8192 - loss: 0.51791143/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 714us/step - accuracy: 0.8197 - loss: 0.51681144/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 714us/step - accuracy: 0.8197 - loss: 0.51681216/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 713us/step - accuracy: 0.8201 - loss: 0.51581292/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 710us/step - accuracy: 0.8205 - loss: 0.51481293/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 710us/step - accuracy: 0.8205 - loss: 0.51481364/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 710us/step - accuracy: 0.8209 - loss: 0.51381365/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 711us/step - accuracy: 0.8209 - loss: 0.51381436/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 710us/step - accuracy: 0.8213 - loss: 0.51281437/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 710us/step - accuracy: 0.8213 - loss: 0.51281511/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 709us/step - accuracy: 0.8217 - loss: 0.51181583/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 708us/step - accuracy: 0.8221 - loss: 0.51091584/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 709us/step - accuracy: 0.8221 - loss: 0.51091658/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 707us/step - accuracy: 0.8225 - loss: 0.50991719/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 746us/step - accuracy: 0.8227 - loss: 0.5092 - val_accuracy: 0.8392 - val_loss: 0.4520
Epoch 3/30
   1/1719 ━━━━━━━━━━━━━━━━━━━━ 18s 11ms/step - accuracy: 0.8750 - loss: 0.4578  76/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 667us/step - accuracy: 0.8506 - loss: 0.4391  77/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 670us/step - accuracy: 0.8505 - loss: 0.4393 152/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 669us/step - accuracy: 0.8422 - loss: 0.4566 153/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 670us/step - accuracy: 0.8421 - loss: 0.4567 225/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 680us/step - accuracy: 0.8395 - loss: 0.4610 226/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 681us/step - accuracy: 0.8395 - loss: 0.4611 300/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 682us/step - accuracy: 0.8386 - loss: 0.4626 301/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 683us/step - accuracy: 0.8385 - loss: 0.4626 372/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 688us/step - accuracy: 0.8383 - loss: 0.4631 373/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 689us/step - accuracy: 0.8382 - loss: 0.4631 447/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 687us/step - accuracy: 0.8380 - loss: 0.4635 448/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 688us/step - accuracy: 0.8380 - loss: 0.4635 518/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 692us/step - accuracy: 0.8380 - loss: 0.4634 519/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 692us/step - accuracy: 0.8380 - loss: 0.4634 592/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 692us/step - accuracy: 0.8382 - loss: 0.4633 664/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 693us/step - accuracy: 0.8385 - loss: 0.4629 665/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 693us/step - accuracy: 0.8385 - loss: 0.4629 736/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 694us/step - accuracy: 0.8388 - loss: 0.4625 809/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 694us/step - accuracy: 0.8391 - loss: 0.4621 810/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 695us/step - accuracy: 0.8392 - loss: 0.4621 882/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 695us/step - accuracy: 0.8395 - loss: 0.4617 955/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 694us/step - accuracy: 0.8398 - loss: 0.4612 956/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 695us/step - accuracy: 0.8398 - loss: 0.46121028/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 695us/step - accuracy: 0.8402 - loss: 0.46051101/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 695us/step - accuracy: 0.8405 - loss: 0.45981102/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 695us/step - accuracy: 0.8405 - loss: 0.45981174/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 695us/step - accuracy: 0.8408 - loss: 0.45921175/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 695us/step - accuracy: 0.8408 - loss: 0.45911246/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 696us/step - accuracy: 0.8411 - loss: 0.45861320/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 695us/step - accuracy: 0.8413 - loss: 0.45811321/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 695us/step - accuracy: 0.8413 - loss: 0.45801395/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 694us/step - accuracy: 0.8416 - loss: 0.45751396/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 695us/step - accuracy: 0.8416 - loss: 0.45741469/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 694us/step - accuracy: 0.8418 - loss: 0.45691470/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 694us/step - accuracy: 0.8418 - loss: 0.45691545/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 693us/step - accuracy: 0.8421 - loss: 0.45631546/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 693us/step - accuracy: 0.8421 - loss: 0.45631620/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 692us/step - accuracy: 0.8423 - loss: 0.45571621/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 692us/step - accuracy: 0.8423 - loss: 0.45571693/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 693us/step - accuracy: 0.8425 - loss: 0.45521694/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 693us/step - accuracy: 0.8425 - loss: 0.45521719/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 732us/step - accuracy: 0.8426 - loss: 0.4550 - val_accuracy: 0.8468 - val_loss: 0.4296
Epoch 4/30
   1/1719 ━━━━━━━━━━━━━━━━━━━━ 18s 11ms/step - accuracy: 0.8750 - loss: 0.4341  76/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 672us/step - accuracy: 0.8652 - loss: 0.4038 151/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 671us/step - accuracy: 0.8574 - loss: 0.4212 152/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 671us/step - accuracy: 0.8573 - loss: 0.4214 227/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 673us/step - accuracy: 0.8535 - loss: 0.4265 301/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 675us/step - accuracy: 0.8519 - loss: 0.4283 302/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 676us/step - accuracy: 0.8519 - loss: 0.4283 378/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 673us/step - accuracy: 0.8511 - loss: 0.4291 452/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 674us/step - accuracy: 0.8505 - loss: 0.4297 453/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 675us/step - accuracy: 0.8505 - loss: 0.4297 528/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 674us/step - accuracy: 0.8503 - loss: 0.4300 529/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 674us/step - accuracy: 0.8503 - loss: 0.4300 602/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 676us/step - accuracy: 0.8503 - loss: 0.4299 603/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 676us/step - accuracy: 0.8503 - loss: 0.4299 674/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 680us/step - accuracy: 0.8504 - loss: 0.4297 749/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 679us/step - accuracy: 0.8505 - loss: 0.4296 750/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 679us/step - accuracy: 0.8505 - loss: 0.4295 823/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 680us/step - accuracy: 0.8507 - loss: 0.4293 897/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 680us/step - accuracy: 0.8509 - loss: 0.4292 898/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 680us/step - accuracy: 0.8509 - loss: 0.4292 971/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 681us/step - accuracy: 0.8511 - loss: 0.42881045/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 681us/step - accuracy: 0.8512 - loss: 0.42831120/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 680us/step - accuracy: 0.8514 - loss: 0.42781192/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 681us/step - accuracy: 0.8516 - loss: 0.42731193/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 681us/step - accuracy: 0.8516 - loss: 0.42731266/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 682us/step - accuracy: 0.8517 - loss: 0.42691267/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 682us/step - accuracy: 0.8517 - loss: 0.42691339/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 683us/step - accuracy: 0.8519 - loss: 0.42651340/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 683us/step - accuracy: 0.8519 - loss: 0.42651414/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 683us/step - accuracy: 0.8520 - loss: 0.42601415/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 683us/step - accuracy: 0.8520 - loss: 0.42601489/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 683us/step - accuracy: 0.8522 - loss: 0.42561490/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 683us/step - accuracy: 0.8522 - loss: 0.42561561/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 684us/step - accuracy: 0.8523 - loss: 0.42521632/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 685us/step - accuracy: 0.8524 - loss: 0.42481633/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 685us/step - accuracy: 0.8524 - loss: 0.42481705/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 686us/step - accuracy: 0.8525 - loss: 0.42441706/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 686us/step - accuracy: 0.8525 - loss: 0.42441719/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 728us/step - accuracy: 0.8526 - loss: 0.4243 - val_accuracy: 0.8498 - val_loss: 0.4154
Epoch 5/30
   1/1719 ━━━━━━━━━━━━━━━━━━━━ 18s 11ms/step - accuracy: 0.8750 - loss: 0.4185  71/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 717us/step - accuracy: 0.8688 - loss: 0.3787  72/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 719us/step - accuracy: 0.8688 - loss: 0.3788 146/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 701us/step - accuracy: 0.8631 - loss: 0.3960 147/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 701us/step - accuracy: 0.8630 - loss: 0.3961 218/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 705us/step - accuracy: 0.8603 - loss: 0.4022 219/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 706us/step - accuracy: 0.8603 - loss: 0.4022 292/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 702us/step - accuracy: 0.8592 - loss: 0.4043 367/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 696us/step - accuracy: 0.8587 - loss: 0.4054 368/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 697us/step - accuracy: 0.8587 - loss: 0.4054 442/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 694us/step - accuracy: 0.8585 - loss: 0.4062 443/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 694us/step - accuracy: 0.8585 - loss: 0.4062 516/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 694us/step - accuracy: 0.8583 - loss: 0.4066 517/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 694us/step - accuracy: 0.8583 - loss: 0.4066 592/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 692us/step - accuracy: 0.8584 - loss: 0.4067 667/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 690us/step - accuracy: 0.8585 - loss: 0.4066 742/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 688us/step - accuracy: 0.8587 - loss: 0.4065 743/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 688us/step - accuracy: 0.8587 - loss: 0.4065 818/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 686us/step - accuracy: 0.8588 - loss: 0.4064 893/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 685us/step - accuracy: 0.8590 - loss: 0.4063 894/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 685us/step - accuracy: 0.8590 - loss: 0.4063 965/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 687us/step - accuracy: 0.8591 - loss: 0.4060 966/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 687us/step - accuracy: 0.8591 - loss: 0.40601039/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 687us/step - accuracy: 0.8593 - loss: 0.40571040/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 687us/step - accuracy: 0.8593 - loss: 0.40571114/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 686us/step - accuracy: 0.8595 - loss: 0.40521115/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 687us/step - accuracy: 0.8595 - loss: 0.40521188/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 687us/step - accuracy: 0.8596 - loss: 0.40481262/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 686us/step - accuracy: 0.8597 - loss: 0.40451263/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 686us/step - accuracy: 0.8597 - loss: 0.40451337/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 686us/step - accuracy: 0.8598 - loss: 0.40421338/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 686us/step - accuracy: 0.8598 - loss: 0.40421411/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 686us/step - accuracy: 0.8600 - loss: 0.40381412/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 686us/step - accuracy: 0.8600 - loss: 0.40381488/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 685us/step - accuracy: 0.8601 - loss: 0.40341489/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 685us/step - accuracy: 0.8601 - loss: 0.40341564/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 685us/step - accuracy: 0.8602 - loss: 0.40301638/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 685us/step - accuracy: 0.8603 - loss: 0.40271639/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 685us/step - accuracy: 0.8603 - loss: 0.40271712/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 685us/step - accuracy: 0.8604 - loss: 0.40241713/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 685us/step - accuracy: 0.8604 - loss: 0.40241719/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 724us/step - accuracy: 0.8604 - loss: 0.4024 - val_accuracy: 0.8552 - val_loss: 0.4039
Epoch 6/30
   1/1719 ━━━━━━━━━━━━━━━━━━━━ 17s 10ms/step - accuracy: 0.8438 - loss: 0.3977  75/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 680us/step - accuracy: 0.8718 - loss: 0.3592  76/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 682us/step - accuracy: 0.8718 - loss: 0.3594 151/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 676us/step - accuracy: 0.8682 - loss: 0.3768 152/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 676us/step - accuracy: 0.8681 - loss: 0.3770 227/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 675us/step - accuracy: 0.8662 - loss: 0.3831 228/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 676us/step - accuracy: 0.8662 - loss: 0.3831 302/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 676us/step - accuracy: 0.8655 - loss: 0.3854 303/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 676us/step - accuracy: 0.8655 - loss: 0.3854 378/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 675us/step - accuracy: 0.8652 - loss: 0.3867 379/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 675us/step - accuracy: 0.8652 - loss: 0.3867 455/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 674us/step - accuracy: 0.8650 - loss: 0.3876 532/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 671us/step - accuracy: 0.8648 - loss: 0.3881 533/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 671us/step - accuracy: 0.8648 - loss: 0.3881 605/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 674us/step - accuracy: 0.8647 - loss: 0.3882 606/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 674us/step - accuracy: 0.8647 - loss: 0.3882 679/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 676us/step - accuracy: 0.8648 - loss: 0.3881 680/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 676us/step - accuracy: 0.8648 - loss: 0.3881 755/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 676us/step - accuracy: 0.8648 - loss: 0.3881 756/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 676us/step - accuracy: 0.8648 - loss: 0.3881 831/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 676us/step - accuracy: 0.8649 - loss: 0.3880 832/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 676us/step - accuracy: 0.8649 - loss: 0.3880 907/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 676us/step - accuracy: 0.8649 - loss: 0.3881 908/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 676us/step - accuracy: 0.8649 - loss: 0.3881 983/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 676us/step - accuracy: 0.8650 - loss: 0.3879 984/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 676us/step - accuracy: 0.8650 - loss: 0.38781057/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 676us/step - accuracy: 0.8651 - loss: 0.38751132/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 676us/step - accuracy: 0.8652 - loss: 0.38721133/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 676us/step - accuracy: 0.8652 - loss: 0.38721206/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 677us/step - accuracy: 0.8653 - loss: 0.38681207/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 677us/step - accuracy: 0.8653 - loss: 0.38681278/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 679us/step - accuracy: 0.8654 - loss: 0.38661279/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 679us/step - accuracy: 0.8654 - loss: 0.38661351/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 680us/step - accuracy: 0.8654 - loss: 0.38631352/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 680us/step - accuracy: 0.8654 - loss: 0.38631423/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 681us/step - accuracy: 0.8655 - loss: 0.38601496/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 682us/step - accuracy: 0.8656 - loss: 0.38571497/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 682us/step - accuracy: 0.8656 - loss: 0.38571572/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 682us/step - accuracy: 0.8657 - loss: 0.38541647/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 681us/step - accuracy: 0.8657 - loss: 0.38511719/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 682us/step - accuracy: 0.8658 - loss: 0.38491719/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 723us/step - accuracy: 0.8658 - loss: 0.3849 - val_accuracy: 0.8562 - val_loss: 0.3939
Epoch 7/30
   1/1719 ━━━━━━━━━━━━━━━━━━━━ 18s 11ms/step - accuracy: 0.8438 - loss: 0.3789  75/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 681us/step - accuracy: 0.8755 - loss: 0.3426  76/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 684us/step - accuracy: 0.8755 - loss: 0.3428 148/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 690us/step - accuracy: 0.8723 - loss: 0.3598 149/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 692us/step - accuracy: 0.8723 - loss: 0.3600 220/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 697us/step - accuracy: 0.8706 - loss: 0.3667 292/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 699us/step - accuracy: 0.8700 - loss: 0.3692 293/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 699us/step - accuracy: 0.8700 - loss: 0.3692 366/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 698us/step - accuracy: 0.8697 - loss: 0.3707 441/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 693us/step - accuracy: 0.8694 - loss: 0.3718 515/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 691us/step - accuracy: 0.8692 - loss: 0.3724 516/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 692us/step - accuracy: 0.8692 - loss: 0.3724 588/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 692us/step - accuracy: 0.8692 - loss: 0.3728 589/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 693us/step - accuracy: 0.8692 - loss: 0.3728 662/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 692us/step - accuracy: 0.8692 - loss: 0.3727 663/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 692us/step - accuracy: 0.8692 - loss: 0.3727 737/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 690us/step - accuracy: 0.8693 - loss: 0.3727 738/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 690us/step - accuracy: 0.8693 - loss: 0.3728 812/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 690us/step - accuracy: 0.8694 - loss: 0.3728 813/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 690us/step - accuracy: 0.8694 - loss: 0.3728 885/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 691us/step - accuracy: 0.8694 - loss: 0.3729 886/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 691us/step - accuracy: 0.8694 - loss: 0.3729 959/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 691us/step - accuracy: 0.8694 - loss: 0.3728 960/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 691us/step - accuracy: 0.8694 - loss: 0.37281033/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 691us/step - accuracy: 0.8695 - loss: 0.37261034/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 691us/step - accuracy: 0.8695 - loss: 0.37261107/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 691us/step - accuracy: 0.8696 - loss: 0.37231181/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 690us/step - accuracy: 0.8697 - loss: 0.37201182/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 690us/step - accuracy: 0.8697 - loss: 0.37201255/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 690us/step - accuracy: 0.8698 - loss: 0.37181326/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 691us/step - accuracy: 0.8699 - loss: 0.37151327/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 691us/step - accuracy: 0.8699 - loss: 0.37151401/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 691us/step - accuracy: 0.8700 - loss: 0.37131402/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 691us/step - accuracy: 0.8700 - loss: 0.37131476/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 690us/step - accuracy: 0.8701 - loss: 0.37101551/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 689us/step - accuracy: 0.8702 - loss: 0.37071620/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 691us/step - accuracy: 0.8702 - loss: 0.37051621/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 691us/step - accuracy: 0.8702 - loss: 0.37051693/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 691us/step - accuracy: 0.8703 - loss: 0.37031694/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 691us/step - accuracy: 0.8703 - loss: 0.37031719/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 733us/step - accuracy: 0.8703 - loss: 0.3703 - val_accuracy: 0.8616 - val_loss: 0.3859
Epoch 8/30
   1/1719 ━━━━━━━━━━━━━━━━━━━━ 18s 11ms/step - accuracy: 0.8438 - loss: 0.3621  76/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 667us/step - accuracy: 0.8795 - loss: 0.3293  77/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 670us/step - accuracy: 0.8794 - loss: 0.3295 151/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 674us/step - accuracy: 0.8755 - loss: 0.3467 223/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 683us/step - accuracy: 0.8735 - loss: 0.3533 224/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 684us/step - accuracy: 0.8735 - loss: 0.3534 291/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 700us/step - accuracy: 0.8728 - loss: 0.3558 292/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 701us/step - accuracy: 0.8728 - loss: 0.3558 359/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 711us/step - accuracy: 0.8725 - loss: 0.3573 430/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 711us/step - accuracy: 0.8722 - loss: 0.3585 431/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 712us/step - accuracy: 0.8722 - loss: 0.3585 500/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 714us/step - accuracy: 0.8720 - loss: 0.3592 501/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 714us/step - accuracy: 0.8720 - loss: 0.3592 573/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 712us/step - accuracy: 0.8720 - loss: 0.3597 574/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 712us/step - accuracy: 0.8720 - loss: 0.3597 647/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 710us/step - accuracy: 0.8721 - loss: 0.3597 648/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 710us/step - accuracy: 0.8721 - loss: 0.3597 723/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 706us/step - accuracy: 0.8722 - loss: 0.3598 724/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 706us/step - accuracy: 0.8722 - loss: 0.3598 796/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 705us/step - accuracy: 0.8722 - loss: 0.3599 797/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 706us/step - accuracy: 0.8722 - loss: 0.3599 872/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 703us/step - accuracy: 0.8723 - loss: 0.3600 873/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 703us/step - accuracy: 0.8723 - loss: 0.3600 945/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 702us/step - accuracy: 0.8723 - loss: 0.36001020/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 700us/step - accuracy: 0.8724 - loss: 0.35991021/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 700us/step - accuracy: 0.8724 - loss: 0.35991095/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 699us/step - accuracy: 0.8726 - loss: 0.35971169/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 698us/step - accuracy: 0.8727 - loss: 0.35941170/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 698us/step - accuracy: 0.8727 - loss: 0.35941241/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 699us/step - accuracy: 0.8728 - loss: 0.35921242/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 699us/step - accuracy: 0.8728 - loss: 0.35921315/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 698us/step - accuracy: 0.8729 - loss: 0.35901388/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 698us/step - accuracy: 0.8730 - loss: 0.35881389/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 698us/step - accuracy: 0.8730 - loss: 0.35881465/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 696us/step - accuracy: 0.8731 - loss: 0.35851466/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 696us/step - accuracy: 0.8731 - loss: 0.35851539/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 696us/step - accuracy: 0.8732 - loss: 0.35831540/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 696us/step - accuracy: 0.8732 - loss: 0.35831612/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 696us/step - accuracy: 0.8733 - loss: 0.35811678/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 699us/step - accuracy: 0.8734 - loss: 0.35801679/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 699us/step - accuracy: 0.8734 - loss: 0.35801719/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 745us/step - accuracy: 0.8734 - loss: 0.3579 - val_accuracy: 0.8632 - val_loss: 0.3794
Epoch 9/30
   1/1719 ━━━━━━━━━━━━━━━━━━━━ 20s 12ms/step - accuracy: 0.8750 - loss: 0.3380   2/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 868us/step - accuracy: 0.8828 - loss: 0.3159  73/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 712us/step - accuracy: 0.8833 - loss: 0.3163  74/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 715us/step - accuracy: 0.8832 - loss: 0.3164 148/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 698us/step - accuracy: 0.8790 - loss: 0.3339 149/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 700us/step - accuracy: 0.8789 - loss: 0.3341 223/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 693us/step - accuracy: 0.8769 - loss: 0.3413 224/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 693us/step - accuracy: 0.8769 - loss: 0.3414 297/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 692us/step - accuracy: 0.8764 - loss: 0.3442 298/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 693us/step - accuracy: 0.8764 - loss: 0.3442 371/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 692us/step - accuracy: 0.8761 - loss: 0.3458 372/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 692us/step - accuracy: 0.8761 - loss: 0.3458 446/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 690us/step - accuracy: 0.8759 - loss: 0.3471 447/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 690us/step - accuracy: 0.8759 - loss: 0.3471 520/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 690us/step - accuracy: 0.8757 - loss: 0.3478 595/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 687us/step - accuracy: 0.8756 - loss: 0.3482 672/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 684us/step - accuracy: 0.8758 - loss: 0.3483 673/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 684us/step - accuracy: 0.8758 - loss: 0.3483 747/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 684us/step - accuracy: 0.8759 - loss: 0.3484 748/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 684us/step - accuracy: 0.8759 - loss: 0.3484 820/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 685us/step - accuracy: 0.8759 - loss: 0.3485 821/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 686us/step - accuracy: 0.8759 - loss: 0.3485 893/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 686us/step - accuracy: 0.8759 - loss: 0.3487 894/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 687us/step - accuracy: 0.8759 - loss: 0.3487 968/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 687us/step - accuracy: 0.8760 - loss: 0.34871043/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 685us/step - accuracy: 0.8761 - loss: 0.34851118/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 685us/step - accuracy: 0.8763 - loss: 0.34831119/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 685us/step - accuracy: 0.8763 - loss: 0.34831194/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 684us/step - accuracy: 0.8764 - loss: 0.34811195/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 684us/step - accuracy: 0.8764 - loss: 0.34811270/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 684us/step - accuracy: 0.8765 - loss: 0.34791271/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 684us/step - accuracy: 0.8765 - loss: 0.34791346/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 683us/step - accuracy: 0.8766 - loss: 0.34771420/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 683us/step - accuracy: 0.8767 - loss: 0.34751495/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 682us/step - accuracy: 0.8768 - loss: 0.34731496/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 682us/step - accuracy: 0.8768 - loss: 0.34731569/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 682us/step - accuracy: 0.8769 - loss: 0.34711642/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 683us/step - accuracy: 0.8770 - loss: 0.34701716/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 683us/step - accuracy: 0.8770 - loss: 0.34681719/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 722us/step - accuracy: 0.8770 - loss: 0.3468 - val_accuracy: 0.8636 - val_loss: 0.3739
Epoch 10/30
   1/1719 ━━━━━━━━━━━━━━━━━━━━ 17s 10ms/step - accuracy: 0.9062 - loss: 0.3244  76/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 668us/step - accuracy: 0.8869 - loss: 0.3066  77/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 669us/step - accuracy: 0.8868 - loss: 0.3068 152/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 671us/step - accuracy: 0.8822 - loss: 0.3240 153/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 672us/step - accuracy: 0.8821 - loss: 0.3242 228/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 672us/step - accuracy: 0.8801 - loss: 0.3310 304/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 670us/step - accuracy: 0.8795 - loss: 0.3339 305/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 671us/step - accuracy: 0.8795 - loss: 0.3339 381/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 670us/step - accuracy: 0.8792 - loss: 0.3356 452/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 676us/step - accuracy: 0.8789 - loss: 0.3368 453/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 677us/step - accuracy: 0.8789 - loss: 0.3368 526/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 679us/step - accuracy: 0.8787 - loss: 0.3376 527/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 679us/step - accuracy: 0.8787 - loss: 0.3376 600/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 681us/step - accuracy: 0.8786 - loss: 0.3380 601/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 681us/step - accuracy: 0.8786 - loss: 0.3380 674/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 682us/step - accuracy: 0.8787 - loss: 0.3380 748/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 682us/step - accuracy: 0.8787 - loss: 0.3382 749/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 682us/step - accuracy: 0.8787 - loss: 0.3382 823/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 682us/step - accuracy: 0.8788 - loss: 0.3383 824/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 682us/step - accuracy: 0.8788 - loss: 0.3383 898/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 682us/step - accuracy: 0.8788 - loss: 0.3386 899/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 682us/step - accuracy: 0.8788 - loss: 0.3386 973/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 682us/step - accuracy: 0.8788 - loss: 0.33861049/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 681us/step - accuracy: 0.8789 - loss: 0.33841121/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 682us/step - accuracy: 0.8790 - loss: 0.33831192/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 683us/step - accuracy: 0.8792 - loss: 0.33811193/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 683us/step - accuracy: 0.8792 - loss: 0.33811261/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 687us/step - accuracy: 0.8792 - loss: 0.33801327/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 691us/step - accuracy: 0.8793 - loss: 0.33781328/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 691us/step - accuracy: 0.8793 - loss: 0.33781399/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 692us/step - accuracy: 0.8794 - loss: 0.33761400/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 692us/step - accuracy: 0.8794 - loss: 0.33761467/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 695us/step - accuracy: 0.8795 - loss: 0.33751536/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 696us/step - accuracy: 0.8796 - loss: 0.33731537/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 697us/step - accuracy: 0.8796 - loss: 0.33731604/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 699us/step - accuracy: 0.8797 - loss: 0.33721605/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 699us/step - accuracy: 0.8797 - loss: 0.33721673/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 701us/step - accuracy: 0.8797 - loss: 0.33711674/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 701us/step - accuracy: 0.8797 - loss: 0.33711719/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 747us/step - accuracy: 0.8798 - loss: 0.3370 - val_accuracy: 0.8676 - val_loss: 0.3684
Epoch 11/30
   1/1719 ━━━━━━━━━━━━━━━━━━━━ 21s 13ms/step - accuracy: 0.9062 - loss: 0.3119   2/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 1ms/step - accuracy: 0.9062 - loss: 0.2937    68/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 766us/step - accuracy: 0.8884 - loss: 0.2958 138/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 740us/step - accuracy: 0.8842 - loss: 0.3119 139/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 743us/step - accuracy: 0.8841 - loss: 0.3121 207/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 741us/step - accuracy: 0.8820 - loss: 0.3203 208/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 742us/step - accuracy: 0.8819 - loss: 0.3204 277/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 740us/step - accuracy: 0.8815 - loss: 0.3236 278/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 741us/step - accuracy: 0.8815 - loss: 0.3237 347/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 738us/step - accuracy: 0.8813 - loss: 0.3255 348/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 738us/step - accuracy: 0.8813 - loss: 0.3256 417/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 738us/step - accuracy: 0.8810 - loss: 0.3271 418/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 738us/step - accuracy: 0.8810 - loss: 0.3271 486/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 738us/step - accuracy: 0.8810 - loss: 0.3280 487/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 739us/step - accuracy: 0.8810 - loss: 0.3280 553/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 742us/step - accuracy: 0.8808 - loss: 0.3286 554/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 742us/step - accuracy: 0.8808 - loss: 0.3286 621/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 743us/step - accuracy: 0.8809 - loss: 0.3288 622/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 743us/step - accuracy: 0.8809 - loss: 0.3288 689/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 743us/step - accuracy: 0.8810 - loss: 0.3289 690/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 743us/step - accuracy: 0.8810 - loss: 0.3289 756/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 745us/step - accuracy: 0.8810 - loss: 0.3290 757/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 745us/step - accuracy: 0.8810 - loss: 0.3290 824/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 745us/step - accuracy: 0.8810 - loss: 0.3292 825/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 746us/step - accuracy: 0.8810 - loss: 0.3292 893/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 745us/step - accuracy: 0.8810 - loss: 0.3294 894/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 745us/step - accuracy: 0.8810 - loss: 0.3294 963/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 744us/step - accuracy: 0.8811 - loss: 0.3295 964/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 744us/step - accuracy: 0.8811 - loss: 0.32951033/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 744us/step - accuracy: 0.8812 - loss: 0.32941034/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 744us/step - accuracy: 0.8812 - loss: 0.32941103/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 743us/step - accuracy: 0.8813 - loss: 0.32921104/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 743us/step - accuracy: 0.8813 - loss: 0.32921172/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 743us/step - accuracy: 0.8814 - loss: 0.32911173/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 743us/step - accuracy: 0.8814 - loss: 0.32911240/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 743us/step - accuracy: 0.8815 - loss: 0.32901241/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 743us/step - accuracy: 0.8815 - loss: 0.32901313/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 741us/step - accuracy: 0.8816 - loss: 0.32881314/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 741us/step - accuracy: 0.8816 - loss: 0.32881383/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 741us/step - accuracy: 0.8817 - loss: 0.32871452/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 740us/step - accuracy: 0.8818 - loss: 0.32851453/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 740us/step - accuracy: 0.8818 - loss: 0.32851520/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 741us/step - accuracy: 0.8819 - loss: 0.32841521/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 741us/step - accuracy: 0.8819 - loss: 0.32841589/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 741us/step - accuracy: 0.8820 - loss: 0.32831590/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 741us/step - accuracy: 0.8820 - loss: 0.32821659/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 741us/step - accuracy: 0.8820 - loss: 0.32811660/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 741us/step - accuracy: 0.8820 - loss: 0.32811719/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 786us/step - accuracy: 0.8821 - loss: 0.3280 - val_accuracy: 0.8672 - val_loss: 0.3647
Epoch 12/30
   1/1719 ━━━━━━━━━━━━━━━━━━━━ 20s 12ms/step - accuracy: 0.9062 - loss: 0.3033   2/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 947us/step - accuracy: 0.9062 - loss: 0.2855  73/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 712us/step - accuracy: 0.8900 - loss: 0.2882  74/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 715us/step - accuracy: 0.8900 - loss: 0.2884 145/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 712us/step - accuracy: 0.8858 - loss: 0.3047 216/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 712us/step - accuracy: 0.8841 - loss: 0.3124 217/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 712us/step - accuracy: 0.8841 - loss: 0.3125 286/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 716us/step - accuracy: 0.8839 - loss: 0.3155 354/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 722us/step - accuracy: 0.8838 - loss: 0.3172 355/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 723us/step - accuracy: 0.8838 - loss: 0.3172 423/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 726us/step - accuracy: 0.8837 - loss: 0.3187 424/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 726us/step - accuracy: 0.8837 - loss: 0.3187 493/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 727us/step - accuracy: 0.8836 - loss: 0.3195 494/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 727us/step - accuracy: 0.8836 - loss: 0.3196 564/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 727us/step - accuracy: 0.8836 - loss: 0.3201 565/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 727us/step - accuracy: 0.8836 - loss: 0.3201 633/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 729us/step - accuracy: 0.8836 - loss: 0.3203 634/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 729us/step - accuracy: 0.8836 - loss: 0.3203 703/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 730us/step - accuracy: 0.8837 - loss: 0.3204 704/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 730us/step - accuracy: 0.8837 - loss: 0.3204 773/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 730us/step - accuracy: 0.8838 - loss: 0.3206 774/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 731us/step - accuracy: 0.8838 - loss: 0.3206 842/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 732us/step - accuracy: 0.8838 - loss: 0.3208 843/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 732us/step - accuracy: 0.8838 - loss: 0.3208 911/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 733us/step - accuracy: 0.8838 - loss: 0.3210 912/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 733us/step - accuracy: 0.8838 - loss: 0.3210 982/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 732us/step - accuracy: 0.8839 - loss: 0.3210 983/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 732us/step - accuracy: 0.8839 - loss: 0.32101054/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 731us/step - accuracy: 0.8839 - loss: 0.32101055/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 731us/step - accuracy: 0.8839 - loss: 0.32101127/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 729us/step - accuracy: 0.8841 - loss: 0.32081128/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 729us/step - accuracy: 0.8841 - loss: 0.32081201/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 727us/step - accuracy: 0.8842 - loss: 0.32071202/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 727us/step - accuracy: 0.8842 - loss: 0.32071271/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 727us/step - accuracy: 0.8843 - loss: 0.32061272/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 727us/step - accuracy: 0.8843 - loss: 0.32061345/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 725us/step - accuracy: 0.8844 - loss: 0.32041346/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 725us/step - accuracy: 0.8844 - loss: 0.32041420/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 723us/step - accuracy: 0.8845 - loss: 0.32031421/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 723us/step - accuracy: 0.8845 - loss: 0.32031495/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 721us/step - accuracy: 0.8846 - loss: 0.32011496/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 721us/step - accuracy: 0.8846 - loss: 0.32011570/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 719us/step - accuracy: 0.8847 - loss: 0.32001571/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 719us/step - accuracy: 0.8847 - loss: 0.32001643/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 718us/step - accuracy: 0.8848 - loss: 0.31991644/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 718us/step - accuracy: 0.8848 - loss: 0.31991717/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 717us/step - accuracy: 0.8848 - loss: 0.31981719/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 761us/step - accuracy: 0.8848 - loss: 0.3198 - val_accuracy: 0.8688 - val_loss: 0.3618
Epoch 13/30
   1/1719 ━━━━━━━━━━━━━━━━━━━━ 19s 12ms/step - accuracy: 0.9062 - loss: 0.2949  69/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 740us/step - accuracy: 0.8912 - loss: 0.2804  70/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 743us/step - accuracy: 0.8912 - loss: 0.2805 143/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 714us/step - accuracy: 0.8874 - loss: 0.2967 144/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 715us/step - accuracy: 0.8874 - loss: 0.2969 216/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 710us/step - accuracy: 0.8860 - loss: 0.3047 289/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 706us/step - accuracy: 0.8861 - loss: 0.3078 361/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 704us/step - accuracy: 0.8862 - loss: 0.3096 362/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 704us/step - accuracy: 0.8862 - loss: 0.3096 434/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 704us/step - accuracy: 0.8862 - loss: 0.3110 435/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 704us/step - accuracy: 0.8862 - loss: 0.3110 508/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 703us/step - accuracy: 0.8863 - loss: 0.3118 509/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 703us/step - accuracy: 0.8863 - loss: 0.3119 580/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 704us/step - accuracy: 0.8863 - loss: 0.3124 652/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 704us/step - accuracy: 0.8864 - loss: 0.3125 720/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 707us/step - accuracy: 0.8865 - loss: 0.3126 721/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 708us/step - accuracy: 0.8865 - loss: 0.3126 790/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 710us/step - accuracy: 0.8865 - loss: 0.3128 791/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 710us/step - accuracy: 0.8865 - loss: 0.3128 860/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 712us/step - accuracy: 0.8865 - loss: 0.3130 861/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 712us/step - accuracy: 0.8865 - loss: 0.3130 929/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 715us/step - accuracy: 0.8866 - loss: 0.3132 930/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 715us/step - accuracy: 0.8866 - loss: 0.3132 998/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 717us/step - accuracy: 0.8866 - loss: 0.3132 999/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 717us/step - accuracy: 0.8866 - loss: 0.31321066/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 719us/step - accuracy: 0.8867 - loss: 0.31311067/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 720us/step - accuracy: 0.8867 - loss: 0.31311133/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 722us/step - accuracy: 0.8868 - loss: 0.31291134/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 722us/step - accuracy: 0.8868 - loss: 0.31291200/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 724us/step - accuracy: 0.8869 - loss: 0.31281201/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 724us/step - accuracy: 0.8869 - loss: 0.31281268/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 726us/step - accuracy: 0.8870 - loss: 0.31271269/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 726us/step - accuracy: 0.8870 - loss: 0.31271340/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 725us/step - accuracy: 0.8871 - loss: 0.31261341/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 725us/step - accuracy: 0.8871 - loss: 0.31261412/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 725us/step - accuracy: 0.8872 - loss: 0.31251413/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 725us/step - accuracy: 0.8872 - loss: 0.31251484/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 724us/step - accuracy: 0.8873 - loss: 0.31231557/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 722us/step - accuracy: 0.8874 - loss: 0.31221631/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 720us/step - accuracy: 0.8874 - loss: 0.31211632/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 720us/step - accuracy: 0.8874 - loss: 0.31211705/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 719us/step - accuracy: 0.8875 - loss: 0.31201706/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 719us/step - accuracy: 0.8875 - loss: 0.31201719/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 761us/step - accuracy: 0.8875 - loss: 0.3120 - val_accuracy: 0.8688 - val_loss: 0.3599
Epoch 14/30
   1/1719 ━━━━━━━━━━━━━━━━━━━━ 19s 11ms/step - accuracy: 0.9375 - loss: 0.2838  71/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 718us/step - accuracy: 0.8973 - loss: 0.2725  72/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 721us/step - accuracy: 0.8972 - loss: 0.2726 145/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 704us/step - accuracy: 0.8929 - loss: 0.2889 218/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 700us/step - accuracy: 0.8910 - loss: 0.2967 219/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 702us/step - accuracy: 0.8909 - loss: 0.2967 220/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 703us/step - accuracy: 0.8909 - loss: 0.2968 290/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 708us/step - accuracy: 0.8906 - loss: 0.2999 291/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 709us/step - accuracy: 0.8906 - loss: 0.2999 360/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 713us/step - accuracy: 0.8904 - loss: 0.3017 361/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 714us/step - accuracy: 0.8903 - loss: 0.3017 430/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 717us/step - accuracy: 0.8901 - loss: 0.3031 431/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 717us/step - accuracy: 0.8901 - loss: 0.3031 499/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 721us/step - accuracy: 0.8900 - loss: 0.3040 500/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 722us/step - accuracy: 0.8900 - loss: 0.3040 570/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 721us/step - accuracy: 0.8900 - loss: 0.3046 571/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 722us/step - accuracy: 0.8900 - loss: 0.3046 643/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 719us/step - accuracy: 0.8900 - loss: 0.3047 644/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 719us/step - accuracy: 0.8900 - loss: 0.3047 715/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 718us/step - accuracy: 0.8900 - loss: 0.3049 716/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 718us/step - accuracy: 0.8900 - loss: 0.3049 787/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 717us/step - accuracy: 0.8900 - loss: 0.3051 788/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 717us/step - accuracy: 0.8900 - loss: 0.3051 863/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 713us/step - accuracy: 0.8900 - loss: 0.3053 938/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 710us/step - accuracy: 0.8900 - loss: 0.3055 939/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 710us/step - accuracy: 0.8900 - loss: 0.30551013/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 708us/step - accuracy: 0.8900 - loss: 0.30551014/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 708us/step - accuracy: 0.8900 - loss: 0.30551088/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 706us/step - accuracy: 0.8900 - loss: 0.30541089/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 706us/step - accuracy: 0.8900 - loss: 0.30541163/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 705us/step - accuracy: 0.8901 - loss: 0.30531164/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 705us/step - accuracy: 0.8901 - loss: 0.30531237/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 704us/step - accuracy: 0.8902 - loss: 0.30521311/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 702us/step - accuracy: 0.8902 - loss: 0.30511312/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 702us/step - accuracy: 0.8902 - loss: 0.30511387/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 701us/step - accuracy: 0.8903 - loss: 0.30501388/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 701us/step - accuracy: 0.8903 - loss: 0.30501457/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 703us/step - accuracy: 0.8904 - loss: 0.30491458/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 703us/step - accuracy: 0.8904 - loss: 0.30491525/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 705us/step - accuracy: 0.8904 - loss: 0.30481526/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 705us/step - accuracy: 0.8904 - loss: 0.30481594/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 707us/step - accuracy: 0.8905 - loss: 0.30471595/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 707us/step - accuracy: 0.8905 - loss: 0.30471664/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 708us/step - accuracy: 0.8905 - loss: 0.30461665/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 708us/step - accuracy: 0.8905 - loss: 0.30461719/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 749us/step - accuracy: 0.8905 - loss: 0.3046 - val_accuracy: 0.8702 - val_loss: 0.3539
Epoch 15/30
   1/1719 ━━━━━━━━━━━━━━━━━━━━ 19s 11ms/step - accuracy: 0.9375 - loss: 0.2624  71/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 723us/step - accuracy: 0.9008 - loss: 0.2656 145/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 703us/step - accuracy: 0.8960 - loss: 0.2819 146/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 704us/step - accuracy: 0.8959 - loss: 0.2821 218/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 703us/step - accuracy: 0.8937 - loss: 0.2897 219/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 704us/step - accuracy: 0.8937 - loss: 0.2898 257/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 795us/step - accuracy: 0.8936 - loss: 0.2917 258/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 796us/step - accuracy: 0.8936 - loss: 0.2917 324/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 790us/step - accuracy: 0.8934 - loss: 0.2938 325/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 791us/step - accuracy: 0.8934 - loss: 0.2938 395/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 778us/step - accuracy: 0.8931 - loss: 0.2956 396/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 778us/step - accuracy: 0.8931 - loss: 0.2956 467/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 768us/step - accuracy: 0.8930 - loss: 0.2967 541/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 756us/step - accuracy: 0.8929 - loss: 0.2974 615/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 747us/step - accuracy: 0.8929 - loss: 0.2978 688/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 740us/step - accuracy: 0.8929 - loss: 0.2979 689/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 741us/step - accuracy: 0.8929 - loss: 0.2979 763/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 735us/step - accuracy: 0.8930 - loss: 0.2980 764/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 735us/step - accuracy: 0.8930 - loss: 0.2981 837/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 731us/step - accuracy: 0.8930 - loss: 0.2983 838/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 731us/step - accuracy: 0.8930 - loss: 0.2983 912/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 727us/step - accuracy: 0.8929 - loss: 0.2986 913/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 727us/step - accuracy: 0.8929 - loss: 0.2986 983/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 727us/step - accuracy: 0.8929 - loss: 0.2986 984/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 727us/step - accuracy: 0.8929 - loss: 0.29861055/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 725us/step - accuracy: 0.8930 - loss: 0.29861056/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 726us/step - accuracy: 0.8930 - loss: 0.29861127/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 724us/step - accuracy: 0.8931 - loss: 0.29851200/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 722us/step - accuracy: 0.8931 - loss: 0.29841201/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 722us/step - accuracy: 0.8931 - loss: 0.29841276/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 719us/step - accuracy: 0.8931 - loss: 0.29831348/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 718us/step - accuracy: 0.8932 - loss: 0.29821349/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 718us/step - accuracy: 0.8932 - loss: 0.29821421/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 717us/step - accuracy: 0.8933 - loss: 0.29811422/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 717us/step - accuracy: 0.8933 - loss: 0.29811495/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 716us/step - accuracy: 0.8933 - loss: 0.29801569/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 714us/step - accuracy: 0.8933 - loss: 0.29791570/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 714us/step - accuracy: 0.8933 - loss: 0.29791643/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 713us/step - accuracy: 0.8934 - loss: 0.29781644/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 713us/step - accuracy: 0.8934 - loss: 0.29781715/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 713us/step - accuracy: 0.8934 - loss: 0.29781716/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 714us/step - accuracy: 0.8934 - loss: 0.29781719/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 758us/step - accuracy: 0.8934 - loss: 0.2977 - val_accuracy: 0.8702 - val_loss: 0.3541
Epoch 16/30
   1/1719 ━━━━━━━━━━━━━━━━━━━━ 21s 13ms/step - accuracy: 0.9375 - loss: 0.2611  64/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 802us/step - accuracy: 0.9049 - loss: 0.2585  65/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 807us/step - accuracy: 0.9048 - loss: 0.2587 129/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 795us/step - accuracy: 0.8999 - loss: 0.2723 130/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 798us/step - accuracy: 0.8998 - loss: 0.2725 195/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 789us/step - accuracy: 0.8970 - loss: 0.2815 263/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 775us/step - accuracy: 0.8962 - loss: 0.2852 330/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 770us/step - accuracy: 0.8958 - loss: 0.2872 331/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 771us/step - accuracy: 0.8958 - loss: 0.2872 390/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 784us/step - accuracy: 0.8955 - loss: 0.2888 391/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 785us/step - accuracy: 0.8955 - loss: 0.2888 460/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 777us/step - accuracy: 0.8953 - loss: 0.2900 461/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 777us/step - accuracy: 0.8953 - loss: 0.2900 529/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 773us/step - accuracy: 0.8951 - loss: 0.2908 530/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 773us/step - accuracy: 0.8951 - loss: 0.2908 600/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 767us/step - accuracy: 0.8950 - loss: 0.2912 601/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 768us/step - accuracy: 0.8950 - loss: 0.2912 671/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 763us/step - accuracy: 0.8950 - loss: 0.2913 672/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 763us/step - accuracy: 0.8950 - loss: 0.2913 743/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 758us/step - accuracy: 0.8950 - loss: 0.2914 744/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 758us/step - accuracy: 0.8950 - loss: 0.2914 814/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 755us/step - accuracy: 0.8950 - loss: 0.2916 815/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 755us/step - accuracy: 0.8950 - loss: 0.2916 886/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 752us/step - accuracy: 0.8950 - loss: 0.2919 887/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 752us/step - accuracy: 0.8950 - loss: 0.2919 956/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 751us/step - accuracy: 0.8950 - loss: 0.2920 957/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 751us/step - accuracy: 0.8950 - loss: 0.29201026/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 749us/step - accuracy: 0.8950 - loss: 0.29201085/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 755us/step - accuracy: 0.8950 - loss: 0.29201086/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 756us/step - accuracy: 0.8950 - loss: 0.29201155/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 754us/step - accuracy: 0.8951 - loss: 0.29191156/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 754us/step - accuracy: 0.8951 - loss: 0.29191228/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 751us/step - accuracy: 0.8951 - loss: 0.29181229/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 751us/step - accuracy: 0.8951 - loss: 0.29181304/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 746us/step - accuracy: 0.8952 - loss: 0.29171305/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 747us/step - accuracy: 0.8952 - loss: 0.29171377/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 744us/step - accuracy: 0.8953 - loss: 0.29161378/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 744us/step - accuracy: 0.8953 - loss: 0.29161451/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 741us/step - accuracy: 0.8953 - loss: 0.29151525/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 739us/step - accuracy: 0.8954 - loss: 0.29141598/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 736us/step - accuracy: 0.8954 - loss: 0.29141673/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 733us/step - accuracy: 0.8955 - loss: 0.29131674/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 733us/step - accuracy: 0.8955 - loss: 0.29131719/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 771us/step - accuracy: 0.8955 - loss: 0.2913 - val_accuracy: 0.8724 - val_loss: 0.3508
Epoch 17/30
   1/1719 ━━━━━━━━━━━━━━━━━━━━ 18s 11ms/step - accuracy: 0.9375 - loss: 0.2457  70/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 727us/step - accuracy: 0.9057 - loss: 0.2530  71/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 731us/step - accuracy: 0.9056 - loss: 0.2531 143/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 716us/step - accuracy: 0.9003 - loss: 0.2685 216/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 707us/step - accuracy: 0.8979 - loss: 0.2765 289/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 702us/step - accuracy: 0.8974 - loss: 0.2799 290/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 703us/step - accuracy: 0.8974 - loss: 0.2799 364/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 698us/step - accuracy: 0.8971 - loss: 0.2818 365/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 698us/step - accuracy: 0.8971 - loss: 0.2819 438/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 697us/step - accuracy: 0.8968 - loss: 0.2834 439/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 697us/step - accuracy: 0.8968 - loss: 0.2834 511/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 698us/step - accuracy: 0.8968 - loss: 0.2843 512/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 698us/step - accuracy: 0.8968 - loss: 0.2843 585/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 697us/step - accuracy: 0.8968 - loss: 0.2848 659/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 696us/step - accuracy: 0.8968 - loss: 0.2850 660/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 696us/step - accuracy: 0.8968 - loss: 0.2850 732/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 696us/step - accuracy: 0.8969 - loss: 0.2851 733/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 696us/step - accuracy: 0.8969 - loss: 0.2852 800/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 700us/step - accuracy: 0.8969 - loss: 0.2854 801/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 701us/step - accuracy: 0.8969 - loss: 0.2854 872/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 702us/step - accuracy: 0.8969 - loss: 0.2857 873/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 702us/step - accuracy: 0.8969 - loss: 0.2857 946/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 701us/step - accuracy: 0.8969 - loss: 0.2858 947/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 701us/step - accuracy: 0.8969 - loss: 0.28581020/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 700us/step - accuracy: 0.8969 - loss: 0.28591021/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 700us/step - accuracy: 0.8969 - loss: 0.28591094/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 699us/step - accuracy: 0.8970 - loss: 0.28581095/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 699us/step - accuracy: 0.8970 - loss: 0.28581169/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 698us/step - accuracy: 0.8970 - loss: 0.28571243/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 697us/step - accuracy: 0.8971 - loss: 0.28571316/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 697us/step - accuracy: 0.8971 - loss: 0.28561317/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 697us/step - accuracy: 0.8971 - loss: 0.28561389/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 697us/step - accuracy: 0.8972 - loss: 0.28551461/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 697us/step - accuracy: 0.8973 - loss: 0.28541462/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 697us/step - accuracy: 0.8973 - loss: 0.28541532/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 698us/step - accuracy: 0.8973 - loss: 0.28541533/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 698us/step - accuracy: 0.8973 - loss: 0.28541604/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 698us/step - accuracy: 0.8974 - loss: 0.28531605/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 699us/step - accuracy: 0.8974 - loss: 0.28531678/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 698us/step - accuracy: 0.8974 - loss: 0.28521679/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 698us/step - accuracy: 0.8974 - loss: 0.28521719/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 739us/step - accuracy: 0.8974 - loss: 0.2852 - val_accuracy: 0.8718 - val_loss: 0.3503
Epoch 18/30
   1/1719 ━━━━━━━━━━━━━━━━━━━━ 19s 11ms/step - accuracy: 0.9375 - loss: 0.2378  72/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 711us/step - accuracy: 0.9090 - loss: 0.2476  73/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 713us/step - accuracy: 0.9089 - loss: 0.2477 146/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 700us/step - accuracy: 0.9026 - loss: 0.2631 147/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 701us/step - accuracy: 0.9026 - loss: 0.2633 220/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 697us/step - accuracy: 0.9002 - loss: 0.2707 221/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 698us/step - accuracy: 0.9002 - loss: 0.2708 293/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 698us/step - accuracy: 0.8997 - loss: 0.2739 294/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 698us/step - accuracy: 0.8997 - loss: 0.2740 366/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 699us/step - accuracy: 0.8994 - loss: 0.2758 367/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 699us/step - accuracy: 0.8994 - loss: 0.2759 438/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 701us/step - accuracy: 0.8990 - loss: 0.2774 439/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 701us/step - accuracy: 0.8990 - loss: 0.2774 511/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 702us/step - accuracy: 0.8989 - loss: 0.2783 585/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 698us/step - accuracy: 0.8989 - loss: 0.2788 659/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 696us/step - accuracy: 0.8989 - loss: 0.2790 660/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 696us/step - accuracy: 0.8989 - loss: 0.2790 733/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 696us/step - accuracy: 0.8989 - loss: 0.2792 808/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 694us/step - accuracy: 0.8990 - loss: 0.2794 809/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 694us/step - accuracy: 0.8990 - loss: 0.2794 881/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 694us/step - accuracy: 0.8989 - loss: 0.2797 882/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 694us/step - accuracy: 0.8989 - loss: 0.2797 954/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 695us/step - accuracy: 0.8989 - loss: 0.27991028/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 694us/step - accuracy: 0.8989 - loss: 0.27991099/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 695us/step - accuracy: 0.8990 - loss: 0.27991170/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 697us/step - accuracy: 0.8990 - loss: 0.27981171/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 697us/step - accuracy: 0.8990 - loss: 0.27981243/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 697us/step - accuracy: 0.8991 - loss: 0.27981244/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 697us/step - accuracy: 0.8991 - loss: 0.27981316/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 697us/step - accuracy: 0.8991 - loss: 0.27971317/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 697us/step - accuracy: 0.8991 - loss: 0.27971390/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 696us/step - accuracy: 0.8992 - loss: 0.27961391/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 696us/step - accuracy: 0.8992 - loss: 0.27961464/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 696us/step - accuracy: 0.8992 - loss: 0.27961538/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 696us/step - accuracy: 0.8993 - loss: 0.27951539/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 696us/step - accuracy: 0.8993 - loss: 0.27951611/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 696us/step - accuracy: 0.8993 - loss: 0.27941612/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 696us/step - accuracy: 0.8993 - loss: 0.27941682/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 697us/step - accuracy: 0.8994 - loss: 0.27941683/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 697us/step - accuracy: 0.8994 - loss: 0.27941719/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 741us/step - accuracy: 0.8994 - loss: 0.2794 - val_accuracy: 0.8732 - val_loss: 0.3496
Epoch 19/30
   1/1719 ━━━━━━━━━━━━━━━━━━━━ 19s 11ms/step - accuracy: 0.9375 - loss: 0.2318  71/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 718us/step - accuracy: 0.9124 - loss: 0.2421  72/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 721us/step - accuracy: 0.9123 - loss: 0.2422 146/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 701us/step - accuracy: 0.9056 - loss: 0.2575 147/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 701us/step - accuracy: 0.9056 - loss: 0.2576 222/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 690us/step - accuracy: 0.9029 - loss: 0.2651 295/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 690us/step - accuracy: 0.9021 - loss: 0.2683 296/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 691us/step - accuracy: 0.9021 - loss: 0.2683 370/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 688us/step - accuracy: 0.9018 - loss: 0.2702 371/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 688us/step - accuracy: 0.9018 - loss: 0.2702 447/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 684us/step - accuracy: 0.9014 - loss: 0.2718 448/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 685us/step - accuracy: 0.9014 - loss: 0.2719 522/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 684us/step - accuracy: 0.9013 - loss: 0.2727 523/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 684us/step - accuracy: 0.9012 - loss: 0.2727 597/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 684us/step - accuracy: 0.9012 - loss: 0.2732 598/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 685us/step - accuracy: 0.9012 - loss: 0.2732 672/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 684us/step - accuracy: 0.9013 - loss: 0.2734 673/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 685us/step - accuracy: 0.9013 - loss: 0.2734 745/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 686us/step - accuracy: 0.9013 - loss: 0.2735 746/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 686us/step - accuracy: 0.9013 - loss: 0.2735 819/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 687us/step - accuracy: 0.9013 - loss: 0.2738 820/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 687us/step - accuracy: 0.9013 - loss: 0.2738 894/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 687us/step - accuracy: 0.9012 - loss: 0.2741 895/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 687us/step - accuracy: 0.9012 - loss: 0.2741 970/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 686us/step - accuracy: 0.9012 - loss: 0.2742 971/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 686us/step - accuracy: 0.9012 - loss: 0.27421046/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 685us/step - accuracy: 0.9012 - loss: 0.27431119/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 685us/step - accuracy: 0.9013 - loss: 0.27421120/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 685us/step - accuracy: 0.9013 - loss: 0.27421194/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 685us/step - accuracy: 0.9013 - loss: 0.27411269/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 684us/step - accuracy: 0.9013 - loss: 0.27411343/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 684us/step - accuracy: 0.9014 - loss: 0.27411416/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 684us/step - accuracy: 0.9014 - loss: 0.27401417/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 684us/step - accuracy: 0.9014 - loss: 0.27401489/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 685us/step - accuracy: 0.9015 - loss: 0.27391490/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 685us/step - accuracy: 0.9015 - loss: 0.27391563/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 686us/step - accuracy: 0.9015 - loss: 0.27391564/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 686us/step - accuracy: 0.9015 - loss: 0.27391640/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 685us/step - accuracy: 0.9015 - loss: 0.27381641/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 685us/step - accuracy: 0.9015 - loss: 0.27381716/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 684us/step - accuracy: 0.9015 - loss: 0.27381717/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 684us/step - accuracy: 0.9015 - loss: 0.27381719/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 725us/step - accuracy: 0.9015 - loss: 0.2738 - val_accuracy: 0.8730 - val_loss: 0.3495
Epoch 20/30
   1/1719 ━━━━━━━━━━━━━━━━━━━━ 18s 11ms/step - accuracy: 0.9688 - loss: 0.2242  74/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 689us/step - accuracy: 0.9128 - loss: 0.2370  75/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 690us/step - accuracy: 0.9127 - loss: 0.2372 148/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 690us/step - accuracy: 0.9064 - loss: 0.2523 149/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 691us/step - accuracy: 0.9063 - loss: 0.2524 222/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 691us/step - accuracy: 0.9039 - loss: 0.2597 223/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 692us/step - accuracy: 0.9039 - loss: 0.2597 282/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 725us/step - accuracy: 0.9034 - loss: 0.2624 283/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 727us/step - accuracy: 0.9033 - loss: 0.2625 347/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 738us/step - accuracy: 0.9031 - loss: 0.2642 348/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 739us/step - accuracy: 0.9031 - loss: 0.2643 411/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 748us/step - accuracy: 0.9028 - loss: 0.2658 412/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 749us/step - accuracy: 0.9027 - loss: 0.2659 475/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 755us/step - accuracy: 0.9026 - loss: 0.2668 476/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 756us/step - accuracy: 0.9026 - loss: 0.2668 542/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 757us/step - accuracy: 0.9026 - loss: 0.2675 607/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 759us/step - accuracy: 0.9026 - loss: 0.2679 672/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 760us/step - accuracy: 0.9027 - loss: 0.2680 673/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 761us/step - accuracy: 0.9027 - loss: 0.2680 743/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 756us/step - accuracy: 0.9028 - loss: 0.2682 744/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 757us/step - accuracy: 0.9028 - loss: 0.2682 816/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 752us/step - accuracy: 0.9028 - loss: 0.2684 817/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 752us/step - accuracy: 0.9028 - loss: 0.2684 889/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 748us/step - accuracy: 0.9028 - loss: 0.2687 890/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 748us/step - accuracy: 0.9028 - loss: 0.2687 960/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 746us/step - accuracy: 0.9028 - loss: 0.2689 961/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 746us/step - accuracy: 0.9028 - loss: 0.26891035/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 741us/step - accuracy: 0.9028 - loss: 0.26891109/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 737us/step - accuracy: 0.9028 - loss: 0.26891183/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 734us/step - accuracy: 0.9029 - loss: 0.26881184/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 734us/step - accuracy: 0.9029 - loss: 0.26881260/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 729us/step - accuracy: 0.9029 - loss: 0.26881332/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 728us/step - accuracy: 0.9029 - loss: 0.26881333/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 728us/step - accuracy: 0.9029 - loss: 0.26871407/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 725us/step - accuracy: 0.9030 - loss: 0.26871408/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 725us/step - accuracy: 0.9030 - loss: 0.26871482/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 723us/step - accuracy: 0.9030 - loss: 0.26861555/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 722us/step - accuracy: 0.9030 - loss: 0.26861556/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 722us/step - accuracy: 0.9030 - loss: 0.26861630/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 720us/step - accuracy: 0.9031 - loss: 0.26851631/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 720us/step - accuracy: 0.9031 - loss: 0.26851703/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 719us/step - accuracy: 0.9031 - loss: 0.26851704/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 719us/step - accuracy: 0.9031 - loss: 0.26851719/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 760us/step - accuracy: 0.9031 - loss: 0.2685 - val_accuracy: 0.8736 - val_loss: 0.3526
Epoch 21/30
   1/1719 ━━━━━━━━━━━━━━━━━━━━ 18s 11ms/step - accuracy: 0.9688 - loss: 0.2288  73/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 695us/step - accuracy: 0.9157 - loss: 0.2334 145/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 695us/step - accuracy: 0.9090 - loss: 0.2474 146/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 696us/step - accuracy: 0.9089 - loss: 0.2476 221/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 688us/step - accuracy: 0.9063 - loss: 0.2550 222/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 688us/step - accuracy: 0.9062 - loss: 0.2551 295/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 688us/step - accuracy: 0.9053 - loss: 0.2582 296/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 688us/step - accuracy: 0.9053 - loss: 0.2582 371/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 685us/step - accuracy: 0.9049 - loss: 0.2601 372/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 686us/step - accuracy: 0.9049 - loss: 0.2601 445/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 686us/step - accuracy: 0.9045 - loss: 0.2616 446/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 687us/step - accuracy: 0.9045 - loss: 0.2617 520/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 685us/step - accuracy: 0.9044 - loss: 0.2625 594/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 684us/step - accuracy: 0.9043 - loss: 0.2629 595/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 684us/step - accuracy: 0.9043 - loss: 0.2629 670/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 683us/step - accuracy: 0.9044 - loss: 0.2631 742/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 684us/step - accuracy: 0.9045 - loss: 0.2632 743/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 684us/step - accuracy: 0.9045 - loss: 0.2632 817/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 684us/step - accuracy: 0.9046 - loss: 0.2634 891/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 684us/step - accuracy: 0.9046 - loss: 0.2638 892/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 684us/step - accuracy: 0.9046 - loss: 0.2638 967/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 683us/step - accuracy: 0.9046 - loss: 0.26391041/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 684us/step - accuracy: 0.9046 - loss: 0.26391042/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 684us/step - accuracy: 0.9046 - loss: 0.26391115/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 684us/step - accuracy: 0.9047 - loss: 0.26381187/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 685us/step - accuracy: 0.9047 - loss: 0.26381188/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 685us/step - accuracy: 0.9047 - loss: 0.26381263/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 684us/step - accuracy: 0.9047 - loss: 0.26381333/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 686us/step - accuracy: 0.9047 - loss: 0.26371334/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 686us/step - accuracy: 0.9047 - loss: 0.26371406/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 687us/step - accuracy: 0.9048 - loss: 0.26361407/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 687us/step - accuracy: 0.9048 - loss: 0.26361480/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 687us/step - accuracy: 0.9048 - loss: 0.26361481/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 688us/step - accuracy: 0.9048 - loss: 0.26361552/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 689us/step - accuracy: 0.9048 - loss: 0.26351553/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 689us/step - accuracy: 0.9048 - loss: 0.26351554/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 689us/step - accuracy: 0.9048 - loss: 0.26351627/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 689us/step - accuracy: 0.9048 - loss: 0.26351628/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 689us/step - accuracy: 0.9048 - loss: 0.26351700/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 689us/step - accuracy: 0.9048 - loss: 0.26351701/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 689us/step - accuracy: 0.9048 - loss: 0.26351719/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 730us/step - accuracy: 0.9048 - loss: 0.2635 - val_accuracy: 0.8736 - val_loss: 0.3512
Epoch 22/30
   1/1719 ━━━━━━━━━━━━━━━━━━━━ 18s 11ms/step - accuracy: 0.9688 - loss: 0.2227  74/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 687us/step - accuracy: 0.9191 - loss: 0.2284  75/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 688us/step - accuracy: 0.9190 - loss: 0.2286 148/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 690us/step - accuracy: 0.9113 - loss: 0.2427 222/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 686us/step - accuracy: 0.9083 - loss: 0.2499 296/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 684us/step - accuracy: 0.9072 - loss: 0.2531 371/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 681us/step - accuracy: 0.9066 - loss: 0.2550 372/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 681us/step - accuracy: 0.9066 - loss: 0.2550 444/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 683us/step - accuracy: 0.9062 - loss: 0.2565 445/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 683us/step - accuracy: 0.9062 - loss: 0.2565 518/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 684us/step - accuracy: 0.9060 - loss: 0.2574 591/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 684us/step - accuracy: 0.9060 - loss: 0.2579 592/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 684us/step - accuracy: 0.9060 - loss: 0.2579 664/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 685us/step - accuracy: 0.9061 - loss: 0.2580 737/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 686us/step - accuracy: 0.9062 - loss: 0.2582 738/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 686us/step - accuracy: 0.9062 - loss: 0.2582 812/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 686us/step - accuracy: 0.9063 - loss: 0.2584 813/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 686us/step - accuracy: 0.9063 - loss: 0.2584 885/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 687us/step - accuracy: 0.9063 - loss: 0.2587 886/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 687us/step - accuracy: 0.9063 - loss: 0.2587 958/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 688us/step - accuracy: 0.9063 - loss: 0.2589 959/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 688us/step - accuracy: 0.9063 - loss: 0.25891032/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 688us/step - accuracy: 0.9064 - loss: 0.25891105/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 689us/step - accuracy: 0.9064 - loss: 0.25881179/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 688us/step - accuracy: 0.9065 - loss: 0.25881252/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 688us/step - accuracy: 0.9065 - loss: 0.25881253/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 688us/step - accuracy: 0.9065 - loss: 0.25881324/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 689us/step - accuracy: 0.9066 - loss: 0.25881325/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 689us/step - accuracy: 0.9066 - loss: 0.25881399/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 689us/step - accuracy: 0.9066 - loss: 0.25871470/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 690us/step - accuracy: 0.9066 - loss: 0.25861543/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 690us/step - accuracy: 0.9067 - loss: 0.25861544/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 690us/step - accuracy: 0.9067 - loss: 0.25861615/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 691us/step - accuracy: 0.9067 - loss: 0.25861616/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 691us/step - accuracy: 0.9067 - loss: 0.25861689/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 691us/step - accuracy: 0.9067 - loss: 0.25861690/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 691us/step - accuracy: 0.9067 - loss: 0.25861719/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 734us/step - accuracy: 0.9067 - loss: 0.2586 - val_accuracy: 0.8738 - val_loss: 0.3527
Epoch 23/30
   1/1719 ━━━━━━━━━━━━━━━━━━━━ 19s 11ms/step - accuracy: 0.9375 - loss: 0.2213  70/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 728us/step - accuracy: 0.9199 - loss: 0.2238  71/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 729us/step - accuracy: 0.9199 - loss: 0.2240 143/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 712us/step - accuracy: 0.9138 - loss: 0.2374 216/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 704us/step - accuracy: 0.9110 - loss: 0.2449 217/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 705us/step - accuracy: 0.9109 - loss: 0.2449 289/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 703us/step - accuracy: 0.9099 - loss: 0.2482 290/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 704us/step - accuracy: 0.9098 - loss: 0.2482 363/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 702us/step - accuracy: 0.9093 - loss: 0.2501 364/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 702us/step - accuracy: 0.9093 - loss: 0.2501 439/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 698us/step - accuracy: 0.9089 - loss: 0.2517 440/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 698us/step - accuracy: 0.9089 - loss: 0.2517 512/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 698us/step - accuracy: 0.9087 - loss: 0.2525 513/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 698us/step - accuracy: 0.9087 - loss: 0.2525 584/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 700us/step - accuracy: 0.9086 - loss: 0.2530 654/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 702us/step - accuracy: 0.9087 - loss: 0.2531 655/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 702us/step - accuracy: 0.9087 - loss: 0.2531 729/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 700us/step - accuracy: 0.9088 - loss: 0.2533 802/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 699us/step - accuracy: 0.9089 - loss: 0.2535 873/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 700us/step - accuracy: 0.9089 - loss: 0.2538 874/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 700us/step - accuracy: 0.9089 - loss: 0.2538 944/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 701us/step - accuracy: 0.9089 - loss: 0.2540 945/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 701us/step - accuracy: 0.9089 - loss: 0.25401018/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 701us/step - accuracy: 0.9089 - loss: 0.25411092/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 699us/step - accuracy: 0.9090 - loss: 0.25401093/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 700us/step - accuracy: 0.9090 - loss: 0.25401164/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 700us/step - accuracy: 0.9090 - loss: 0.25401165/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 701us/step - accuracy: 0.9090 - loss: 0.25401238/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 700us/step - accuracy: 0.9090 - loss: 0.25391310/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 700us/step - accuracy: 0.9090 - loss: 0.25391311/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 700us/step - accuracy: 0.9090 - loss: 0.25391385/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 699us/step - accuracy: 0.9090 - loss: 0.25391460/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 698us/step - accuracy: 0.9090 - loss: 0.25381461/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 698us/step - accuracy: 0.9090 - loss: 0.25381536/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 697us/step - accuracy: 0.9090 - loss: 0.25381537/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 697us/step - accuracy: 0.9090 - loss: 0.25381610/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 697us/step - accuracy: 0.9090 - loss: 0.25381611/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 697us/step - accuracy: 0.9090 - loss: 0.25381684/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 697us/step - accuracy: 0.9090 - loss: 0.25381685/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 697us/step - accuracy: 0.9090 - loss: 0.25381719/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 737us/step - accuracy: 0.9090 - loss: 0.2538 - val_accuracy: 0.8728 - val_loss: 0.3510
Epoch 24/30
   1/1719 ━━━━━━━━━━━━━━━━━━━━ 18s 11ms/step - accuracy: 0.9375 - loss: 0.2117   2/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 743us/step - accuracy: 0.9375 - loss: 0.2079  73/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 710us/step - accuracy: 0.9202 - loss: 0.2195  74/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 713us/step - accuracy: 0.9201 - loss: 0.2197 148/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 696us/step - accuracy: 0.9144 - loss: 0.2334 149/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 697us/step - accuracy: 0.9144 - loss: 0.2336 222/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 694us/step - accuracy: 0.9120 - loss: 0.2404 300/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 682us/step - accuracy: 0.9111 - loss: 0.2437 301/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 682us/step - accuracy: 0.9111 - loss: 0.2437 376/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 681us/step - accuracy: 0.9106 - loss: 0.2455 377/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 681us/step - accuracy: 0.9106 - loss: 0.2456 450/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 683us/step - accuracy: 0.9102 - loss: 0.2471 451/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 683us/step - accuracy: 0.9102 - loss: 0.2471 525/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 683us/step - accuracy: 0.9100 - loss: 0.2479 526/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 683us/step - accuracy: 0.9100 - loss: 0.2479 601/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 681us/step - accuracy: 0.9100 - loss: 0.2483 676/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 680us/step - accuracy: 0.9101 - loss: 0.2484 753/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 678us/step - accuracy: 0.9102 - loss: 0.2486 754/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 678us/step - accuracy: 0.9102 - loss: 0.2486 829/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 677us/step - accuracy: 0.9102 - loss: 0.2489 830/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 677us/step - accuracy: 0.9102 - loss: 0.2489 901/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 680us/step - accuracy: 0.9102 - loss: 0.2492 973/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 681us/step - accuracy: 0.9103 - loss: 0.24931048/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 681us/step - accuracy: 0.9103 - loss: 0.24931121/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 681us/step - accuracy: 0.9104 - loss: 0.24921122/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 681us/step - accuracy: 0.9104 - loss: 0.24921196/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 681us/step - accuracy: 0.9104 - loss: 0.24921197/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 681us/step - accuracy: 0.9104 - loss: 0.24921270/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 682us/step - accuracy: 0.9104 - loss: 0.24921271/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 682us/step - accuracy: 0.9104 - loss: 0.24921346/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 681us/step - accuracy: 0.9104 - loss: 0.24921347/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 681us/step - accuracy: 0.9104 - loss: 0.24921420/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 682us/step - accuracy: 0.9104 - loss: 0.24911495/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 681us/step - accuracy: 0.9105 - loss: 0.24911496/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 681us/step - accuracy: 0.9105 - loss: 0.24911568/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 682us/step - accuracy: 0.9105 - loss: 0.24911569/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 682us/step - accuracy: 0.9105 - loss: 0.24911640/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 683us/step - accuracy: 0.9105 - loss: 0.24901641/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 683us/step - accuracy: 0.9105 - loss: 0.24901712/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 684us/step - accuracy: 0.9105 - loss: 0.24911713/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 684us/step - accuracy: 0.9105 - loss: 0.24911719/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 726us/step - accuracy: 0.9105 - loss: 0.2491 - val_accuracy: 0.8754 - val_loss: 0.3521
Epoch 25/30
   1/1719 ━━━━━━━━━━━━━━━━━━━━ 18s 11ms/step - accuracy: 0.9375 - loss: 0.2039  72/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 711us/step - accuracy: 0.9211 - loss: 0.2161  73/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 713us/step - accuracy: 0.9210 - loss: 0.2163 145/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 704us/step - accuracy: 0.9159 - loss: 0.2294 219/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 697us/step - accuracy: 0.9137 - loss: 0.2365 220/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 697us/step - accuracy: 0.9137 - loss: 0.2366 295/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 691us/step - accuracy: 0.9129 - loss: 0.2397 296/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 691us/step - accuracy: 0.9129 - loss: 0.2397 372/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 686us/step - accuracy: 0.9125 - loss: 0.2416 445/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 687us/step - accuracy: 0.9122 - loss: 0.2430 446/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 687us/step - accuracy: 0.9122 - loss: 0.2431 518/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 689us/step - accuracy: 0.9122 - loss: 0.2438 519/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 689us/step - accuracy: 0.9122 - loss: 0.2438 590/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 692us/step - accuracy: 0.9122 - loss: 0.2442 664/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 690us/step - accuracy: 0.9124 - loss: 0.2443 737/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 691us/step - accuracy: 0.9125 - loss: 0.2445 808/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 692us/step - accuracy: 0.9126 - loss: 0.2447 881/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 693us/step - accuracy: 0.9126 - loss: 0.2450 882/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 693us/step - accuracy: 0.9126 - loss: 0.2450 956/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 692us/step - accuracy: 0.9126 - loss: 0.24511028/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 692us/step - accuracy: 0.9127 - loss: 0.24511029/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 692us/step - accuracy: 0.9127 - loss: 0.24511099/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 694us/step - accuracy: 0.9127 - loss: 0.24511100/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 694us/step - accuracy: 0.9127 - loss: 0.24511172/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 694us/step - accuracy: 0.9127 - loss: 0.24501173/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 694us/step - accuracy: 0.9127 - loss: 0.24501174/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 695us/step - accuracy: 0.9127 - loss: 0.24501246/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 695us/step - accuracy: 0.9127 - loss: 0.24501247/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 695us/step - accuracy: 0.9127 - loss: 0.24501318/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 696us/step - accuracy: 0.9128 - loss: 0.24501391/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 696us/step - accuracy: 0.9128 - loss: 0.24491464/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 695us/step - accuracy: 0.9128 - loss: 0.24491465/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 695us/step - accuracy: 0.9128 - loss: 0.24491538/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 695us/step - accuracy: 0.9129 - loss: 0.24481610/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 695us/step - accuracy: 0.9129 - loss: 0.24481611/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 695us/step - accuracy: 0.9129 - loss: 0.24481683/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 695us/step - accuracy: 0.9129 - loss: 0.24481684/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 695us/step - accuracy: 0.9129 - loss: 0.24481719/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 736us/step - accuracy: 0.9129 - loss: 0.2448 - val_accuracy: 0.8758 - val_loss: 0.3532
Epoch 26/30
   1/1719 ━━━━━━━━━━━━━━━━━━━━ 20s 12ms/step - accuracy: 0.9375 - loss: 0.2000  73/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 700us/step - accuracy: 0.9235 - loss: 0.2114  74/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 704us/step - accuracy: 0.9234 - loss: 0.2115 146/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 700us/step - accuracy: 0.9178 - loss: 0.2245 147/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 701us/step - accuracy: 0.9178 - loss: 0.2247 221/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 693us/step - accuracy: 0.9157 - loss: 0.2316 222/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 694us/step - accuracy: 0.9157 - loss: 0.2317 298/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 687us/step - accuracy: 0.9149 - loss: 0.2349 372/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 685us/step - accuracy: 0.9145 - loss: 0.2367 373/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 686us/step - accuracy: 0.9145 - loss: 0.2367 446/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 687us/step - accuracy: 0.9142 - loss: 0.2382 447/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 687us/step - accuracy: 0.9142 - loss: 0.2382 521/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 685us/step - accuracy: 0.9141 - loss: 0.2390 596/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 684us/step - accuracy: 0.9141 - loss: 0.2395 597/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 684us/step - accuracy: 0.9141 - loss: 0.2395 673/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 682us/step - accuracy: 0.9142 - loss: 0.2396 674/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 682us/step - accuracy: 0.9142 - loss: 0.2396 746/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 684us/step - accuracy: 0.9143 - loss: 0.2397 747/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 684us/step - accuracy: 0.9143 - loss: 0.2397 820/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 685us/step - accuracy: 0.9143 - loss: 0.2400 821/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 685us/step - accuracy: 0.9143 - loss: 0.2400 891/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 688us/step - accuracy: 0.9143 - loss: 0.2403 892/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 688us/step - accuracy: 0.9143 - loss: 0.2403 967/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 687us/step - accuracy: 0.9143 - loss: 0.2404 968/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 687us/step - accuracy: 0.9143 - loss: 0.24041040/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 688us/step - accuracy: 0.9143 - loss: 0.24051041/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 688us/step - accuracy: 0.9143 - loss: 0.24051112/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 689us/step - accuracy: 0.9143 - loss: 0.24041186/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 688us/step - accuracy: 0.9143 - loss: 0.24041260/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 688us/step - accuracy: 0.9143 - loss: 0.24041261/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 688us/step - accuracy: 0.9143 - loss: 0.24041334/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 689us/step - accuracy: 0.9143 - loss: 0.24031407/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 689us/step - accuracy: 0.9143 - loss: 0.24031408/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 689us/step - accuracy: 0.9143 - loss: 0.24031478/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 690us/step - accuracy: 0.9143 - loss: 0.24031479/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 691us/step - accuracy: 0.9143 - loss: 0.24031551/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 691us/step - accuracy: 0.9143 - loss: 0.24021552/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 691us/step - accuracy: 0.9143 - loss: 0.24021623/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 692us/step - accuracy: 0.9143 - loss: 0.24021624/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 692us/step - accuracy: 0.9143 - loss: 0.24021696/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 692us/step - accuracy: 0.9143 - loss: 0.24021697/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 692us/step - accuracy: 0.9143 - loss: 0.24021719/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 734us/step - accuracy: 0.9143 - loss: 0.2402 - val_accuracy: 0.8756 - val_loss: 0.3532
Epoch 27/30
   1/1719 ━━━━━━━━━━━━━━━━━━━━ 18s 11ms/step - accuracy: 0.9375 - loss: 0.1953  74/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 687us/step - accuracy: 0.9257 - loss: 0.2078 149/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 680us/step - accuracy: 0.9206 - loss: 0.2210 223/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 680us/step - accuracy: 0.9187 - loss: 0.2276 224/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 680us/step - accuracy: 0.9187 - loss: 0.2276 299/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 679us/step - accuracy: 0.9178 - loss: 0.2307 300/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 679us/step - accuracy: 0.9178 - loss: 0.2307 371/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 685us/step - accuracy: 0.9174 - loss: 0.2324 372/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 686us/step - accuracy: 0.9174 - loss: 0.2324 445/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 687us/step - accuracy: 0.9170 - loss: 0.2340 446/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 687us/step - accuracy: 0.9170 - loss: 0.2340 517/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 690us/step - accuracy: 0.9168 - loss: 0.2348 518/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 690us/step - accuracy: 0.9168 - loss: 0.2348 591/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 690us/step - accuracy: 0.9167 - loss: 0.2352 664/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 690us/step - accuracy: 0.9168 - loss: 0.2353 665/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 690us/step - accuracy: 0.9168 - loss: 0.2353 738/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 690us/step - accuracy: 0.9168 - loss: 0.2355 739/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 690us/step - accuracy: 0.9168 - loss: 0.2355 812/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 690us/step - accuracy: 0.9168 - loss: 0.2357 813/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 690us/step - accuracy: 0.9168 - loss: 0.2357 885/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 691us/step - accuracy: 0.9167 - loss: 0.2360 886/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 691us/step - accuracy: 0.9167 - loss: 0.2360 961/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 690us/step - accuracy: 0.9167 - loss: 0.2362 962/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 690us/step - accuracy: 0.9166 - loss: 0.23621037/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 688us/step - accuracy: 0.9166 - loss: 0.23621109/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 689us/step - accuracy: 0.9166 - loss: 0.23621110/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 689us/step - accuracy: 0.9166 - loss: 0.23621184/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 689us/step - accuracy: 0.9166 - loss: 0.23611185/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 689us/step - accuracy: 0.9166 - loss: 0.23611254/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 691us/step - accuracy: 0.9165 - loss: 0.23611255/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 691us/step - accuracy: 0.9165 - loss: 0.23611324/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 693us/step - accuracy: 0.9165 - loss: 0.23611395/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 694us/step - accuracy: 0.9165 - loss: 0.23611396/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 694us/step - accuracy: 0.9165 - loss: 0.23611467/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 695us/step - accuracy: 0.9165 - loss: 0.23601468/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 695us/step - accuracy: 0.9165 - loss: 0.23601540/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 695us/step - accuracy: 0.9165 - loss: 0.23601541/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 696us/step - accuracy: 0.9165 - loss: 0.23601614/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 695us/step - accuracy: 0.9165 - loss: 0.23601686/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 695us/step - accuracy: 0.9164 - loss: 0.23601687/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 695us/step - accuracy: 0.9164 - loss: 0.23601688/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 695us/step - accuracy: 0.9164 - loss: 0.23601719/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 737us/step - accuracy: 0.9164 - loss: 0.2360 - val_accuracy: 0.8766 - val_loss: 0.3517
Epoch 28/30
   1/1719 ━━━━━━━━━━━━━━━━━━━━ 20s 12ms/step - accuracy: 0.9375 - loss: 0.1926  69/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 742us/step - accuracy: 0.9277 - loss: 0.2029  70/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 747us/step - accuracy: 0.9276 - loss: 0.2030 139/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 739us/step - accuracy: 0.9230 - loss: 0.2150 210/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 730us/step - accuracy: 0.9208 - loss: 0.2224 211/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 731us/step - accuracy: 0.9208 - loss: 0.2225 282/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 725us/step - accuracy: 0.9198 - loss: 0.2259 354/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 721us/step - accuracy: 0.9194 - loss: 0.2278 355/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 721us/step - accuracy: 0.9193 - loss: 0.2278 425/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 721us/step - accuracy: 0.9189 - loss: 0.2294 497/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 718us/step - accuracy: 0.9187 - loss: 0.2304 569/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 716us/step - accuracy: 0.9185 - loss: 0.2310 641/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 715us/step - accuracy: 0.9186 - loss: 0.2311 642/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 715us/step - accuracy: 0.9186 - loss: 0.2311 715/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 712us/step - accuracy: 0.9186 - loss: 0.2313 716/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 712us/step - accuracy: 0.9186 - loss: 0.2313 786/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 714us/step - accuracy: 0.9186 - loss: 0.2315 787/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 714us/step - accuracy: 0.9186 - loss: 0.2315 858/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 713us/step - accuracy: 0.9186 - loss: 0.2318 859/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 713us/step - accuracy: 0.9186 - loss: 0.2318 933/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 711us/step - accuracy: 0.9186 - loss: 0.23201006/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 709us/step - accuracy: 0.9186 - loss: 0.23211007/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 709us/step - accuracy: 0.9186 - loss: 0.23211080/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 708us/step - accuracy: 0.9186 - loss: 0.23211081/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 708us/step - accuracy: 0.9186 - loss: 0.23211154/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 707us/step - accuracy: 0.9186 - loss: 0.23201228/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 706us/step - accuracy: 0.9186 - loss: 0.23201229/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 706us/step - accuracy: 0.9186 - loss: 0.23201302/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 705us/step - accuracy: 0.9185 - loss: 0.23201303/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 705us/step - accuracy: 0.9185 - loss: 0.23201374/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 705us/step - accuracy: 0.9186 - loss: 0.23201375/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 705us/step - accuracy: 0.9186 - loss: 0.23201446/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 706us/step - accuracy: 0.9186 - loss: 0.23191447/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 706us/step - accuracy: 0.9186 - loss: 0.23191521/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 705us/step - accuracy: 0.9185 - loss: 0.23191522/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 705us/step - accuracy: 0.9185 - loss: 0.23191597/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 703us/step - accuracy: 0.9185 - loss: 0.23191598/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 703us/step - accuracy: 0.9185 - loss: 0.23191671/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 703us/step - accuracy: 0.9185 - loss: 0.23191672/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 703us/step - accuracy: 0.9185 - loss: 0.23191719/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 745us/step - accuracy: 0.9185 - loss: 0.2319 - val_accuracy: 0.8782 - val_loss: 0.3515
Epoch 29/30
   1/1719 ━━━━━━━━━━━━━━━━━━━━ 19s 11ms/step - accuracy: 0.9375 - loss: 0.1866   2/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 820us/step - accuracy: 0.9375 - loss: 0.1856  75/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 692us/step - accuracy: 0.9290 - loss: 0.2001  76/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 694us/step - accuracy: 0.9289 - loss: 0.2002 149/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 692us/step - accuracy: 0.9239 - loss: 0.2126 150/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 693us/step - accuracy: 0.9239 - loss: 0.2127 224/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 688us/step - accuracy: 0.9218 - loss: 0.2190 225/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 688us/step - accuracy: 0.9218 - loss: 0.2191 300/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 684us/step - accuracy: 0.9209 - loss: 0.2221 301/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 684us/step - accuracy: 0.9209 - loss: 0.2221 378/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 679us/step - accuracy: 0.9204 - loss: 0.2240 379/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 679us/step - accuracy: 0.9204 - loss: 0.2240 455/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 677us/step - accuracy: 0.9199 - loss: 0.2256 456/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 677us/step - accuracy: 0.9199 - loss: 0.2256 531/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 676us/step - accuracy: 0.9197 - loss: 0.2264 532/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 676us/step - accuracy: 0.9197 - loss: 0.2264 608/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 675us/step - accuracy: 0.9197 - loss: 0.2268 680/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 677us/step - accuracy: 0.9198 - loss: 0.2269 681/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 678us/step - accuracy: 0.9198 - loss: 0.2269 755/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 678us/step - accuracy: 0.9198 - loss: 0.2271 756/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 678us/step - accuracy: 0.9198 - loss: 0.2271 831/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 678us/step - accuracy: 0.9197 - loss: 0.2274 907/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 676us/step - accuracy: 0.9197 - loss: 0.2277 983/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 675us/step - accuracy: 0.9197 - loss: 0.2278 984/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 676us/step - accuracy: 0.9197 - loss: 0.22781058/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 676us/step - accuracy: 0.9197 - loss: 0.22791059/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 676us/step - accuracy: 0.9197 - loss: 0.22791132/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 677us/step - accuracy: 0.9197 - loss: 0.22781206/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 677us/step - accuracy: 0.9197 - loss: 0.22781281/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 677us/step - accuracy: 0.9197 - loss: 0.22781357/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 676us/step - accuracy: 0.9197 - loss: 0.22781358/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 676us/step - accuracy: 0.9197 - loss: 0.22781432/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 676us/step - accuracy: 0.9197 - loss: 0.22771433/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 676us/step - accuracy: 0.9197 - loss: 0.22771506/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 677us/step - accuracy: 0.9197 - loss: 0.22771507/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 677us/step - accuracy: 0.9197 - loss: 0.22771583/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 676us/step - accuracy: 0.9197 - loss: 0.22771584/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 676us/step - accuracy: 0.9197 - loss: 0.22771660/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 676us/step - accuracy: 0.9197 - loss: 0.22771719/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 716us/step - accuracy: 0.9196 - loss: 0.2278 - val_accuracy: 0.8764 - val_loss: 0.3508
Epoch 30/30
   1/1719 ━━━━━━━━━━━━━━━━━━━━ 18s 11ms/step - accuracy: 0.9375 - loss: 0.1789  74/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 691us/step - accuracy: 0.9289 - loss: 0.1960  75/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 692us/step - accuracy: 0.9288 - loss: 0.1962 150/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 680us/step - accuracy: 0.9248 - loss: 0.2090 226/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 675us/step - accuracy: 0.9228 - loss: 0.2155 227/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 676us/step - accuracy: 0.9228 - loss: 0.2156 301/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 676us/step - accuracy: 0.9221 - loss: 0.2185 376/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 675us/step - accuracy: 0.9217 - loss: 0.2203 377/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 675us/step - accuracy: 0.9217 - loss: 0.2203 446/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 685us/step - accuracy: 0.9213 - loss: 0.2218 447/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 685us/step - accuracy: 0.9213 - loss: 0.2218 514/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 694us/step - accuracy: 0.9212 - loss: 0.2226 515/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 695us/step - accuracy: 0.9212 - loss: 0.2226 585/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 697us/step - accuracy: 0.9211 - loss: 0.2231 586/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 698us/step - accuracy: 0.9211 - loss: 0.2231 654/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 703us/step - accuracy: 0.9211 - loss: 0.2232 655/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 703us/step - accuracy: 0.9211 - loss: 0.2232 724/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 705us/step - accuracy: 0.9211 - loss: 0.2233 725/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 706us/step - accuracy: 0.9211 - loss: 0.2233 791/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 710us/step - accuracy: 0.9211 - loss: 0.2235 858/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 714us/step - accuracy: 0.9211 - loss: 0.2238 859/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 714us/step - accuracy: 0.9211 - loss: 0.2238 928/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 715us/step - accuracy: 0.9210 - loss: 0.2240 929/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 715us/step - accuracy: 0.9210 - loss: 0.2240 997/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 717us/step - accuracy: 0.9210 - loss: 0.2241 998/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 718us/step - accuracy: 0.9210 - loss: 0.22411065/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 720us/step - accuracy: 0.9210 - loss: 0.22411066/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 720us/step - accuracy: 0.9210 - loss: 0.22411136/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 720us/step - accuracy: 0.9210 - loss: 0.22411207/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 719us/step - accuracy: 0.9210 - loss: 0.22401208/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 720us/step - accuracy: 0.9210 - loss: 0.22401279/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 719us/step - accuracy: 0.9210 - loss: 0.22401349/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 719us/step - accuracy: 0.9210 - loss: 0.22401350/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 719us/step - accuracy: 0.9210 - loss: 0.22401422/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 719us/step - accuracy: 0.9210 - loss: 0.22401423/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 719us/step - accuracy: 0.9210 - loss: 0.22401494/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 718us/step - accuracy: 0.9210 - loss: 0.22401495/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 718us/step - accuracy: 0.9210 - loss: 0.22401569/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 717us/step - accuracy: 0.9210 - loss: 0.22401570/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 717us/step - accuracy: 0.9210 - loss: 0.22401640/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 717us/step - accuracy: 0.9210 - loss: 0.22401641/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 717us/step - accuracy: 0.9210 - loss: 0.22401715/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 715us/step - accuracy: 0.9209 - loss: 0.22401716/1719 ━━━━━━━━━━━━━━━━━━━━ 0s 715us/step - accuracy: 0.9209 - loss: 0.22401719/1719 ━━━━━━━━━━━━━━━━━━━━ 1s 757us/step - accuracy: 0.9209 - loss: 0.2240 - val_accuracy: 0.8778 - val_loss: 0.3505

Le modèle est entraîné avec un ensemble d’entraînement et un ensemble de validation. À chaque étape, le modèle rapporte ses performances sur les deux ensembles. Cela permet également de visualiser les courbes d’exactitude et de perte sur les deux ensembles (plus de détails à venir).

Lors de l’appel à la méthode fit dans Keras (ou des frameworks similaires), chaque étape correspond à l’évaluation d’un mini-lot. Un mini-lot est un sous-ensemble des données d’entraînement, et à chaque étape, le modèle met à jour ses poids en fonction de l’erreur calculée à partir de ce mini-lot.

Une époque est définie comme un passage complet sur l’ensemble des données d’entraînement. Pendant une époque, le modèle traite plusieurs mini-lots jusqu’à avoir vu toutes les données d’entraînement une fois. Ce processus est répété sur un nombre spécifié d’époques pour optimiser les performances du modèle.

Visualisation

import pandas as pd 

pd.DataFrame(history.history).plot(
    figsize=(8, 5), xlim=[0, 29], ylim=[0, 1], grid=True, xlabel="Époque",
    style=["r--", "r--.", "b-", "b-*"])
plt.legend(loc="lower left")  # code supplémentaire
plt.show()

Évaluation du modèle sur l’ensemble de test

model.evaluate(X_test, y_test)

  1/313 ━━━━━━━━━━━━━━━━━━━━ 3s 11ms/step - accuracy: 0.8750 - loss: 0.6662  2/313 ━━━━━━━━━━━━━━━━━━━━ 0s 1ms/step - accuracy: 0.8750 - loss: 0.5559 121/313 ━━━━━━━━━━━━━━━━━━━━ 0s 430us/step - accuracy: 0.8766 - loss: 0.3653122/313 ━━━━━━━━━━━━━━━━━━━━ 0s 431us/step - accuracy: 0.8765 - loss: 0.3655123/313 ━━━━━━━━━━━━━━━━━━━━ 0s 432us/step - accuracy: 0.8765 - loss: 0.3656246/313 ━━━━━━━━━━━━━━━━━━━━ 0s 420us/step - accuracy: 0.8718 - loss: 0.3741247/313 ━━━━━━━━━━━━━━━━━━━━ 0s 420us/step - accuracy: 0.8718 - loss: 0.3741248/313 ━━━━━━━━━━━━━━━━━━━━ 0s 421us/step - accuracy: 0.8718 - loss: 0.3741313/313 ━━━━━━━━━━━━━━━━━━━━ 0s 416us/step - accuracy: 0.8717 - loss: 0.3740

[0.37116000056266785, 0.8726000189781189]

Faire des prédictions

X_new = X_test[:3]
y_proba = model.predict(X_new)
y_proba.round(2)

1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 25ms/step1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 25ms/step

array([[0.  , 0.  , 0.  , 0.  , 0.  , 0.26, 0.  , 0.01, 0.  , 0.73],
       [0.  , 0.  , 1.  , 0.  , 0.  , 0.  , 0.  , 0.  , 0.  , 0.  ],
       [0.  , 1.  , 0.  , 0.  , 0.  , 0.  , 0.  , 0.  , 0.  , 0.  ]],
      dtype=float32)

. . .

y_pred = y_proba.argmax(axis=-1)
y_pred

array([9, 2, 1])

. . .

y_new = y_test[:3]
y_new

array([9, 2, 1], dtype=uint8)

Comme on peut le voir, les prédictions sont sans ambiguïté, avec une seule classe par prédiction présentant une valeur élevée.

Prédictions vs Observations

np.array(class_names)[y_pred]

array(['Botte', 'Pull', 'Pantalon'], dtype='<U11')

Prologue

Résumé

• Introduction aux réseaux de neurones et au connexionnisme
  • Passage de l’IA symbolique aux approches connexionnistes en intelligence artificielle.
  • Inspiration des réseaux neuronaux biologiques et de la structure du cerveau humain.
• Calculs avec neurodes et unités logiques à seuil
  • Modèles précoces de neurones (neurodes) capables de réaliser des opérations logiques (ET, OU, NON).
  • Limites des perceptrons simples dans la résolution de problèmes non linéairement séparables comme le XOR.
• Perceptrons multicouches (MLP) et réseaux de neurones à propagation avant (FNN)
  • Dépassement des limites des perceptrons en introduisant des couches cachées.
  • Structure et flux d’information dans les réseaux de neurones à propagation avant.
  • Explication des calculs de la passe avant dans les réseaux de neurones.
• Fonctions d’activation dans les réseaux de neurones
  • Importance des fonctions d’activation non linéaires (sigmoïde, tanh, ReLU) pour permettre l’apprentissage de motifs complexes.
  • Rôle des fonctions d’activation dans la rétropropagation et l’optimisation par descente de gradient.
  • Théorème de l’approximation universelle et ses implications pour les réseaux neuronaux.
• Frameworks d’apprentissage profond
  • Aperçu de PyTorch et TensorFlow en tant que plateformes leaders pour l’apprentissage profond.
  • Introduction à Keras comme API de haut niveau pour la construction et l’entraînement des réseaux neuronaux.
  • Discussion sur l’adaptabilité des différents frameworks à la recherche et aux applications industrielles.
• Implémentation pratique avec Keras
  • Chargement et exploration de l’ensemble de données Fashion-MNIST.
  • Création d’un modèle de réseau neuronal avec l’API Sequential de Keras.
  • Compilation du modèle avec des fonctions de perte et des optimiseurs appropriés pour la classification multiclasses.
  • Entraînement du modèle et visualisation des métriques d’entraînement et de validation sur les époques.
• Évaluation des performances du modèle sur l’ensemble de test
  • Évaluation des performances du modèle sur l’ensemble de test Fashion-MNIST.
  • Interprétation des résultats obtenus après l’entraînement.
• Faire des prédictions et interpréter les résultats
  • Utilisation du modèle entraîné pour faire des prédictions sur de nouvelles données.
  • Visualisation des prédictions en parallèle avec les images et étiquettes réelles.
  • Compréhension des probabilités de sortie et des assignations de classes dans le contexte de l’ensemble de données.

Prochain cours

• Nous discutons de l’algorithme utilisé pour entraîner les réseaux de neurones artificiels.

Références

Cybenko, George V. 1989. « Approximation by superpositions of a sigmoidal function ». Mathematics of Control, Signals and Systems 2: 303‑14. https://api.semanticscholar.org/CorpusID:3958369.

Géron, Aurélien. 2022. Hands-on Machine Learning with Scikit-Learn, Keras, and TensorFlow. 3ᵉ éd. O’Reilly Media, Inc.

Goodfellow, Ian, Yoshua Bengio, et Aaron Courville. 2016. Deep Learning. Adaptive computation et machine learning. MIT Press. https://dblp.org/rec/books/daglib/0040158.

Hornik, Kurt, Maxwell Stinchcombe, et Halbert White. 1989. « Multilayer feedforward networks are universal approximators ». Neural Networks 2 (5): 359‑66. https://doi.org/https://doi.org/10.1016/0893-6080(89)90020-8.

LeCun, Yann, Yoshua Bengio, et Geoffrey Hinton. 2015. « Deep learning ». Nature 521 (7553): 436‑44. https://doi.org/10.1038/nature14539.

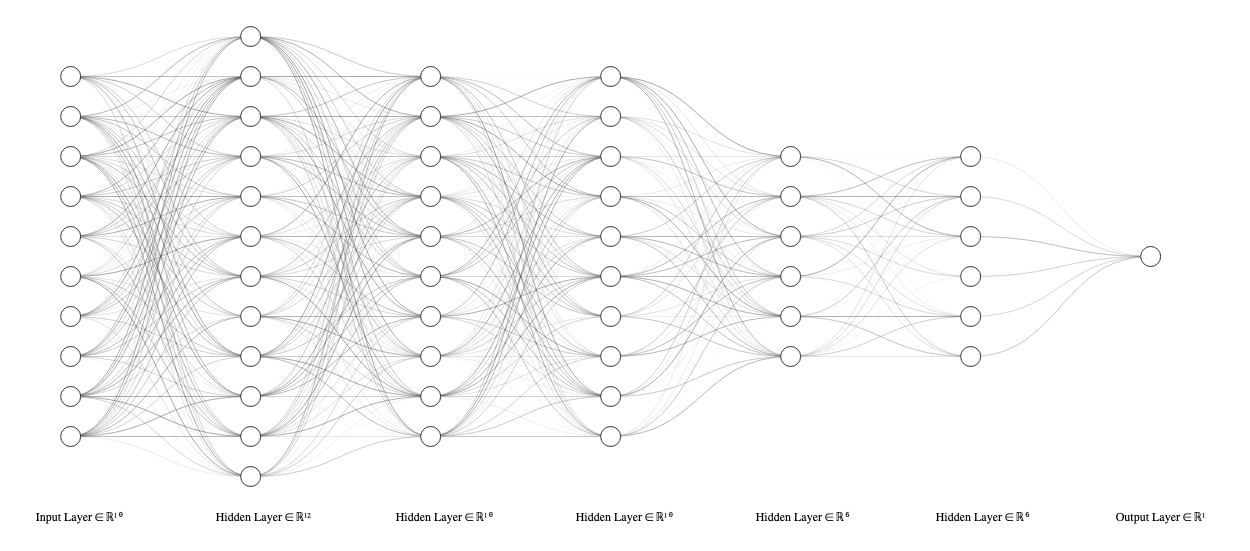
LeNail, Alexander. 2019. « NN-SVG: Publication-Ready Neural Network Architecture Schematics ». Journal of Open Source Software 4 (33): 747. https://doi.org/10.21105/joss.00747.

McCulloch, Warren S, et Walter Pitts. 1943. « A logical calculus of the ideas immanent in nervous activity ». The Bulletin of Mathematical Biophysics 5 (4): 115‑33. https://doi.org/10.1007/bf02478259.

Minsky, Marvin, et Seymour Papert. 1969. Perceptrons: An Introduction to Computational Geometry. Cambridge, MA, USA: MIT Press.

Rosenblatt, F. 1958. « The perceptron: A probabilistic model for information storage and organization in the brain. » Psychological Review 65 (6): 386‑408. https://doi.org/10.1037/h0042519.

Russell, Stuart, et Peter Norvig. 2020. Artificial Intelligence: A Modern Approach. 4ᵉ éd. Pearson. http://aima.cs.berkeley.edu/.

---

Marcel Turcotte

[email protected]

École de science informatique et de génie électrique (SIGE)

Université d’Ottawa