Introduction aux algorithmes de recherche

CSI 4106 - Automne 2024

Auteur·rice

Marcel Turcotte

Date de publication

Version: nov. 5, 2024 08h37

Préambule

Citation du jour

;document.getElementById("tweet-84569").innerHTML = tweet["html"];

Objectifs d’apprentissage

Comprendre le rôle des algorithmes de recherche en IA, essentiel pour la planification, le raisonnement, et des applications telles qu’AlphaGo.
Assimiler les concepts clés de la recherche : espace d’états, état initial/final, actions, modèles de transition, fonctions de coût.
Apprendre les différences et implémentations des algorithmes de recherche non-informés (BFS et DFS).
Implémenter et comparer BFS, DFS en utilisant le problème du puzzle à 8 cases.
Analyser la performance et l’optimalité de divers algorithmes de recherche.

L’objectif principal aujourd’hui est de fournir une justification, ainsi que d’introduire les concepts et la terminologie clés.

Justification

Pourquoi étudier ces algorithmes?

Silver et al. (2016)

Justification

Nous avons perfectionné notre expertise en apprentissage automatique au point de bien comprendre les réseaux neuronaux et le deep learning, ce qui nous permet de développer des modèles simples avec Keras.

. . .

En revanche, les récentes avancées sur les recherche arborescente de Monte-Carlo (MCTS) ont joué un rôle central dans la recherche en intelligence artificielle. Nous passons donc de la concentration sur le deep learning vers l’exploration de la recherche.

Justification

L’intégration du deep learning et de MCTS sous-tend des applications modernes comme AlphaGo, AlphaZero, et MuZero.

. . .

Les algorithmes de recherche sont donc cruciaux pour la planification et le raisonnement et leur importance devrait croître avec les avancées technologiques.

Recherche (un historique biaisé)

1968 – A* : Recherche heuristique pour la planification en IA.
1970s-1980s – Algorithmes à population (ex : algorithmes génétiques) : Optimisation stochastique pour grands espaces.
1980s – CSP (Problèmes de satisfaction de contraintes) : Recherche dans des espaces structurés avec contraintes explicites.
2013 – DQN : Apprentissage par renforcement (Q-learning) sur données brutes.
2015 – AlphaGo : Recherche d’arbres de jeu avec MCTS combiné au deep learning.
2017 – AlphaZero : MCTS pour auto-apprentissage dans plusieurs domaines.
2019 – MuZero : Recherche dans environnements inconnus sans modèles préexistants.
2020 – Agent57 : Recherche généralisée à travers divers environnements (jeux Atari).
2021 – FunSearch : Généralisation possible des techniques de recherche.

Recherche

L’ordinateur qui a maîtrisé le jeu de Go. Nature Video YouTube le 27-01-2016. (7m 52s)

En 1997, le Deep Blue d’IBM a vaincu le champion du monde d’échecs en titre, Garry Kasparov. Cependant, la communauté de l’IA n’a pas été particulièrement impressionnée, car le principal accomplissement du système résidait dans sa capacité à évaluer 200 millions de positions d’échecs par seconde. Après le match, Kasparov a remarqué que Deep Blue était “aussi intelligent que votre réveil.”

Depuis lors, des avancées significatives ont été réalisées. Contrairement à Deep Blue, AlphaZero s’appuie sur “des approches plus intéressantes que la recherche par force brute, qui sont peut-être plus humaines dans la façon dont elles traitent la position.” Cela a incité Kasparov à exprimer son approbation, déclarant : “Je ne peux pas cacher ma satisfaction que [AlphaZero] joue avec un style dynamique qui rappelle le mien !”

AlphaGo - Le Film

Oui, AlphaGo a réussi à battre le champion du monde, Lee Sedol. (1h 30m)

AlphaGo2MuZero

Attribution: MuZero : Maîtriser le Go, les échecs, le shogi et Atari sans règles, Google DeepMind, 23-12-2020. Schrittwieser et al. (2020)

David Silver, chercheur principal chez DeepMind et professeur à l’University College London, est l’un des principaux chercheurs sur ces projets. Il a obtenu son doctorat à l’Université de l’Alberta, où il a été supervisé par Richard Sutton.

Vous pourriez également vouloir regarder la vidéo suivante : AlphaGo Zero : Découvrir de nouvelles connaissances. Publiée sur YouTube le 18-10-2017.

Recherche

Applications

Cheminement et navigation : Utilisé en robotique et dans les jeux vidéo pour trouver un chemin d’un point de départ à une destination.
Résolution de puzzles : Résolution de problèmes comme le puzzle à 8 cases, labyrinthes, ou Sudoku.
Analyse de réseaux : Analyse de connectivité et des chemins les plus courts dans les réseaux sociaux ou les cartes de transport.
Jeux : Évaluation des coups dans les jeux comme les échecs ou le Go.

Applications

Planification et ordonnancement : Planification des tâches dans la gestion de projet ou l’ordonnancement de vols.
Allocation de ressources : Allocation de ressources dans un réseau ou organisation.
Problèmes de configuration : Assemblage de composants pour satisfaire des exigences, comme la configuration d’un système informatique.

Applications

Décisions sous incertitude : Décisions en jeux de stratégie en temps réel ou simulations.
Narration : Les modèles de langage peuvent générer des récits lorsqu’ils sont guidés par un plan valide provenant d’un planificateur automatisé. (Simon et Muise 2024)

Les applications des algorithmes de recherche sont à la fois nombreuses et diverses.

La recherche a été un domaine actif d’investigation non seulement en raison de sa large gamme d’applications, mais aussi en raison du potentiel d’améliorations des algorithmes pour réduire significativement le temps d’exécution des programmes ou faciliter l’exploration de plus grands espaces de recherche.

Plan

Recherche déterministe et heuristique : BFS, DFS, A* pour la recherche de chemins et l’optimisation en IA classique.
CSPs et algorithmes basés sur la population : Focus sur les problèmes structurés et la recherche stochastique.
Algorithmes de jeux adversariaux : Minimax, élagage alpha-bêta, MCTS pour la prise de décision dans des environnements compétitifs.

Ce cours et les suivants couvriront en détail ces sujets.

Définition

(Russell et Norvig 2020, 63)

Lorsqu’il n’est pas immédiatement évident de savoir quelle action correcte entreprendre, un agent peut avoir besoin de planifier à l’avance : considérer une séquence d’actions qui forment un chemin vers un état objectif. Un tel agent est appelé un agent de résolution de problèmes, et le processus computationnel qu’il entreprend est appelé recherche.

Terminologie

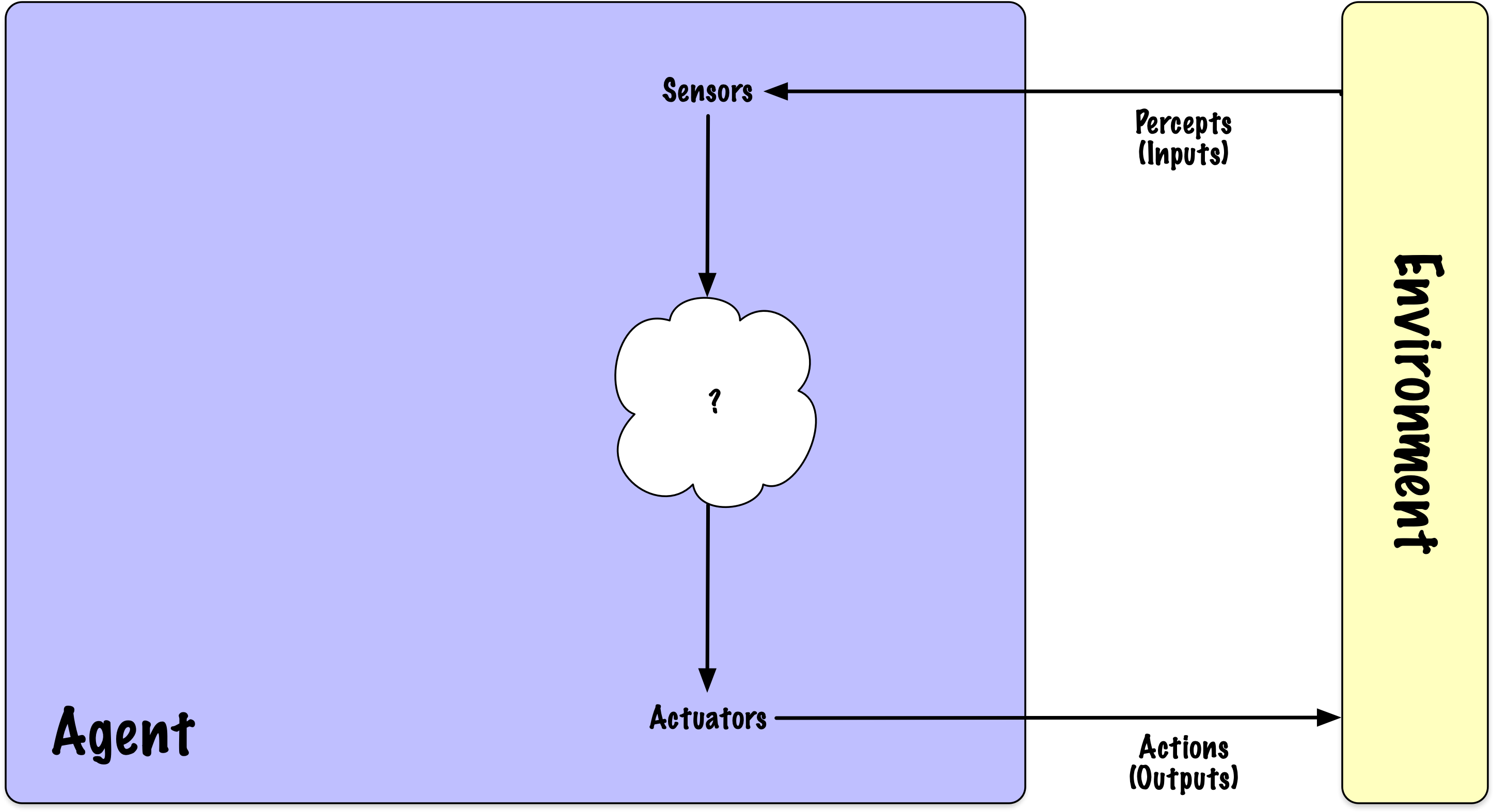
Un agent est une entité qui effectue des actions. Un agent rationnel est celui qui agit pour atteindre le “meilleur” résultat. Conceptuellement, un agent perçoit son environnement par le biais de capteurs et interagit avec celui-ci à l’aide d’actionneurs.

La définition d’un agent en intelligence artificielle (IA) partage certaines similitudes avec la définition psychologique, mais il existe des distinctions clés. En IA, un agent est une entité autonome qui perçoit son environnement grâce à des capteurs et agit sur celui-ci à l’aide d’actionneurs pour atteindre des objectifs spécifiques. Les deux définitions impliquent la perception, la prise de décision et l’action.

Cependant, alors que les agents psychologiques sont humains ou biologiques et impliquent des processus cognitifs et émotionnels complexes, les agents en IA sont computationnels et fonctionnent sur la base d’algorithmes conçus pour maximiser certaines mesures de performance ou atteindre des objectifs prédéfinis. L’accent en IA est davantage mis sur la mise en œuvre technique de ces processus, tandis qu’en psychologie, l’accent est mis sur la compréhension des aspects cognitifs et motivationnels de l’agence.

Le concept de conception agentique en ingénierie logicielle et en intelligence artificielle a connu une résurgence de popularité.

Caractéristiques de l’environnement

Observabilité : Partiellement observable ou totalement observable
Composition de l’agent : Agent unique ou multiple
Prédictibilité : Déterministe ou non déterministe
Dépendance d’état : Sans état ou avec état
Dynamique temporelle : Statique ou dynamique
Représentation de l’état : Discrète ou continue

Dans ce cours, les environnements sont supposés être : totalement observables, agent unique, sans état, déterministes, statiques et discrets.

Les caractéristiques d’un environnement influencent la complexité de la résolution de problèmes.

Un environnement totalement observable permet à l’agent de détecter tous les aspects pertinents pour la prise de décision.
Dans un environnement déterministe, l’agent peut prédire l’état suivant en fonction de l’état actuel et de son action subséquente.
Les environnements sans état (épisodiques) impliquent des décisions ou actions indépendantes des actions antérieures, avec des expériences divisées en épisodes non reliés. Un exemple est un problème de classification.
Les environnements avec état (séquentiels) nécessitent que le résultat de chaque action puisse affecter les décisions futures, car la séquence des actions impacte l’état et les choix ultérieurs. Un exemple est un jeu d’échecs.
Un environnement dynamique est caractérisé par des changements de contexte pendant que l’agent délibère.
Les échecs servent d’exemple d’environnement discret, avec un nombre fini, bien que grand, d’états. En revanche, un véhicule autonome fonctionne dans un environnement à état continu et temps continu.

Processus de résolution de problèmes

Recherche : Le processus implique de simuler des séquences d’actions jusqu’à ce que l’agent atteigne son objectif. Une séquence réussie est appelée une solution.

Une formulation précise facilite le développement de code réutilisable.

Un environnement caractérisé comme sans état, agent unique, totalement observable, déterministe, statique et discret implique que la solution à tout problème dans ce contexte est une séquence fixe d’actions.

Sans état : Chaque décision est indépendante des actions précédentes, ce qui signifie que la solution ne dépend pas de l’historique.
Agent unique : Il n’y a pas d’interaction avec d’autres agents qui pourrait introduire de la variabilité.
Totalement observable : L’agent dispose d’informations complètes sur l’environnement, permettant une prise de décision précise.
Déterministe : Le résultat des actions est prévisible, sans aléatoire affectant le résultat.
Statique : L’environnement ne change pas au fil du temps, les conditions restent donc constantes.
Discret : L’environnement a un nombre fini d’états et d’actions, permettant une séquence claire d’étapes.

Je suppose que vous êtes déjà familier avec ces concepts, et donc, ce cours initial sert principalement de révision.

Problème de recherche

Un ensemble d’états, appelé espace d’états.
Un état initial où l’agent commence.
Un ou plusieurs états objectifs qui définissent des résultats réussis.
Un ensemble d’actions disponibles dans un état donné \(s\).
Un modèle de transition qui détermine l’état suivant en fonction de l’état actuel et de l’action sélectionnée.
Une fonction de coût d’action qui spécifie le coût de l’exécution de l’action \(a\) dans l’état \(s\) pour atteindre l’état \(s'\).

Définitions

Un chemin est défini comme une séquence d’actions.
Une solution est un chemin qui relie l’état initial à l’état objectif.
Une solution optimale est le chemin avec le coût le plus bas parmi toutes les solutions possibles.

Nous supposons que le coût du chemin est la somme des coûts individuels des actions, et que tous les coûts sont positifs. L’espace d’états peut être conceptualisé comme un graphe, où les nœuds représentent les états et les arêtes correspondent aux actions.

Dans certains problèmes, plusieurs solutions optimales peuvent exister. Cependant, il est généralement suffisant d’identifier et de rapporter une seule solution optimale. Fournir toutes les solutions optimales peut considérablement augmenter la complexité en temps et en espace pour certains problèmes.

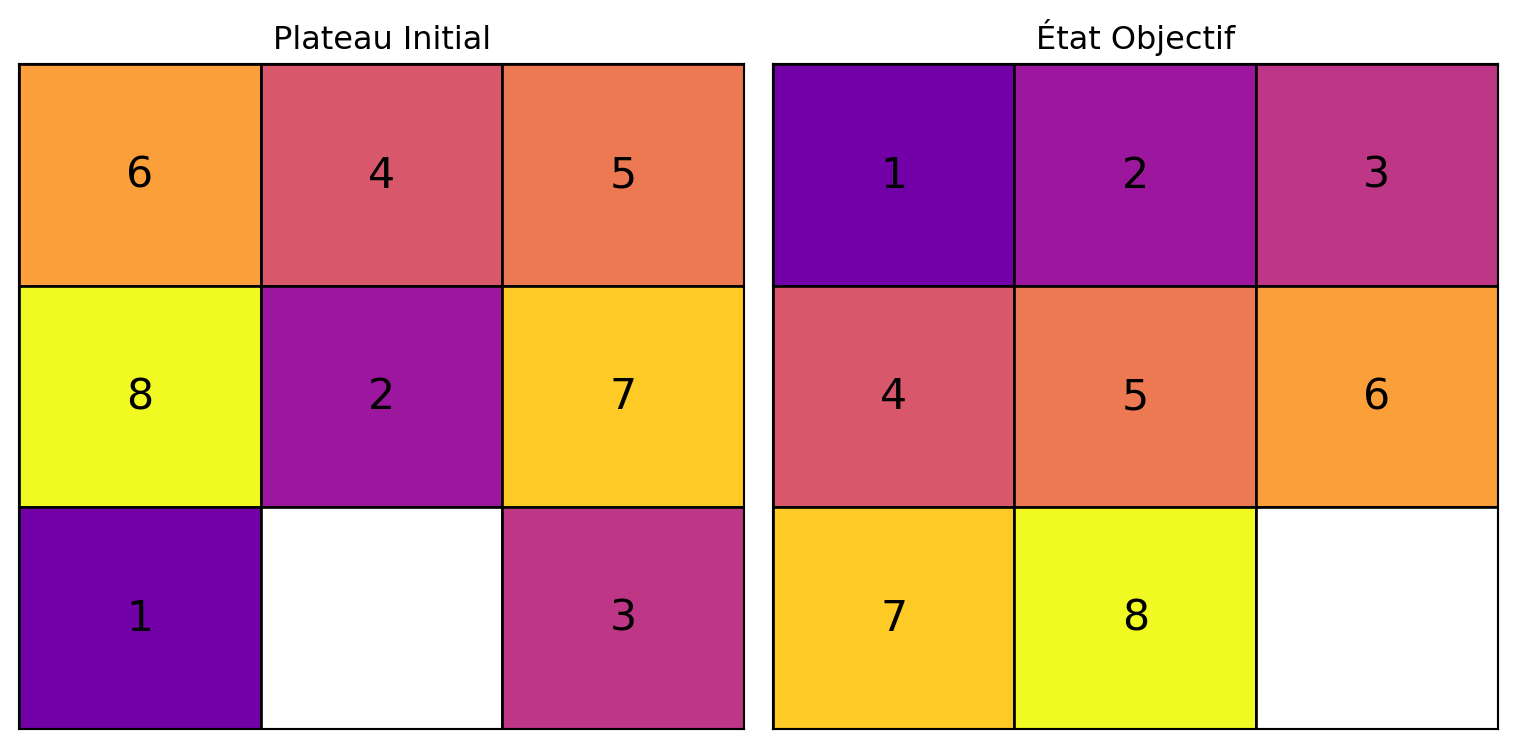
Exemple : 8-Puzzle

8-Puzzle

Comment les états peuvent-ils être représentés ?
Qu’est-ce qui constitue l’état initial ?
Qu’est-ce qui définit les actions ?
Qu’est-ce qui constituerait un chemin ?
Qu’est-ce qui caractérise l’état objectif ?
Qu’est-ce qui constituerait une solution ?
Quel devrait être le coût d’une action ?

Chaque état peut être représenté comme une liste contenant les chiffres de 0 à 8. Chaque chiffre correspond à une tuile, et sa position dans la liste reflète sa localisation dans la grille, avec 0 désignant l’espace vide.
L’état initial est une permutation des chiffres de 0 à 8.
Les actions incluent gauche, droite, haut et bas, qui impliquent de faire glisser une tuile adjacente dans l’espace vide.
Un chemin serait une séquence d’actions, par exemple gauche, gauche, haut.
Le modèle de transition associe un état donné et une action à un nouvel état. Toutes les actions ne sont pas réalisables à partir de chaque état ; par exemple, si l’espace vide est au bord de la grille, seules certaines actions sont possibles, comme bas, haut ou gauche.
L’état objectif est atteint lorsque la liste est ordonnée de 1 à 8, suivi de 0, indiquant que les tuiles sont correctement disposées. Combien y a-t-il d’états objectifs ?
Une solution serait un chemin valide transformant un état initial en un état objectif.
Chaque action entraîne un coût de 1.

Combien d’états possibles y a-t-il ?

Il y a 9! = 362 880 états. La force brute est envisageable.

Combien y a-t-il d’états pour le 15-Puzzle ?

15! = 1 307 674 368 000 (1,3 trillion) !

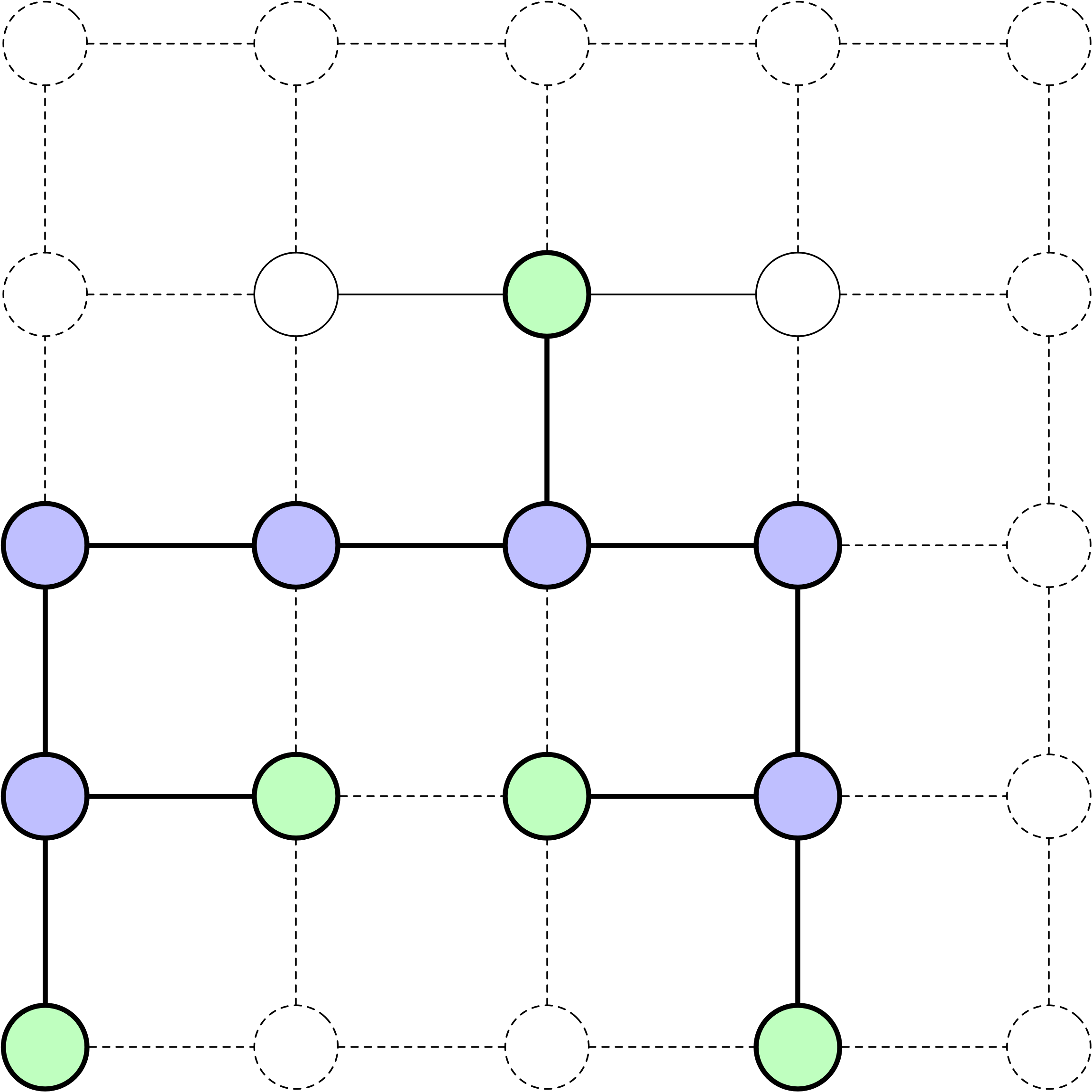
Arbre de recherche

Un arbre de recherche est une structure d’arbre conceptuelle où les nœuds représentent des états dans un espace d’états, et les arêtes représentent les actions possibles, facilitant l’exploration systématique pour trouver un chemin d’un état initial à un état objectif.

Les algorithmes de recherche que nous examinons aujourd’hui construisent un arbre de recherche, où chaque nœud représente un état au sein de l’espace d’états et chaque arête représente une action.

Il est important de distinguer entre l’arbre de recherche et l’espace d’états, qui peut être représenté comme un graphe. La structure de l’arbre de recherche varie en fonction de l’algorithme utilisé pour aborder le problème de recherche.

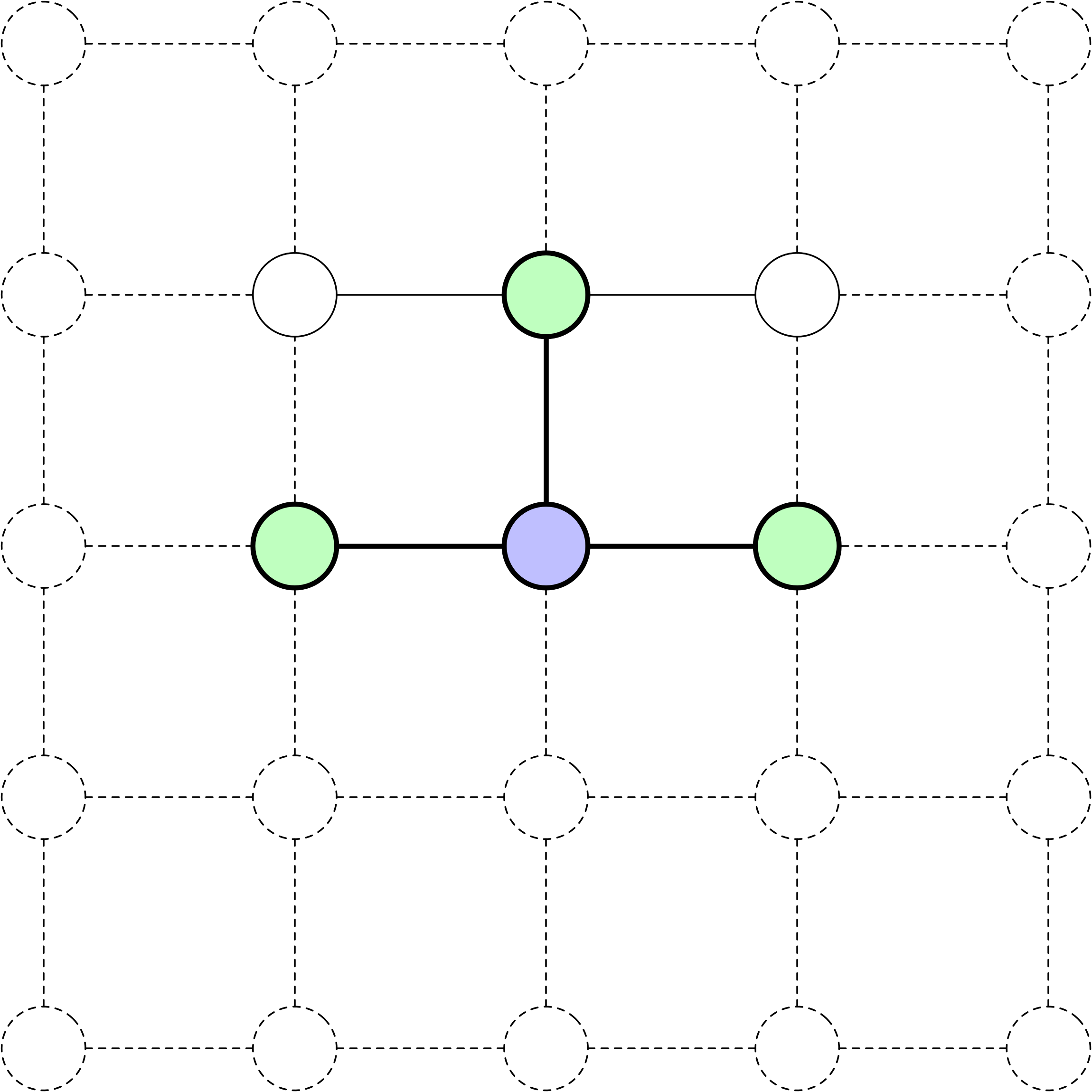
Arbre de recherche

Un exemple d’arbre de recherche pour le 8-Puzzle. La solution ici est incomplète.

Arbre de recherche

La racine de l’arbre de recherche représente l’état initial du problème.
Développer un nœud implique d’évaluer toutes les actions possibles disponibles à partir de cet état.
Le résultat d’une action est le nouvel état atteint après avoir appliqué cette action à l’état actuel.
À l’instar d’autres structures d’arbres, chaque nœud a un parent et peut avoir des enfants.

Une caractéristique distinctive d’un algorithme de recherche est sa méthode pour sélectionner le prochain nœud à développer.

Les nœuds racine et feuille sont des exceptions.

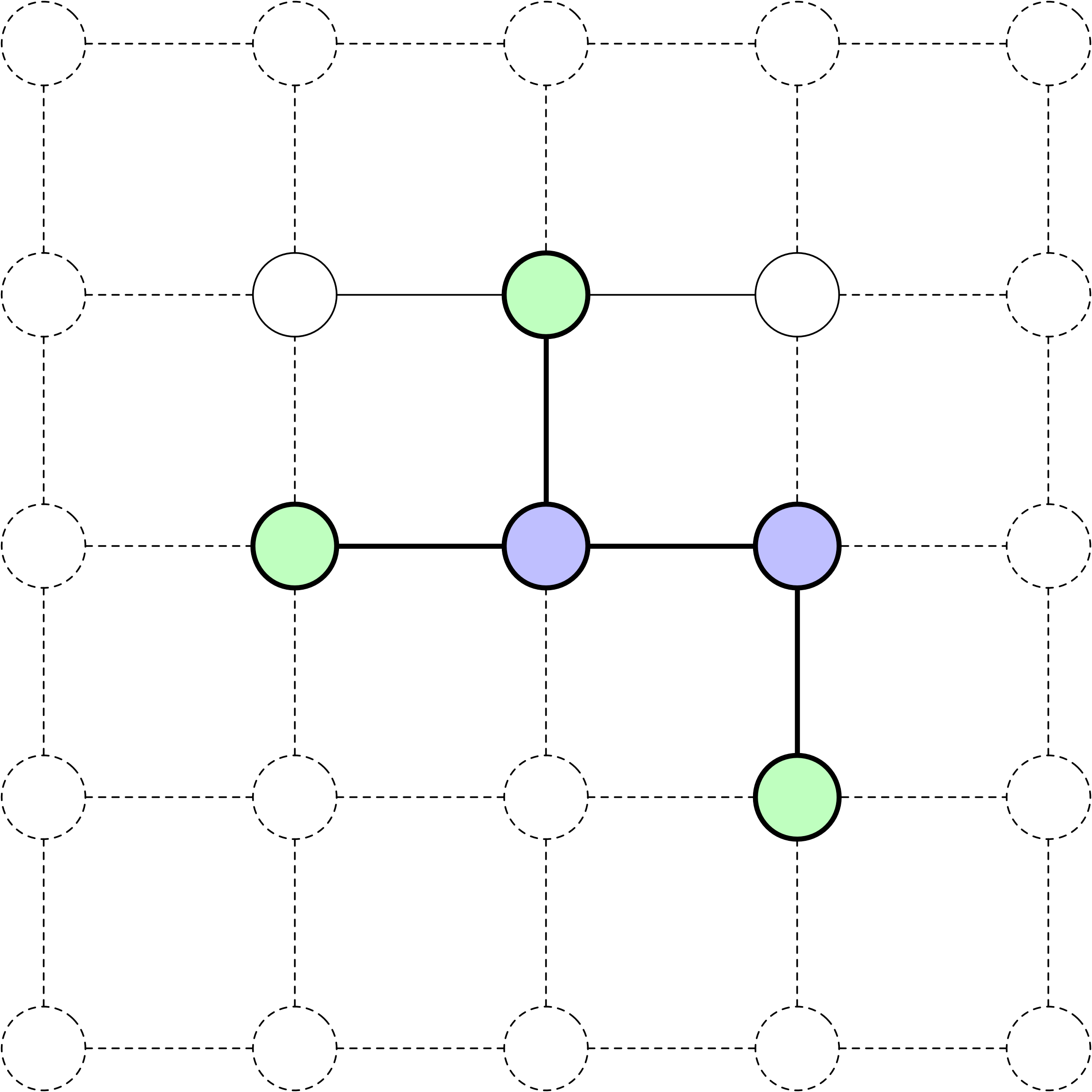
Frontière

Tout état correspondant à un nœud dans l’arbre de recherche est considéré comme atteint. Les nœuds de la frontière sont ceux qui ont été atteints mais n’ont pas encore été développés. Ci-dessus, il y a 10 nœuds développés et 11 nœuds de frontière, ce qui donne un total de 21 nœuds qui ont été atteints.

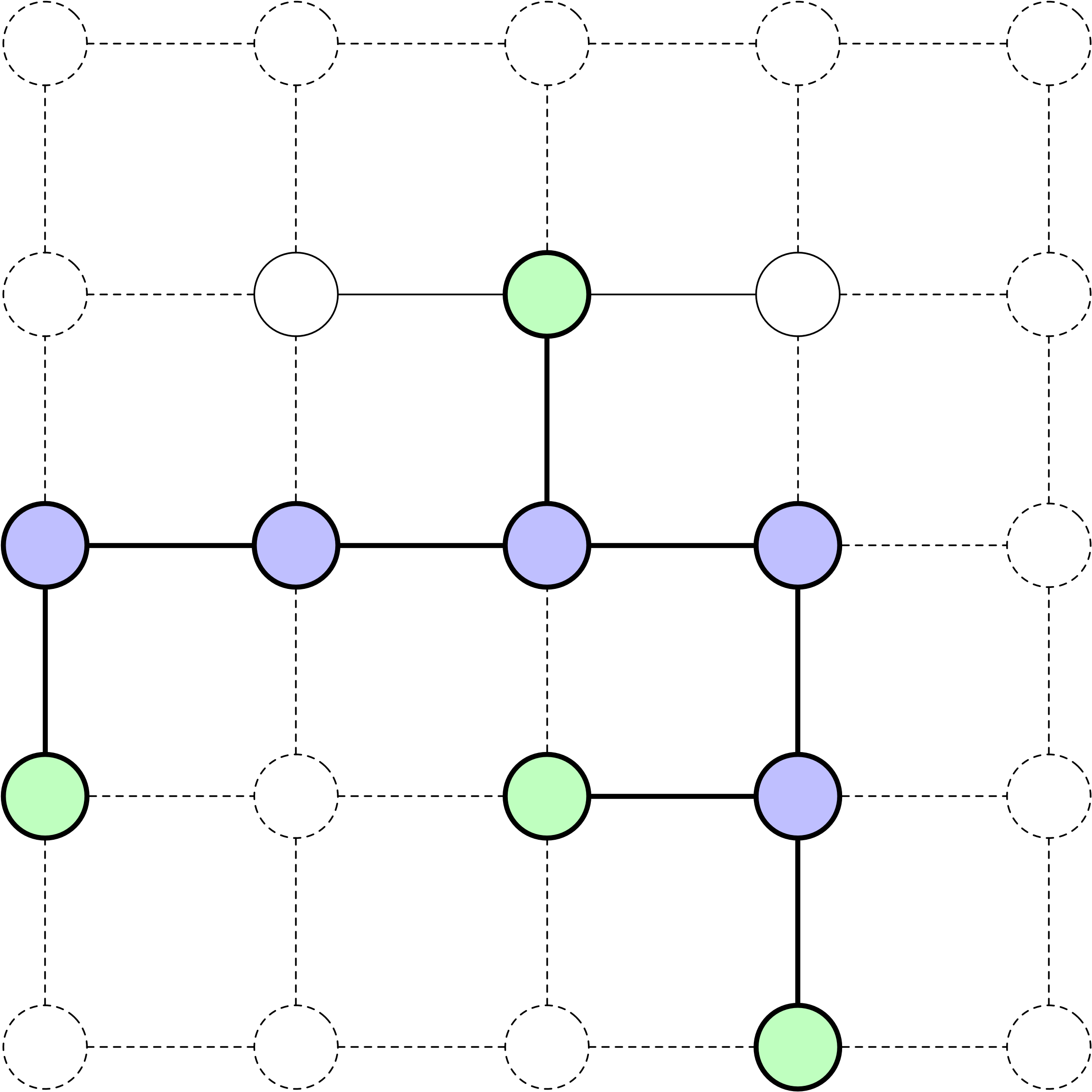
Frontière

Dans le 8-Puzzle, quatre actions sont possibles : glisser à gauche, à droite, vers le haut ou vers le bas. La recherche peut être visualisée sur une grille : nœuds violets : états développés, nœuds verts : états de la frontière (atteints mais non développés).

Les diagrammes correspondent à l’arbre de recherche présenté sur la page précédente. Par exemple, l’état initial peut être développé en utilisant trois actions : glisser à gauche, à droite et vers le haut. Le nœud (2, 3) ne peut être développé qu’en glissant vers le bas, tandis que le nœud (3, 3) peut être développé en glissant à gauche et vers le bas.

Frontière

Recherche non informée

Définition

Une recherche non informée est une stratégie de recherche qui explore l’espace de recherche en utilisant uniquement les informations disponibles dans la définition du problème, sans aucune connaissance spécifique au domaine, en évaluant les nœuds uniquement sur la base de leurs propriétés intrinsèques plutôt que sur des coûts estimés ou des heuristiques.

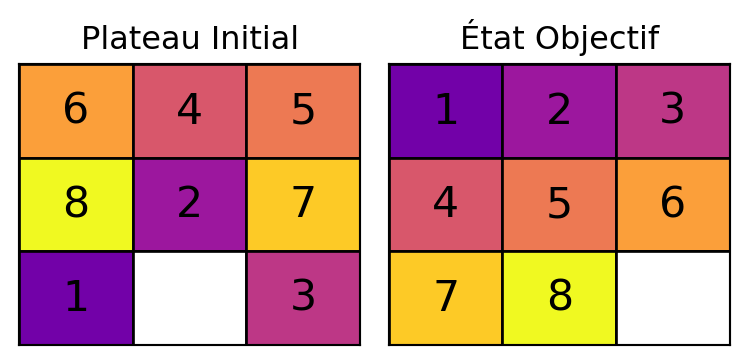
Représentation de l’état

initial_state_8 = [6, 4, 5,
                   8, 2, 7,
                   1, 0, 3]

goal_state_8 = [1, 2, 3,
                4, 5, 6,
                7, 8, 0]

Les états sont représentés comme des listes de chiffres. 0 représente la tuile vide.

`is_goal`

def is_goal(state, goal_state):
    """Détermine si un état donné correspond à l'état objectif."""
    return state == goal_state

Méthode auxiliaire.

`expand`

def expand(state):
    """Génère les états successeurs en déplaçant la tuile vide dans toutes les directions possibles."""
    size = int(len(state) ** 0.5) # Déterminer la taille du puzzle (3 pour le 8-Puzzle, 4 pour le 15-Puzzle)
    idx = state.index(0) # Trouver l'index de la tuile vide représentée par 0
    x, y = idx % size, idx // size # Convertir l'index en coordonnées (x, y)
    neighbors = []

    # Définir les mouvements possibles : Gauche, Droite, Haut, Bas
    moves = [(-1, 0), (1, 0), (0, -1), (0, 1)]
    for dx, dy in moves:
        nx, ny = x + dx, y + dy
        # Vérifier si la nouvelle position est dans les limites du puzzle
        if 0 <= nx < size and 0 <= ny < size:
            n_idx = ny * size + nx
            new_state = state.copy()
            # Échanger la tuile vide avec la tuile adjacente
            new_state[idx], new_state[n_idx] = new_state[n_idx], new_state[idx]
            neighbors.append(new_state)
    return neighbors

`expand`

expand(initial_state_8)

[[6, 4, 5, 8, 2, 7, 0, 1, 3],
 [6, 4, 5, 8, 2, 7, 1, 3, 0],
 [6, 4, 5, 8, 0, 7, 1, 2, 3]]

`is_empty`

def is_empty(frontier):
    """Vérifie si la frontière est vide."""
    return len(frontier) == 0

Si la frontière devient vide (plus de nœuds à développer), le problème n’a pas de solution.

Existe-t-il des plateaux de 8-Puzzle qui n’ont pas de solutions ?

La résolubilité du 8-Puzzle dépend du nombre d’inversions dans l’état initial. Une inversion est une paire de tuiles où une tuile avec un numéro plus élevé précède une tuile avec un numéro plus bas lorsque le puzzle est vu comme une séquence (en excluant la tuile vide).

`print_solution`

def print_solution(solution):
    """Affiche la séquence d'étapes de l'état initial à l'état objectif."""
    size = int(len(solution[0]) ** 0.5)
    for step, state in enumerate(solution):
        print(f"Étape {step} :")
        for i in range(size):
            row = state[i*size:(i+1)*size]
            print(' '.join(str(n) if n != 0 else ' ' for n in row))
        print()

Cycles

Un chemin qui revisite les mêmes états forme un cycle.

Permettre des cycles rendrait l’arbre de recherche résultant infini.

Pour éviter cela, nous surveillons les états qui ont été atteints, bien que cela entraîne un coût en mémoire.

Recherche en largeur

from collections import deque

La recherche en largeur (BFS) utilise une file d’attente pour gérer les nœuds de la frontière, également connus sous le nom de liste ouverte.

Recherche en largeur

def bfs(initial_state, goal_state):
    frontier = deque() # Initialiser la file d'attente pour BFS
    frontier.append((initial_state, [])) # Chaque élément est un tuple : (état, chemin)

    explored = set()
    explored.add(tuple(initial_state))

    iterations = 0 # utilisé simplement pour comparer les algorithmes

    while not is_empty(frontier):
        current_state, path = frontier.popleft()

        if is_goal(current_state, goal_state):
            print(f"Nombre d'itérations : {iterations}")
            return path + [current_state] # Retourner le chemin réussi

        iterations = iterations + 1

        for neighbor in expand(current_state):
            neighbor_tuple = tuple(neighbor)
            if neighbor_tuple not in explored:
                explored.add(neighbor_tuple)
                frontier.append((neighbor, path + [current_state]))

    return None # Aucune solution trouvée

Trouver le chemin le plus court de l’état initial à l’état objectif.

Cas simple

Nombre d'itérations : 12

initial_state_8 = [1, 2, 3,
                   4, 0, 6,
                   7, 5, 8]

goal_state_8 = [1, 2, 3,
                4, 5, 6,
                7, 8, 0]

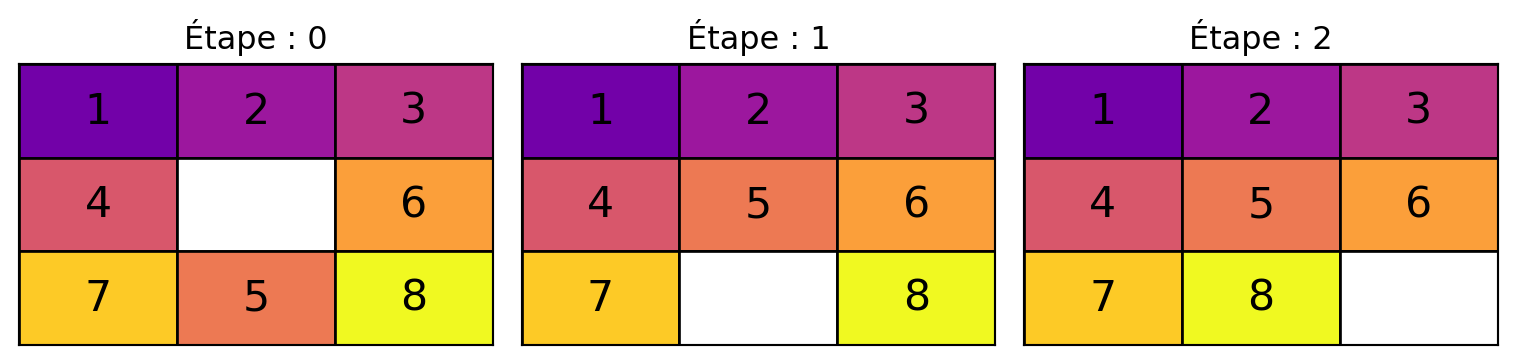
bfs(initial_state_8, goal_state_8)

Nombre d'itérations : 12

[[1, 2, 3, 4, 0, 6, 7, 5, 8],
 [1, 2, 3, 4, 5, 6, 7, 0, 8],
 [1, 2, 3, 4, 5, 6, 7, 8, 0]]

Cas difficile

initial_state_8 = [6, 4, 5,
                   8, 2, 7,
                   1, 0, 3]

goal_state_8 = [1, 2, 3,
                4, 5, 6,
                7, 8, 0]

print("Résolution du 8-Puzzle avec la recherche en largeur (BFS)...")

solution_8_bfs = bfs(initial_state_8, goal_state_8)

if solution_8_bfs:
    print(f"Solution BFS trouvée en {len(solution_8_bfs) - 1} mouvements :")
    print_solution(solution_8_bfs)
else:
    print("Aucune solution trouvée pour le 8-Puzzle en utilisant BFS.")

Résolution du 8-Puzzle avec la recherche en largeur (BFS)...
Nombre d'itérations : 145605
Solution BFS trouvée en 25 mouvements :
Étape 0 :
6 4 5
8 2 7
1   3

Étape 1 :
6 4 5
8 2 7
  1 3

Étape 2 :
6 4 5
  2 7
8 1 3

Étape 3 :
6 4 5
2   7
8 1 3

Étape 4 :
6   5
2 4 7
8 1 3

Étape 5 :
  6 5
2 4 7
8 1 3

Étape 6 :
2 6 5
  4 7
8 1 3

Étape 7 :
2 6 5
4   7
8 1 3

Étape 8 :
2 6 5
4 1 7
8   3

Étape 9 :
2 6 5
4 1 7
  8 3

Étape 10 :
2 6 5
  1 7
4 8 3

Étape 11 :
2 6 5
1   7
4 8 3

Étape 12 :
2 6 5
1 7  
4 8 3

Étape 13 :
2 6 5
1 7 3
4 8  

Étape 14 :
2 6 5
1 7 3
4   8

Étape 15 :
2 6 5
1   3
4 7 8

Étape 16 :
2   5
1 6 3
4 7 8

Étape 17 :
2 5  
1 6 3
4 7 8

Étape 18 :
2 5 3
1 6  
4 7 8

Étape 19 :
2 5 3
1   6
4 7 8

Étape 20 :
2   3
1 5 6
4 7 8

Étape 21 :
  2 3
1 5 6
4 7 8

Étape 22 :
1 2 3
  5 6
4 7 8

Étape 23 :
1 2 3
4 5 6
  7 8

Étape 24 :
1 2 3
4 5 6
7   8

Étape 25 :
1 2 3
4 5 6
7 8

Arbre de recherche BFS

L’arbre de recherche ci-dessus illustre les 20 premières itérations de la recherche en largeur (BFS) pour l’objectif initial spécifié.

Recherche en profondeur

def dfs(initial_state, goal_state):
    frontier = [(initial_state, [])] # Chaque élément est un tuple : (état, chemin)

    explored = set()
    explored.add(tuple(initial_state))

    iterations = 0

    while not is_empty(frontier):
        current_state, path = frontier.pop()

        if is_goal(current_state, goal_state):
            print(f"Nombre d'itérations : {iterations}")
            return path + [current_state] # Retourner le chemin réussi

        iterations = iterations + 1

        for neighbor in expand(current_state):
            neighbor_tuple = tuple(neighbor)
            if neighbor_tuple not in explored:
                explored.add(neighbor_tuple)
                frontier.append((neighbor, path + [current_state]))

    return None # Aucune solution trouvée

Quel est le comportement de la recherche en profondeur (DFS) ?

La recherche en profondeur (DFS) développe constamment le nœud le plus profond.

Quand le processus d’approfondissement s’arrête-t-il ?

Il cesse lorsque tous les nœuds enfants correspondent à des états déjà visités.

Que se passe-t-il ensuite ?

L’algorithme revient en arrière jusqu’au nœud le plus récent de la frontière.

Si tous les enfants de ce nœud correspondent également à des états déjà visités, l’algorithme continue de revenir en arrière.

Arbre de recherche DFS

Arbre de recherche DFS

Cas Simple

Nombre d'itérations : 2

initial_state_8 = [1, 2, 3,
                   4, 0, 6,
                   7, 5, 8]

goal_state_8 = [1, 2, 3,
                4, 5, 6,
                7, 8, 0]

bfs(initial_state_8, goal_state_8)

Nombre d'itérations : 12

[[1, 2, 3, 4, 0, 6, 7, 5, 8],
 [1, 2, 3, 4, 5, 6, 7, 0, 8],
 [1, 2, 3, 4, 5, 6, 7, 8, 0]]

Cas Difficile

initial_state_8 = [6, 4, 5,
                   8, 2, 7,
                   1, 0, 3]

goal_state_8 = [1, 2, 3,
                4, 5, 6,
                7, 8, 0]

print("Résolution du 8-Puzzle avec DFS...")

solution_8_bfs = dfs(initial_state_8, goal_state_8)

if solution_8_bfs:
    print(f"Solution DFS trouvée en {len(solution_8_bfs) - 1} mouvements :")
    print_solution(solution_8_bfs)
else:
    print("Aucune solution trouvée pour le 8-Puzzle en utilisant DFS.")

Résolution du 8-Puzzle avec DFS...
Nombre d'itérations : 1187
Solution DFS trouvée en 1157 mouvements :
Étape 0 :
6 4 5
8 2 7
1   3

Étape 1 :
6 4 5
8   7
1 2 3

Étape 2 :
6   5
8 4 7
1 2 3

Étape 3 :
6 5  
8 4 7
1 2 3

Étape 4 :
6 5 7
8 4  
1 2 3

Étape 5 :
6 5 7
8 4 3
1 2  

Étape 6 :
6 5 7
8 4 3
1   2

Étape 7 :
6 5 7
8   3
1 4 2

Étape 8 :
6   7
8 5 3
1 4 2

Étape 9 :
6 7  
8 5 3
1 4 2

Étape 10 :
6 7 3
8 5  
1 4 2

Étape 11 :
6 7 3
8 5 2
1 4  

Étape 12 :
6 7 3
8 5 2
1   4

Étape 13 :
6 7 3
8   2
1 5 4

Étape 14 :
6   3
8 7 2
1 5 4

Étape 15 :
6 3  
8 7 2
1 5 4

Étape 16 :
6 3 2
8 7  
1 5 4

Étape 17 :
6 3 2
8 7 4
1 5  

Étape 18 :
6 3 2
8 7 4
1   5

Étape 19 :
6 3 2
8   4
1 7 5

Étape 20 :
6   2
8 3 4
1 7 5

Étape 21 :
6 2  
8 3 4
1 7 5

Étape 22 :
6 2 4
8 3  
1 7 5

Étape 23 :
6 2 4
8 3 5
1 7  

Étape 24 :
6 2 4
8 3 5
1   7

Étape 25 :
6 2 4
8   5
1 3 7

Étape 26 :
6   4
8 2 5
1 3 7

Étape 27 :
6 4  
8 2 5
1 3 7

Étape 28 :
6 4 5
8 2  
1 3 7

Étape 29 :
6 4 5
8   2
1 3 7

Étape 30 :
6 4 5
8 3 2
1   7

Étape 31 :
6 4 5
8 3 2
1 7  

Étape 32 :
6 4 5
8 3  
1 7 2

Étape 33 :
6 4  
8 3 5
1 7 2

Étape 34 :
6   4
8 3 5
1 7 2

Étape 35 :
6 3 4
8   5
1 7 2

Étape 36 :
6 3 4
8 7 5
1   2

Étape 37 :
6 3 4
8 7 5
1 2  

Étape 38 :
6 3 4
8 7  
1 2 5

Étape 39 :
6 3  
8 7 4
1 2 5

Étape 40 :
6   3
8 7 4
1 2 5

Étape 41 :
6 7 3
8   4
1 2 5

Étape 42 :
6 7 3
8 2 4
1   5

Étape 43 :
6 7 3
8 2 4
  1 5

Étape 44 :
6 7 3
  2 4
8 1 5

Étape 45 :
  7 3
6 2 4
8 1 5

Étape 46 :
7   3
6 2 4
8 1 5

Étape 47 :
7 2 3
6   4
8 1 5

Étape 48 :
7 2 3
6 1 4
8   5

Étape 49 :
7 2 3
6 1 4
8 5  

Étape 50 :
7 2 3
6 1  
8 5 4

Étape 51 :
7 2  
6 1 3
8 5 4

Étape 52 :
7   2
6 1 3
8 5 4

Étape 53 :
7 1 2
6   3
8 5 4

Étape 54 :
7 1 2
6 5 3
8   4

Étape 55 :
7 1 2
6 5 3
8 4  

Étape 56 :
7 1 2
6 5  
8 4 3

Étape 57 :
7 1  
6 5 2
8 4 3

Étape 58 :
7   1
6 5 2
8 4 3

Étape 59 :
7 5 1
6   2
8 4 3

Étape 60 :
7 5 1
6 4 2
8   3

Étape 61 :
7 5 1
6 4 2
8 3  

Étape 62 :
7 5 1
6 4  
8 3 2

Étape 63 :
7 5  
6 4 1
8 3 2

Étape 64 :
7   5
6 4 1
8 3 2

Étape 65 :
7 4 5
6   1
8 3 2

Étape 66 :
7 4 5
6 3 1
8   2

Étape 67 :
7 4 5
6 3 1
8 2  

Étape 68 :
7 4 5
6 3  
8 2 1

Étape 69 :
7 4  
6 3 5
8 2 1

Étape 70 :
7   4
6 3 5
8 2 1

Étape 71 :
7 3 4
6   5
8 2 1

Étape 72 :
7 3 4
6 2 5
8   1

Étape 73 :
7 3 4
6 2 5
8 1  

Étape 74 :
7 3 4
6 2  
8 1 5

Étape 75 :
7 3 4
6   2
8 1 5

Étape 76 :
7 3 4
6 1 2
8   5

Étape 77 :
7 3 4
6 1 2
8 5  

Étape 78 :
7 3 4
6 1  
8 5 2

Étape 79 :
7 3  
6 1 4
8 5 2

Étape 80 :
7   3
6 1 4
8 5 2

Étape 81 :
7 1 3
6   4
8 5 2

Étape 82 :
7 1 3
6 5 4
8   2

Étape 83 :
7 1 3
6 5 4
8 2  

Étape 84 :
7 1 3
6 5  
8 2 4

Étape 85 :
7 1  
6 5 3
8 2 4

Étape 86 :
7   1
6 5 3
8 2 4

Étape 87 :
7 5 1
6   3
8 2 4

Étape 88 :
7 5 1
6 2 3
8   4

Étape 89 :
7 5 1
6 2 3
  8 4

Étape 90 :
7 5 1
  2 3
6 8 4

Étape 91 :
  5 1
7 2 3
6 8 4

Étape 92 :
5   1
7 2 3
6 8 4

Étape 93 :
5 2 1
7   3
6 8 4

Étape 94 :
5 2 1
7 8 3
6   4

Étape 95 :
5 2 1
7 8 3
6 4  

Étape 96 :
5 2 1
7 8  
6 4 3

Étape 97 :
5 2  
7 8 1
6 4 3

Étape 98 :
5   2
7 8 1
6 4 3

Étape 99 :
5 8 2
7   1
6 4 3

Étape 100 :
5 8 2
7 4 1
6   3

Étape 101 :
5 8 2
7 4 1
6 3  

Étape 102 :
5 8 2
7 4  
6 3 1

Étape 103 :
5 8  
7 4 2
6 3 1

Étape 104 :
5   8
7 4 2
6 3 1

Étape 105 :
5 4 8
7   2
6 3 1

Étape 106 :
5 4 8
7 3 2
6   1

Étape 107 :
5 4 8
7 3 2
6 1  

Étape 108 :
5 4 8
7 3  
6 1 2

Étape 109 :
5 4  
7 3 8
6 1 2

Étape 110 :
5   4
7 3 8
6 1 2

Étape 111 :
5 3 4
7   8
6 1 2

Étape 112 :
5 3 4
7 1 8
6   2

Étape 113 :
5 3 4
7 1 8
6 2  

Étape 114 :
5 3 4
7 1  
6 2 8

Étape 115 :
5 3  
7 1 4
6 2 8

Étape 116 :
5   3
7 1 4
6 2 8

Étape 117 :
5 1 3
7   4
6 2 8

Étape 118 :
5 1 3
7 2 4
6   8

Étape 119 :
5 1 3
7 2 4
6 8  

Étape 120 :
5 1 3
7 2  
6 8 4

Étape 121 :
5 1 3
7   2
6 8 4

Étape 122 :
5 1 3
7 8 2
6   4

Étape 123 :
5 1 3
7 8 2
6 4  

Étape 124 :
5 1 3
7 8  
6 4 2

Étape 125 :
5 1  
7 8 3
6 4 2

Étape 126 :
5   1
7 8 3
6 4 2

Étape 127 :
5 8 1
7   3
6 4 2

Étape 128 :
5 8 1
7 4 3
6   2

Étape 129 :
5 8 1
7 4 3
6 2  

Étape 130 :
5 8 1
7 4  
6 2 3

Étape 131 :
5 8  
7 4 1
6 2 3

Étape 132 :
5   8
7 4 1
6 2 3

Étape 133 :
5 4 8
7   1
6 2 3

Étape 134 :
5 4 8
7 2 1
6   3

Étape 135 :
5 4 8
7 2 1
  6 3

Étape 136 :
5 4 8
  2 1
7 6 3

Étape 137 :
  4 8
5 2 1
7 6 3

Étape 138 :
4   8
5 2 1
7 6 3

Étape 139 :
4 2 8
5   1
7 6 3

Étape 140 :
4 2 8
5 6 1
7   3

Étape 141 :
4 2 8
5 6 1
7 3  

Étape 142 :
4 2 8
5 6  
7 3 1

Étape 143 :
4 2  
5 6 8
7 3 1

Étape 144 :
4   2
5 6 8
7 3 1

Étape 145 :
4 6 2
5   8
7 3 1

Étape 146 :
4 6 2
5 3 8
7   1

Étape 147 :
4 6 2
5 3 8
7 1  

Étape 148 :
4 6 2
5 3  
7 1 8

Étape 149 :
4 6  
5 3 2
7 1 8

Étape 150 :
4   6
5 3 2
7 1 8

Étape 151 :
4 3 6
5   2
7 1 8

Étape 152 :
4 3 6
5 1 2
7   8

Étape 153 :
4 3 6
5 1 2
7 8  

Étape 154 :
4 3 6
5 1  
7 8 2

Étape 155 :
4 3  
5 1 6
7 8 2

Étape 156 :
4   3
5 1 6
7 8 2

Étape 157 :
4 1 3
5   6
7 8 2

Étape 158 :
4 1 3
5 8 6
7   2

Étape 159 :
4 1 3
5 8 6
7 2  

Étape 160 :
4 1 3
5 8  
7 2 6

Étape 161 :
4 1  
5 8 3
7 2 6

Étape 162 :
4   1
5 8 3
7 2 6

Étape 163 :
4 8 1
5   3
7 2 6

Étape 164 :
4 8 1
5 2 3
7   6

Étape 165 :
4 8 1
5 2 3
7 6  

Étape 166 :
4 8 1
5 2  
7 6 3

Étape 167 :
4 8 1
5   2
7 6 3

Étape 168 :
4 8 1
5 6 2
7   3

Étape 169 :
4 8 1
5 6 2
7 3  

Étape 170 :
4 8 1
5 6  
7 3 2

Étape 171 :
4 8  
5 6 1
7 3 2

Étape 172 :
4   8
5 6 1
7 3 2

Étape 173 :
4 6 8
5   1
7 3 2

Étape 174 :
4 6 8
5 3 1
7   2

Étape 175 :
4 6 8
5 3 1
7 2  

Étape 176 :
4 6 8
5 3  
7 2 1

Étape 177 :
4 6  
5 3 8
7 2 1

Étape 178 :
4   6
5 3 8
7 2 1

Étape 179 :
4 3 6
5   8
7 2 1

Étape 180 :
4 3 6
5 2 8
7   1

Étape 181 :
4 3 6
5 2 8
  7 1

Étape 182 :
4 3 6
  2 8
5 7 1

Étape 183 :
  3 6
4 2 8
5 7 1

Étape 184 :
3   6
4 2 8
5 7 1

Étape 185 :
3 2 6
4   8
5 7 1

Étape 186 :
3 2 6
4 7 8
5   1

Étape 187 :
3 2 6
4 7 8
5 1  

Étape 188 :
3 2 6
4 7  
5 1 8

Étape 189 :
3 2  
4 7 6
5 1 8

Étape 190 :
3   2
4 7 6
5 1 8

Étape 191 :
3 7 2
4   6
5 1 8

Étape 192 :
3 7 2
4 1 6
5   8

Étape 193 :
3 7 2
4 1 6
5 8  

Étape 194 :
3 7 2
4 1  
5 8 6

Étape 195 :
3 7  
4 1 2
5 8 6

Étape 196 :
3   7
4 1 2
5 8 6

Étape 197 :
3 1 7
4   2
5 8 6

Étape 198 :
3 1 7
4 8 2
5   6

Étape 199 :
3 1 7
4 8 2
5 6  

Étape 200 :
3 1 7
4 8  
5 6 2

Étape 201 :
3 1  
4 8 7
5 6 2

Étape 202 :
3   1
4 8 7
5 6 2

Étape 203 :
3 8 1
4   7
5 6 2

Étape 204 :
3 8 1
4 6 7
5   2

Étape 205 :
3 8 1
4 6 7
5 2  

Étape 206 :
3 8 1
4 6  
5 2 7

Étape 207 :
3 8  
4 6 1
5 2 7

Étape 208 :
3   8
4 6 1
5 2 7

Étape 209 :
3 6 8
4   1
5 2 7

Étape 210 :
3 6 8
4 2 1
5   7

Étape 211 :
3 6 8
4 2 1
5 7  

Étape 212 :
3 6 8
4 2  
5 7 1

Étape 213 :
3 6 8
4   2
5 7 1

Étape 214 :
3 6 8
4 7 2
5   1

Étape 215 :
3 6 8
4 7 2
5 1  

Étape 216 :
3 6 8
4 7  
5 1 2

Étape 217 :
3 6  
4 7 8
5 1 2

Étape 218 :
3   6
4 7 8
5 1 2

Étape 219 :
3 7 6
4   8
5 1 2

Étape 220 :
3 7 6
4 1 8
5   2

Étape 221 :
3 7 6
4 1 8
5 2  

Étape 222 :
3 7 6
4 1  
5 2 8

Étape 223 :
3 7  
4 1 6
5 2 8

Étape 224 :
3   7
4 1 6
5 2 8

Étape 225 :
3 1 7
4   6
5 2 8

Étape 226 :
3 1 7
4 2 6
5   8

Étape 227 :
3 1 7
4 2 6
  5 8

Étape 228 :
3 1 7
  2 6
4 5 8

Étape 229 :
  1 7
3 2 6
4 5 8

Étape 230 :
1   7
3 2 6
4 5 8

Étape 231 :
1 2 7
3   6
4 5 8

Étape 232 :
1 2 7
3 5 6
4   8

Étape 233 :
1 2 7
3 5 6
4 8  

Étape 234 :
1 2 7
3 5  
4 8 6

Étape 235 :
1 2  
3 5 7
4 8 6

Étape 236 :
1   2
3 5 7
4 8 6

Étape 237 :
1 5 2
3   7
4 8 6

Étape 238 :
1 5 2
3 8 7
4   6

Étape 239 :
1 5 2
3 8 7
4 6  

Étape 240 :
1 5 2
3 8  
4 6 7

Étape 241 :
1 5  
3 8 2
4 6 7

Étape 242 :
1   5
3 8 2
4 6 7

Étape 243 :
1 8 5
3   2
4 6 7

Étape 244 :
1 8 5
3 6 2
4   7

Étape 245 :
1 8 5
3 6 2
4 7  

Étape 246 :
1 8 5
3 6  
4 7 2

Étape 247 :
1 8  
3 6 5
4 7 2

Étape 248 :
1   8
3 6 5
4 7 2

Étape 249 :
1 6 8
3   5
4 7 2

Étape 250 :
1 6 8
3 7 5
4   2

Étape 251 :
1 6 8
3 7 5
4 2  

Étape 252 :
1 6 8
3 7  
4 2 5

Étape 253 :
1 6  
3 7 8
4 2 5

Étape 254 :
1   6
3 7 8
4 2 5

Étape 255 :
1 7 6
3   8
4 2 5

Étape 256 :
1 7 6
3 2 8
4   5

Étape 257 :
1 7 6
3 2 8
4 5  

Étape 258 :
1 7 6
3 2  
4 5 8

Étape 259 :
1 7 6
3   2
4 5 8

Étape 260 :
1 7 6
3 5 2
4   8

Étape 261 :
1 7 6
3 5 2
4 8  

Étape 262 :
1 7 6
3 5  
4 8 2

Étape 263 :
1 7  
3 5 6
4 8 2

Étape 264 :
1   7
3 5 6
4 8 2

Étape 265 :
1 5 7
3   6
4 8 2

Étape 266 :
1 5 7
3 8 6
4   2

Étape 267 :
1 5 7
3 8 6
4 2  

Étape 268 :
1 5 7
3 8  
4 2 6

Étape 269 :
1 5  
3 8 7
4 2 6

Étape 270 :
1   5
3 8 7
4 2 6

Étape 271 :
1 8 5
3   7
4 2 6

Étape 272 :
1 8 5
3 2 7
4   6

Étape 273 :
1 8 5
3 2 7
  4 6

Étape 274 :
1 8 5
  2 7
3 4 6

Étape 275 :
  8 5
1 2 7
3 4 6

Étape 276 :
8   5
1 2 7
3 4 6

Étape 277 :
8 2 5
1   7
3 4 6

Étape 278 :
8 2 5
1 4 7
3   6

Étape 279 :
8 2 5
1 4 7
3 6  

Étape 280 :
8 2 5
1 4  
3 6 7

Étape 281 :
8 2  
1 4 5
3 6 7

Étape 282 :
8   2
1 4 5
3 6 7

Étape 283 :
8 4 2
1   5
3 6 7

Étape 284 :
8 4 2
1 6 5
3   7

Étape 285 :
8 4 2
1 6 5
3 7  

Étape 286 :
8 4 2
1 6  
3 7 5

Étape 287 :
8 4  
1 6 2
3 7 5

Étape 288 :
8   4
1 6 2
3 7 5

Étape 289 :
8 6 4
1   2
3 7 5

Étape 290 :
8 6 4
1 7 2
3   5

Étape 291 :
8 6 4
1 7 2
3 5  

Étape 292 :
8 6 4
1 7  
3 5 2

Étape 293 :
8 6  
1 7 4
3 5 2

Étape 294 :
8   6
1 7 4
3 5 2

Étape 295 :
8 7 6
1   4
3 5 2

Étape 296 :
8 7 6
1 5 4
3   2

Étape 297 :
8 7 6
1 5 4
3 2  

Étape 298 :
8 7 6
1 5  
3 2 4

Étape 299 :
8 7  
1 5 6
3 2 4

Étape 300 :
8   7
1 5 6
3 2 4

Étape 301 :
8 5 7
1   6
3 2 4

Étape 302 :
8 5 7
1 2 6
3   4

Étape 303 :
8 5 7
1 2 6
3 4  

Étape 304 :
8 5 7
1 2  
3 4 6

Étape 305 :
8 5 7
1   2
3 4 6

Étape 306 :
8 5 7
1 4 2
3   6

Étape 307 :
8 5 7
1 4 2
3 6  

Étape 308 :
8 5 7
1 4  
3 6 2

Étape 309 :
8 5  
1 4 7
3 6 2

Étape 310 :
8   5
1 4 7
3 6 2

Étape 311 :
8 4 5
1   7
3 6 2

Étape 312 :
8 4 5
1 6 7
3   2

Étape 313 :
8 4 5
1 6 7
3 2  

Étape 314 :
8 4 5
1 6  
3 2 7

Étape 315 :
8 4  
1 6 5
3 2 7

Étape 316 :
8   4
1 6 5
3 2 7

Étape 317 :
8 6 4
1   5
3 2 7

Étape 318 :
8 6 4
1 2 5
3   7

Étape 319 :
8 6 4
1 2 5
  3 7

Étape 320 :
8 6 4
  2 5
1 3 7

Étape 321 :
8 6 4
2   5
1 3 7

Étape 322 :
8 6 4
2 3 5
1   7

Étape 323 :
8 6 4
2 3 5
1 7  

Étape 324 :
8 6 4
2 3  
1 7 5

Étape 325 :
8 6  
2 3 4
1 7 5

Étape 326 :
8   6
2 3 4
1 7 5

Étape 327 :
8 3 6
2   4
1 7 5

Étape 328 :
8 3 6
2 7 4
1   5

Étape 329 :
8 3 6
2 7 4
1 5  

Étape 330 :
8 3 6
2 7  
1 5 4

Étape 331 :
8 3  
2 7 6
1 5 4

Étape 332 :
8   3
2 7 6
1 5 4

Étape 333 :
8 7 3
2   6
1 5 4

Étape 334 :
8 7 3
2 5 6
1   4

Étape 335 :
8 7 3
2 5 6
1 4  

Étape 336 :
8 7 3
2 5  
1 4 6

Étape 337 :
8 7  
2 5 3
1 4 6

Étape 338 :
8   7
2 5 3
1 4 6

Étape 339 :
8 5 7
2   3
1 4 6

Étape 340 :
8 5 7
2 4 3
1   6

Étape 341 :
8 5 7
2 4 3
1 6  

Étape 342 :
8 5 7
2 4  
1 6 3

Étape 343 :
8 5  
2 4 7
1 6 3

Étape 344 :
8   5
2 4 7
1 6 3

Étape 345 :
8 4 5
2   7
1 6 3

Étape 346 :
8 4 5
2 6 7
1   3

Étape 347 :
8 4 5
2 6 7
1 3  

Étape 348 :
8 4 5
2 6  
1 3 7

Étape 349 :
8 4 5
2   6
1 3 7

Étape 350 :
8 4 5
2 3 6
1   7

Étape 351 :
8 4 5
2 3 6
1 7  

Étape 352 :
8 4 5
2 3  
1 7 6

Étape 353 :
8 4  
2 3 5
1 7 6

Étape 354 :
8   4
2 3 5
1 7 6

Étape 355 :
8 3 4
2   5
1 7 6

Étape 356 :
8 3 4
2 7 5
1   6

Étape 357 :
8 3 4
2 7 5
1 6  

Étape 358 :
8 3 4
2 7  
1 6 5

Étape 359 :
8 3  
2 7 4
1 6 5

Étape 360 :
8   3
2 7 4
1 6 5

Étape 361 :
8 7 3
2   4
1 6 5

Étape 362 :
8 7 3
2 6 4
1   5

Étape 363 :
8 7 3
2 6 4
  1 5

Étape 364 :
8 7 3
  6 4
2 1 5

Étape 365 :
  7 3
8 6 4
2 1 5

Étape 366 :
7   3
8 6 4
2 1 5

Étape 367 :
7 6 3
8   4
2 1 5

Étape 368 :
7 6 3
8 1 4
2   5

Étape 369 :
7 6 3
8 1 4
2 5  

Étape 370 :
7 6 3
8 1  
2 5 4

Étape 371 :
7 6  
8 1 3
2 5 4

Étape 372 :
7   6
8 1 3
2 5 4

Étape 373 :
7 1 6
8   3
2 5 4

Étape 374 :
7 1 6
8 5 3
2   4

Étape 375 :
7 1 6
8 5 3
2 4  

Étape 376 :
7 1 6
8 5  
2 4 3

Étape 377 :
7 1  
8 5 6
2 4 3

Étape 378 :
7   1
8 5 6
2 4 3

Étape 379 :
7 5 1
8   6
2 4 3

Étape 380 :
7 5 1
8 4 6
2   3

Étape 381 :
7 5 1
8 4 6
2 3  

Étape 382 :
7 5 1
8 4  
2 3 6

Étape 383 :
7 5  
8 4 1
2 3 6

Étape 384 :
7   5
8 4 1
2 3 6

Étape 385 :
7 4 5
8   1
2 3 6

Étape 386 :
7 4 5
8 3 1
2   6

Étape 387 :
7 4 5
8 3 1
2 6  

Étape 388 :
7 4 5
8 3  
2 6 1

Étape 389 :
7 4  
8 3 5
2 6 1

Étape 390 :
7   4
8 3 5
2 6 1

Étape 391 :
7 3 4
8   5
2 6 1

Étape 392 :
7 3 4
8 6 5
2   1

Étape 393 :
7 3 4
8 6 5
2 1  

Étape 394 :
7 3 4
8 6  
2 1 5

Étape 395 :
7 3 4
8   6
2 1 5

Étape 396 :
7 3 4
8 1 6
2   5

Étape 397 :
7 3 4
8 1 6
2 5  

Étape 398 :
7 3 4
8 1  
2 5 6

Étape 399 :
7 3  
8 1 4
2 5 6

Étape 400 :
7   3
8 1 4
2 5 6

Étape 401 :
7 1 3
8   4
2 5 6

Étape 402 :
7 1 3
8 5 4
2   6

Étape 403 :
7 1 3
8 5 4
2 6  

Étape 404 :
7 1 3
8 5  
2 6 4

Étape 405 :
7 1  
8 5 3
2 6 4

Étape 406 :
7   1
8 5 3
2 6 4

Étape 407 :
7 5 1
8   3
2 6 4

Étape 408 :
7 5 1
8 3  
2 6 4

Étape 409 :
7 5 1
8 3 4
2 6  

Étape 410 :
7 5 1
8 3 4
2   6

Étape 411 :
7 5 1
8 3 4
  2 6

Étape 412 :
7 5 1
  3 4
8 2 6

Étape 413 :
  5 1
7 3 4
8 2 6

Étape 414 :
5   1
7 3 4
8 2 6

Étape 415 :
5 3 1
7   4
8 2 6

Étape 416 :
5 3 1
7 2 4
8   6

Étape 417 :
5 3 1
7 2 4
8 6  

Étape 418 :
5 3 1
7 2  
8 6 4

Étape 419 :
5 3  
7 2 1
8 6 4

Étape 420 :
5   3
7 2 1
8 6 4

Étape 421 :
5 2 3
7   1
8 6 4

Étape 422 :
5 2 3
7 6 1
8   4

Étape 423 :
5 2 3
7 6 1
8 4  

Étape 424 :
5 2 3
7 6  
8 4 1

Étape 425 :
5 2  
7 6 3
8 4 1

Étape 426 :
5   2
7 6 3
8 4 1

Étape 427 :
5 6 2
7   3
8 4 1

Étape 428 :
5 6 2
7 4 3
8   1

Étape 429 :
5 6 2
7 4 3
8 1  

Étape 430 :
5 6 2
7 4  
8 1 3

Étape 431 :
5 6  
7 4 2
8 1 3

Étape 432 :
5   6
7 4 2
8 1 3

Étape 433 :
5 4 6
7   2
8 1 3

Étape 434 :
5 4 6
7 1 2
8   3

Étape 435 :
5 4 6
7 1 2
8 3  

Étape 436 :
5 4 6
7 1  
8 3 2

Étape 437 :
5 4  
7 1 6
8 3 2

Étape 438 :
5   4
7 1 6
8 3 2

Étape 439 :
5 1 4
7   6
8 3 2

Étape 440 :
5 1 4
7 3 6
8   2

Étape 441 :
5 1 4
7 3 6
8 2  

Étape 442 :
5 1 4
7 3  
8 2 6

Étape 443 :
5 1 4
7   3
8 2 6

Étape 444 :
5 1 4
7 2 3
8   6

Étape 445 :
5 1 4
7 2 3
8 6  

Étape 446 :
5 1 4
7 2  
8 6 3

Étape 447 :
5 1  
7 2 4
8 6 3

Étape 448 :
5   1
7 2 4
8 6 3

Étape 449 :
5 2 1
7   4
8 6 3

Étape 450 :
5 2 1
7 6 4
8   3

Étape 451 :
5 2 1
7 6 4
8 3  

Étape 452 :
5 2 1
7 6  
8 3 4

Étape 453 :
5 2  
7 6 1
8 3 4

Étape 454 :
5   2
7 6 1
8 3 4

Étape 455 :
5 6 2
7   1
8 3 4

Étape 456 :
5 6 2
7 3 1
8   4

Étape 457 :
5 6 2
7 3 1
  8 4

Étape 458 :
5 6 2
  3 1
7 8 4

Étape 459 :
  6 2
5 3 1
7 8 4

Étape 460 :
6   2
5 3 1
7 8 4

Étape 461 :
6 3 2
5   1
7 8 4

Étape 462 :
6 3 2
5 8 1
7   4

Étape 463 :
6 3 2
5 8 1
7 4  

Étape 464 :
6 3 2
5 8  
7 4 1

Étape 465 :
6 3  
5 8 2
7 4 1

Étape 466 :
6   3
5 8 2
7 4 1

Étape 467 :
6 8 3
5   2
7 4 1

Étape 468 :
6 8 3
5 4 2
7   1

Étape 469 :
6 8 3
5 4 2
7 1  

Étape 470 :
6 8 3
5 4  
7 1 2

Étape 471 :
6 8  
5 4 3
7 1 2

Étape 472 :
6   8
5 4 3
7 1 2

Étape 473 :
6 4 8
5   3
7 1 2

Étape 474 :
6 4 8
5 1 3
7   2

Étape 475 :
6 4 8
5 1 3
7 2  

Étape 476 :
6 4 8
5 1  
7 2 3

Étape 477 :
6 4  
5 1 8
7 2 3

Étape 478 :
6   4
5 1 8
7 2 3

Étape 479 :
6 1 4
5   8
7 2 3

Étape 480 :
6 1 4
5 2 8
7   3

Étape 481 :
6 1 4
5 2 8
7 3  

Étape 482 :
6 1 4
5 2  
7 3 8

Étape 483 :
6 1  
5 2 4
7 3 8

Étape 484 :
6   1
5 2 4
7 3 8

Étape 485 :
6 2 1
5   4
7 3 8

Étape 486 :
6 2 1
5 3 4
7   8

Étape 487 :
6 2 1
5 3 4
7 8  

Étape 488 :
6 2 1
5 3  
7 8 4

Étape 489 :
6 2 1
5   3
7 8 4

Étape 490 :
6 2 1
5 8 3
7   4

Étape 491 :
6 2 1
5 8 3
7 4  

Étape 492 :
6 2 1
5 8  
7 4 3

Étape 493 :
6 2  
5 8 1
7 4 3

Étape 494 :
6   2
5 8 1
7 4 3

Étape 495 :
6 8 2
5   1
7 4 3

Étape 496 :
6 8 2
5 4 1
7   3

Étape 497 :
6 8 2
5 4 1
7 3  

Étape 498 :
6 8 2
5 4  
7 3 1

Étape 499 :
6 8  
5 4 2
7 3 1

Étape 500 :
6   8
5 4 2
7 3 1

Étape 501 :
6 4 8
5   2
7 3 1

Étape 502 :
6 4 8
5 3 2
7   1

Étape 503 :
6 4 8
5 3 2
  7 1

Étape 504 :
6 4 8
  3 2
5 7 1

Étape 505 :
  4 8
6 3 2
5 7 1

Étape 506 :
4   8
6 3 2
5 7 1

Étape 507 :
4 3 8
6   2
5 7 1

Étape 508 :
4 3 8
6 7 2
5   1

Étape 509 :
4 3 8
6 7 2
5 1  

Étape 510 :
4 3 8
6 7  
5 1 2

Étape 511 :
4 3  
6 7 8
5 1 2

Étape 512 :
4   3
6 7 8
5 1 2

Étape 513 :
4 7 3
6   8
5 1 2

Étape 514 :
4 7 3
6 1 8
5   2

Étape 515 :
4 7 3
6 1 8
5 2  

Étape 516 :
4 7 3
6 1  
5 2 8

Étape 517 :
4 7  
6 1 3
5 2 8

Étape 518 :
4   7
6 1 3
5 2 8

Étape 519 :
4 1 7
6   3
5 2 8

Étape 520 :
4 1 7
6 2 3
5   8

Étape 521 :
4 1 7
6 2 3
5 8  

Étape 522 :
4 1 7
6 2  
5 8 3

Étape 523 :
4 1  
6 2 7
5 8 3

Étape 524 :
4   1
6 2 7
5 8 3

Étape 525 :
4 2 1
6   7
5 8 3

Étape 526 :
4 2 1
6 8 7
5   3

Étape 527 :
4 2 1
6 8 7
5 3  

Étape 528 :
4 2 1
6 8  
5 3 7

Étape 529 :
4 2  
6 8 1
5 3 7

Étape 530 :
4   2
6 8 1
5 3 7

Étape 531 :
4 8 2
6   1
5 3 7

Étape 532 :
4 8 2
6 3 1
5   7

Étape 533 :
4 8 2
6 3 1
5 7  

Étape 534 :
4 8 2
6 3  
5 7 1

Étape 535 :
4 8 2
6   3
5 7 1

Étape 536 :
4 8 2
6 7 3
5   1

Étape 537 :
4 8 2
6 7 3
5 1  

Étape 538 :
4 8 2
6 7  
5 1 3

Étape 539 :
4 8  
6 7 2
5 1 3

Étape 540 :
4   8
6 7 2
5 1 3

Étape 541 :
4 7 8
6   2
5 1 3

Étape 542 :
4 7 8
6 1 2
5   3

Étape 543 :
4 7 8
6 1 2
5 3  

Étape 544 :
4 7 8
6 1  
5 3 2

Étape 545 :
4 7  
6 1 8
5 3 2

Étape 546 :
4   7
6 1 8
5 3 2

Étape 547 :
4 1 7
6   8
5 3 2

Étape 548 :
4 1 7
6 3 8
5   2

Étape 549 :
4 1 7
6 3 8
  5 2

Étape 550 :
4 1 7
  3 8
6 5 2

Étape 551 :
  1 7
4 3 8
6 5 2

Étape 552 :
1   7
4 3 8
6 5 2

Étape 553 :
1 3 7
4   8
6 5 2

Étape 554 :
1 3 7
4 5 8
6   2

Étape 555 :
1 3 7
4 5 8
6 2  

Étape 556 :
1 3 7
4 5  
6 2 8

Étape 557 :
1 3  
4 5 7
6 2 8

Étape 558 :
1   3
4 5 7
6 2 8

Étape 559 :
1 5 3
4   7
6 2 8

Étape 560 :
1 5 3
4 2 7
6   8

Étape 561 :
1 5 3
4 2 7
6 8  

Étape 562 :
1 5 3
4 2  
6 8 7

Étape 563 :
1 5  
4 2 3
6 8 7

Étape 564 :
1   5
4 2 3
6 8 7

Étape 565 :
1 2 5
4   3
6 8 7

Étape 566 :
1 2 5
4 8 3
6   7

Étape 567 :
1 2 5
4 8 3
6 7  

Étape 568 :
1 2 5
4 8  
6 7 3

Étape 569 :
1 2  
4 8 5
6 7 3

Étape 570 :
1   2
4 8 5
6 7 3

Étape 571 :
1 8 2
4   5
6 7 3

Étape 572 :
1 8 2
4 7 5
6   3

Étape 573 :
1 8 2
4 7 5
6 3  

Étape 574 :
1 8 2
4 7  
6 3 5

Étape 575 :
1 8  
4 7 2
6 3 5

Étape 576 :
1   8
4 7 2
6 3 5

Étape 577 :
1 7 8
4   2
6 3 5

Étape 578 :
1 7 8
4 3 2
6   5

Étape 579 :
1 7 8
4 3 2
6 5  

Étape 580 :
1 7 8
4 3  
6 5 2

Étape 581 :
1 7 8
4   3
6 5 2

Étape 582 :
1 7 8
4 5 3
6   2

Étape 583 :
1 7 8
4 5 3
6 2  

Étape 584 :
1 7 8
4 5  
6 2 3

Étape 585 :
1 7  
4 5 8
6 2 3

Étape 586 :
1   7
4 5 8
6 2 3

Étape 587 :
1 5 7
4   8
6 2 3

Étape 588 :
1 5 7
4 2 8
6   3

Étape 589 :
1 5 7
4 2 8
6 3  

Étape 590 :
1 5 7
4 2  
6 3 8

Étape 591 :
1 5  
4 2 7
6 3 8

Étape 592 :
1   5
4 2 7
6 3 8

Étape 593 :
1 2 5
4   7
6 3 8

Étape 594 :
1 2 5
4 3 7
6   8

Étape 595 :
1 2 5
4 3 7
  6 8

Étape 596 :
1 2 5
  3 7
4 6 8

Étape 597 :
  2 5
1 3 7
4 6 8

Étape 598 :
2   5
1 3 7
4 6 8

Étape 599 :
2 3 5
1   7
4 6 8

Étape 600 :
2 3 5
1 6 7
4   8

Étape 601 :
2 3 5
1 6 7
4 8  

Étape 602 :
2 3 5
1 6  
4 8 7

Étape 603 :
2 3  
1 6 5
4 8 7

Étape 604 :
2   3
1 6 5
4 8 7

Étape 605 :
2 6 3
1   5
4 8 7

Étape 606 :
2 6 3
1 8 5
4   7

Étape 607 :
2 6 3
1 8 5
4 7  

Étape 608 :
2 6 3
1 8  
4 7 5

Étape 609 :
2 6  
1 8 3
4 7 5

Étape 610 :
2   6
1 8 3
4 7 5

Étape 611 :
2 8 6
1   3
4 7 5

Étape 612 :
2 8 6
1 7 3
4   5

Étape 613 :
2 8 6
1 7 3
4 5  

Étape 614 :
2 8 6
1 7  
4 5 3

Étape 615 :
2 8  
1 7 6
4 5 3

Étape 616 :
2   8
1 7 6
4 5 3

Étape 617 :
2 7 8
1   6
4 5 3

Étape 618 :
2 7 8
1 5 6
4   3

Étape 619 :
2 7 8
1 5 6
4 3  

Étape 620 :
2 7 8
1 5  
4 3 6

Étape 621 :
2 7  
1 5 8
4 3 6

Étape 622 :
2   7
1 5 8
4 3 6

Étape 623 :
2 5 7
1   8
4 3 6

Étape 624 :
2 5 7
1 3 8
4   6

Étape 625 :
2 5 7
1 3 8
4 6  

Étape 626 :
2 5 7
1 3  
4 6 8

Étape 627 :
2 5 7
1   3
4 6 8

Étape 628 :
2 5 7
1 6 3
4   8

Étape 629 :
2 5 7
1 6 3
4 8  

Étape 630 :
2 5 7
1 6  
4 8 3

Étape 631 :
2 5  
1 6 7
4 8 3

Étape 632 :
2   5
1 6 7
4 8 3

Étape 633 :
2 6 5
1   7
4 8 3

Étape 634 :
2 6 5
1 8 7
4   3

Étape 635 :
2 6 5
1 8 7
4 3  

Étape 636 :
2 6 5
1 8  
4 3 7

Étape 637 :
2 6  
1 8 5
4 3 7

Étape 638 :
2   6
1 8 5
4 3 7

Étape 639 :
2 8 6
1   5
4 3 7

Étape 640 :
2 8 6
1 3 5
4   7

Étape 641 :
2 8 6
1 3 5
  4 7

Étape 642 :
2 8 6
  3 5
1 4 7

Étape 643 :
  8 6
2 3 5
1 4 7

Étape 644 :
8   6
2 3 5
1 4 7

Étape 645 :
8 3 6
2   5
1 4 7

Étape 646 :
8 3 6
2 4 5
1   7

Étape 647 :
8 3 6
2 4 5
  1 7

Étape 648 :
8 3 6
  4 5
2 1 7

Étape 649 :
  3 6
8 4 5
2 1 7

Étape 650 :
3   6
8 4 5
2 1 7

Étape 651 :
3 4 6
8   5
2 1 7

Étape 652 :
3 4 6
8 1 5
2   7

Étape 653 :
3 4 6
8 1 5
2 7  

Étape 654 :
3 4 6
8 1  
2 7 5

Étape 655 :
3 4  
8 1 6
2 7 5

Étape 656 :
3   4
8 1 6
2 7 5

Étape 657 :
3 1 4
8   6
2 7 5

Étape 658 :
3 1 4
8 7 6
2   5

Étape 659 :
3 1 4
8 7 6
2 5  

Étape 660 :
3 1 4
8 7  
2 5 6

Étape 661 :
3 1  
8 7 4
2 5 6

Étape 662 :
3   1
8 7 4
2 5 6

Étape 663 :
3 7 1
8   4
2 5 6

Étape 664 :
3 7 1
8 5 4
2   6

Étape 665 :
3 7 1
8 5 4
2 6  

Étape 666 :
3 7 1
8 5  
2 6 4

Étape 667 :
3 7  
8 5 1
2 6 4

Étape 668 :
3   7
8 5 1
2 6 4

Étape 669 :
3 5 7
8   1
2 6 4

Étape 670 :
3 5 7
8 6 1
2   4

Étape 671 :
3 5 7
8 6 1
2 4  

Étape 672 :
3 5 7
8 6  
2 4 1

Étape 673 :
3 5  
8 6 7
2 4 1

Étape 674 :
3   5
8 6 7
2 4 1

Étape 675 :
3 6 5
8   7
2 4 1

Étape 676 :
3 6 5
8 4 7
2   1

Étape 677 :
3 6 5
8 4 7
2 1  

Étape 678 :
3 6 5
8 4  
2 1 7

Étape 679 :
3 6 5
8   4
2 1 7

Étape 680 :
3 6 5
8 1 4
2   7

Étape 681 :
3 6 5
8 1 4
2 7  

Étape 682 :
3 6 5
8 1  
2 7 4

Étape 683 :
3 6  
8 1 5
2 7 4

Étape 684 :
3   6
8 1 5
2 7 4

Étape 685 :
3 1 6
8   5
2 7 4

Étape 686 :
3 1 6
8 7 5
2   4

Étape 687 :
3 1 6
8 7 5
2 4  

Étape 688 :
3 1 6
8 7  
2 4 5

Étape 689 :
3 1  
8 7 6
2 4 5

Étape 690 :
3   1
8 7 6
2 4 5

Étape 691 :
3 7 1
8   6
2 4 5

Étape 692 :
3 7 1
8 4 6
2   5

Étape 693 :
3 7 1
8 4 6
  2 5

Étape 694 :
3 7 1
  4 6
8 2 5

Étape 695 :
  7 1
3 4 6
8 2 5

Étape 696 :
7   1
3 4 6
8 2 5

Étape 697 :
7 4 1
3   6
8 2 5

Étape 698 :
7 4 1
3 2 6
8   5

Étape 699 :
7 4 1
3 2 6
8 5  

Étape 700 :
7 4 1
3 2  
8 5 6

Étape 701 :
7 4  
3 2 1
8 5 6

Étape 702 :
7   4
3 2 1
8 5 6

Étape 703 :
7 2 4
3   1
8 5 6

Étape 704 :
7 2 4
3 5 1
8   6

Étape 705 :
7 2 4
3 5 1
8 6  

Étape 706 :
7 2 4
3 5  
8 6 1

Étape 707 :
7 2  
3 5 4
8 6 1

Étape 708 :
7   2
3 5 4
8 6 1

Étape 709 :
7 5 2
3   4
8 6 1

Étape 710 :
7 5 2
3 6 4
8   1

Étape 711 :
7 5 2
3 6 4
8 1  

Étape 712 :
7 5 2
3 6  
8 1 4

Étape 713 :
7 5  
3 6 2
8 1 4

Étape 714 :
7   5
3 6 2
8 1 4

Étape 715 :
7 6 5
3   2
8 1 4

Étape 716 :
7 6 5
3 1 2
8   4

Étape 717 :
7 6 5
3 1 2
8 4  

Étape 718 :
7 6 5
3 1  
8 4 2

Étape 719 :
7 6  
3 1 5
8 4 2

Étape 720 :
7   6
3 1 5
8 4 2

Étape 721 :
7 1 6
3   5
8 4 2

Étape 722 :
7 1 6
3 4 5
8   2

Étape 723 :
7 1 6
3 4 5
8 2  

Étape 724 :
7 1 6
3 4  
8 2 5

Étape 725 :
7 1 6
3   4
8 2 5

Étape 726 :
7 1 6
3 2 4
8   5

Étape 727 :
7 1 6
3 2 4
8 5  

Étape 728 :
7 1 6
3 2  
8 5 4

Étape 729 :
7 1  
3 2 6
8 5 4

Étape 730 :
7   1
3 2 6
8 5 4

Étape 731 :
7 2 1
3   6
8 5 4

Étape 732 :
7 2 1
3 5 6
8   4

Étape 733 :
7 2 1
3 5 6
8 4  

Étape 734 :
7 2 1
3 5  
8 4 6

Étape 735 :
7 2  
3 5 1
8 4 6

Étape 736 :
7   2
3 5 1
8 4 6

Étape 737 :
7 5 2
3   1
8 4 6

Étape 738 :
7 5 2
3 4 1
8   6

Étape 739 :
7 5 2
3 4 1
  8 6

Étape 740 :
7 5 2
  4 1
3 8 6

Étape 741 :
  5 2
7 4 1
3 8 6

Étape 742 :
5   2
7 4 1
3 8 6

Étape 743 :
5 4 2
7   1
3 8 6

Étape 744 :
5 4 2
7 8 1
3   6

Étape 745 :
5 4 2
7 8 1
3 6  

Étape 746 :
5 4 2
7 8  
3 6 1

Étape 747 :
5 4  
7 8 2
3 6 1

Étape 748 :
5   4
7 8 2
3 6 1

Étape 749 :
5 8 4
7   2
3 6 1

Étape 750 :
5 8 4
7 6 2
3   1

Étape 751 :
5 8 4
7 6 2
3 1  

Étape 752 :
5 8 4
7 6  
3 1 2

Étape 753 :
5 8  
7 6 4
3 1 2

Étape 754 :
5   8
7 6 4
3 1 2

Étape 755 :
5 6 8
7   4
3 1 2

Étape 756 :
5 6 8
7 1 4
3   2

Étape 757 :
5 6 8
7 1 4
3 2  

Étape 758 :
5 6 8
7 1  
3 2 4

Étape 759 :
5 6  
7 1 8
3 2 4

Étape 760 :
5   6
7 1 8
3 2 4

Étape 761 :
5 1 6
7   8
3 2 4

Étape 762 :
5 1 6
7 2 8
3   4

Étape 763 :
5 1 6
7 2 8
3 4  

Étape 764 :
5 1 6
7 2  
3 4 8

Étape 765 :
5 1  
7 2 6
3 4 8

Étape 766 :
5   1
7 2 6
3 4 8

Étape 767 :
5 2 1
7   6
3 4 8

Étape 768 :
5 2 1
7 4 6
3   8

Étape 769 :
5 2 1
7 4 6
3 8  

Étape 770 :
5 2 1
7 4  
3 8 6

Étape 771 :
5 2 1
7   4
3 8 6

Étape 772 :
5 2 1
7 8 4
3   6

Étape 773 :
5 2 1
7 8 4
3 6  

Étape 774 :
5 2 1
7 8  
3 6 4

Étape 775 :
5 2  
7 8 1
3 6 4

Étape 776 :
5   2
7 8 1
3 6 4

Étape 777 :
5 8 2
7   1
3 6 4

Étape 778 :
5 8 2
7 6 1
3   4

Étape 779 :
5 8 2
7 6 1
3 4  

Étape 780 :
5 8 2
7 6  
3 4 1

Étape 781 :
5 8  
7 6 2
3 4 1

Étape 782 :
5   8
7 6 2
3 4 1

Étape 783 :
5 6 8
7   2
3 4 1

Étape 784 :
5 6 8
7 4 2
3   1

Étape 785 :
5 6 8
7 4 2
  3 1

Étape 786 :
5 6 8
  4 2
7 3 1

Étape 787 :
5 6 8
4   2
7 3 1

Étape 788 :
5 6 8
4 3 2
7   1

Étape 789 :
5 6 8
4 3 2
7 1  

Étape 790 :
5 6 8
4 3  
7 1 2

Étape 791 :
5 6  
4 3 8
7 1 2

Étape 792 :
5   6
4 3 8
7 1 2

Étape 793 :
5 3 6
4   8
7 1 2

Étape 794 :
5 3 6
4 1 8
7   2

Étape 795 :
5 3 6
4 1 8
7 2  

Étape 796 :
5 3 6
4 1  
7 2 8

Étape 797 :
5 3  
4 1 6
7 2 8

Étape 798 :
5   3
4 1 6
7 2 8

Étape 799 :
5 1 3
4   6
7 2 8

Étape 800 :
5 1 3
4 2 6
7   8

Étape 801 :
5 1 3
4 2 6
7 8  

Étape 802 :
5 1 3
4 2  
7 8 6

Étape 803 :
5 1  
4 2 3
7 8 6

Étape 804 :
5   1
4 2 3
7 8 6

Étape 805 :
5 2 1
4   3
7 8 6

Étape 806 :
5 2 1
4 8 3
7   6

Étape 807 :
5 2 1
4 8 3
7 6  

Étape 808 :
5 2 1
4 8  
7 6 3

Étape 809 :
5 2  
4 8 1
7 6 3

Étape 810 :
5   2
4 8 1
7 6 3

Étape 811 :
5 8 2
4   1
7 6 3

Étape 812 :
5 8 2
4 6 1
7   3

Étape 813 :
5 8 2
4 6 1
7 3  

Étape 814 :
5 8 2
4 6  
7 3 1

Étape 815 :
5 8 2
4   6
7 3 1

Étape 816 :
5 8 2
4 3 6
7   1

Étape 817 :
5 8 2
4 3 6
7 1  

Étape 818 :
5 8 2
4 3  
7 1 6

Étape 819 :
5 8  
4 3 2
7 1 6

Étape 820 :
5   8
4 3 2
7 1 6

Étape 821 :
5 3 8
4   2
7 1 6

Étape 822 :
5 3 8
4 1 2
7   6

Étape 823 :
5 3 8
4 1 2
7 6  

Étape 824 :
5 3 8
4 1  
7 6 2

Étape 825 :
5 3  
4 1 8
7 6 2

Étape 826 :
5   3
4 1 8
7 6 2

Étape 827 :
5 1 3
4   8
7 6 2

Étape 828 :
5 1 3
4 6 8
7   2

Étape 829 :
5 1 3
4 6 8
  7 2

Étape 830 :
5 1 3
  6 8
4 7 2

Étape 831 :
  1 3
5 6 8
4 7 2

Étape 832 :
1   3
5 6 8
4 7 2

Étape 833 :
1 6 3
5   8
4 7 2

Étape 834 :
1 6 3
5 7 8
4   2

Étape 835 :
1 6 3
5 7 8
4 2  

Étape 836 :
1 6 3
5 7  
4 2 8

Étape 837 :
1 6  
5 7 3
4 2 8

Étape 838 :
1   6
5 7 3
4 2 8

Étape 839 :
1 7 6
5   3
4 2 8

Étape 840 :
1 7 6
5 2 3
4   8

Étape 841 :
1 7 6
5 2 3
4 8  

Étape 842 :
1 7 6
5 2  
4 8 3

Étape 843 :
1 7  
5 2 6
4 8 3

Étape 844 :
1   7
5 2 6
4 8 3

Étape 845 :
1 2 7
5   6
4 8 3

Étape 846 :
1 2 7
5 8 6
4   3

Étape 847 :
1 2 7
5 8 6
4 3  

Étape 848 :
1 2 7
5 8  
4 3 6

Étape 849 :
1 2  
5 8 7
4 3 6

Étape 850 :
1   2
5 8 7
4 3 6

Étape 851 :
1 8 2
5   7
4 3 6

Étape 852 :
1 8 2
5 3 7
4   6

Étape 853 :
1 8 2
5 3 7
4 6  

Étape 854 :
1 8 2
5 3  
4 6 7

Étape 855 :
1 8  
5 3 2
4 6 7

Étape 856 :
1   8
5 3 2
4 6 7

Étape 857 :
1 3 8
5   2
4 6 7

Étape 858 :
1 3 8
5 6 2
4   7

Étape 859 :
1 3 8
5 6 2
4 7  

Étape 860 :
1 3 8
5 6  
4 7 2

Étape 861 :
1 3 8
5   6
4 7 2

Étape 862 :
1 3 8
5 7 6
4   2

Étape 863 :
1 3 8
5 7 6
4 2  

Étape 864 :
1 3 8
5 7  
4 2 6

Étape 865 :
1 3  
5 7 8
4 2 6

Étape 866 :
1   3
5 7 8
4 2 6

Étape 867 :
1 7 3
5   8
4 2 6

Étape 868 :
1 7 3
5 2 8
4   6

Étape 869 :
1 7 3
5 2 8
4 6  

Étape 870 :
1 7 3
5 2  
4 6 8

Étape 871 :
1 7  
5 2 3
4 6 8

Étape 872 :
1   7
5 2 3
4 6 8

Étape 873 :
1 2 7
5   3
4 6 8

Étape 874 :
1 2 7
5 6 3
4   8

Étape 875 :
1 2 7
5 6 3
  4 8

Étape 876 :
1 2 7
  6 3
5 4 8

Étape 877 :
  2 7
1 6 3
5 4 8

Étape 878 :
2   7
1 6 3
5 4 8

Étape 879 :
2 6 7
1   3
5 4 8

Étape 880 :
2 6 7
1 4 3
5   8

Étape 881 :
2 6 7
1 4 3
5 8  

Étape 882 :
2 6 7
1 4  
5 8 3

Étape 883 :
2 6  
1 4 7
5 8 3

Étape 884 :
2   6
1 4 7
5 8 3

Étape 885 :
2 4 6
1   7
5 8 3

Étape 886 :
2 4 6
1 8 7
5   3

Étape 887 :
2 4 6
1 8 7
5 3  

Étape 888 :
2 4 6
1 8  
5 3 7

Étape 889 :
2 4  
1 8 6
5 3 7

Étape 890 :
2   4
1 8 6
5 3 7

Étape 891 :
2 8 4
1   6
5 3 7

Étape 892 :
2 8 4
1 3 6
5   7

Étape 893 :
2 8 4
1 3 6
5 7  

Étape 894 :
2 8 4
1 3  
5 7 6

Étape 895 :
2 8  
1 3 4
5 7 6

Étape 896 :
2   8
1 3 4
5 7 6

Étape 897 :
2 3 8
1   4
5 7 6

Étape 898 :
2 3 8
1 7 4
5   6

Étape 899 :
2 3 8
1 7 4
5 6  

Étape 900 :
2 3 8
1 7  
5 6 4

Étape 901 :
2 3  
1 7 8
5 6 4

Étape 902 :
2   3
1 7 8
5 6 4

Étape 903 :
2 7 3
1   8
5 6 4

Étape 904 :
2 7 3
1 6 8
5   4

Étape 905 :
2 7 3
1 6 8
5 4  

Étape 906 :
2 7 3
1 6  
5 4 8

Étape 907 :
2 7 3
1   6
5 4 8

Étape 908 :
2 7 3
1 4 6
5   8

Étape 909 :
2 7 3
1 4 6
5 8  

Étape 910 :
2 7 3
1 4  
5 8 6

Étape 911 :
2 7  
1 4 3
5 8 6

Étape 912 :
2   7
1 4 3
5 8 6

Étape 913 :
2 4 7
1   3
5 8 6

Étape 914 :
2 4 7
1 8 3
5   6

Étape 915 :
2 4 7
1 8 3
5 6  

Étape 916 :
2 4 7
1 8  
5 6 3

Étape 917 :
2 4  
1 8 7
5 6 3

Étape 918 :
2   4
1 8 7
5 6 3

Étape 919 :
2 8 4
1   7
5 6 3

Étape 920 :
2 8 4
1 6 7
5   3

Étape 921 :
2 8 4
1 6 7
  5 3

Étape 922 :
2 8 4
  6 7
1 5 3

Étape 923 :
  8 4
2 6 7
1 5 3

Étape 924 :
8   4
2 6 7
1 5 3

Étape 925 :
8 6 4
2   7
1 5 3

Étape 926 :
8 6 4
2 5 7
1   3

Étape 927 :
8 6 4
2 5 7
  1 3

Étape 928 :
8 6 4
  5 7
2 1 3

Étape 929 :
  6 4
8 5 7
2 1 3

Étape 930 :
6   4
8 5 7
2 1 3

Étape 931 :
6 5 4
8   7
2 1 3

Étape 932 :
6 5 4
8 1 7
2   3

Étape 933 :
6 5 4
8 1 7
2 3  

Étape 934 :
6 5 4
8 1  
2 3 7

Étape 935 :
6 5  
8 1 4
2 3 7

Étape 936 :
6   5
8 1 4
2 3 7

Étape 937 :
6 1 5
8   4
2 3 7

Étape 938 :
6 1 5
8 3 4
2   7

Étape 939 :
6 1 5
8 3 4
2 7  

Étape 940 :
6 1 5
8 3  
2 7 4

Étape 941 :
6 1  
8 3 5
2 7 4

Étape 942 :
6   1
8 3 5
2 7 4

Étape 943 :
6 3 1
8   5
2 7 4

Étape 944 :
6 3 1
8 7 5
2   4

Étape 945 :
6 3 1
8 7 5
2 4  

Étape 946 :
6 3 1
8 7  
2 4 5

Étape 947 :
6 3  
8 7 1
2 4 5

Étape 948 :
6   3
8 7 1
2 4 5

Étape 949 :
6 7 3
8   1
2 4 5

Étape 950 :
6 7 3
8 4 1
2   5

Étape 951 :
6 7 3
8 4 1
2 5  

Étape 952 :
6 7 3
8 4  
2 5 1

Étape 953 :
6 7  
8 4 3
2 5 1

Étape 954 :
6   7
8 4 3
2 5 1

Étape 955 :
6 4 7
8   3
2 5 1

Étape 956 :
6 4 7
8 5 3
2   1

Étape 957 :
6 4 7
8 5 3
2 1  

Étape 958 :
6 4 7
8 5  
2 1 3

Étape 959 :
6 4 7
8   5
2 1 3

Étape 960 :
6 4 7
8 1 5
2   3

Étape 961 :
6 4 7
8 1 5
2 3  

Étape 962 :
6 4 7
8 1  
2 3 5

Étape 963 :
6 4  
8 1 7
2 3 5

Étape 964 :
6   4
8 1 7
2 3 5

Étape 965 :
6 1 4
8   7
2 3 5

Étape 966 :
6 1 4
8 3 7
2   5

Étape 967 :
6 1 4
8 3 7
2 5  

Étape 968 :
6 1 4
8 3  
2 5 7

Étape 969 :
6 1  
8 3 4
2 5 7

Étape 970 :
6   1
8 3 4
2 5 7

Étape 971 :
6 3 1
8   4
2 5 7

Étape 972 :
6 3 1
8 5 4
2   7

Étape 973 :
6 3 1
8 5 4
  2 7

Étape 974 :
6 3 1
  5 4
8 2 7

Étape 975 :
  3 1
6 5 4
8 2 7

Étape 976 :
3   1
6 5 4
8 2 7

Étape 977 :
3 5 1
6   4
8 2 7

Étape 978 :
3 5 1
6 2 4
8   7

Étape 979 :
3 5 1
6 2 4
8 7  

Étape 980 :
3 5 1
6 2  
8 7 4

Étape 981 :
3 5  
6 2 1
8 7 4

Étape 982 :
3   5
6 2 1
8 7 4

Étape 983 :
3 2 5
6   1
8 7 4

Étape 984 :
3 2 5
6 7 1
8   4

Étape 985 :
3 2 5
6 7 1
8 4  

Étape 986 :
3 2 5
6 7  
8 4 1

Étape 987 :
3 2  
6 7 5
8 4 1

Étape 988 :
3   2
6 7 5
8 4 1

Étape 989 :
3 7 2
6   5
8 4 1

Étape 990 :
3 7 2
6 4 5
8   1

Étape 991 :
3 7 2
6 4 5
8 1  

Étape 992 :
3 7 2
6 4  
8 1 5

Étape 993 :
3 7  
6 4 2
8 1 5

Étape 994 :
3   7
6 4 2
8 1 5

Étape 995 :
3 4 7
6   2
8 1 5

Étape 996 :
3 4 7
6 1 2
8   5

Étape 997 :
3 4 7
6 1 2
8 5  

Étape 998 :
3 4 7
6 1  
8 5 2

Étape 999 :
3 4  
6 1 7
8 5 2

Étape 1000 :
3   4
6 1 7
8 5 2

Étape 1001 :
3 1 4
6   7
8 5 2

Étape 1002 :
3 1 4
6 5 7
8   2

Étape 1003 :
3 1 4
6 5 7
8 2  

Étape 1004 :
3 1 4
6 5  
8 2 7

Étape 1005 :
3 1 4
6   5
8 2 7

Étape 1006 :
3 1 4
6 2 5
8   7

Étape 1007 :
3 1 4
6 2 5
8 7  

Étape 1008 :
3 1 4
6 2  
8 7 5

Étape 1009 :
3 1  
6 2 4
8 7 5

Étape 1010 :
3   1
6 2 4
8 7 5

Étape 1011 :
3 2 1
6   4
8 7 5

Étape 1012 :
3 2 1
6 7 4
8   5

Étape 1013 :
3 2 1
6 7 4
8 5  

Étape 1014 :
3 2 1
6 7  
8 5 4

Étape 1015 :
3 2  
6 7 1
8 5 4

Étape 1016 :
3   2
6 7 1
8 5 4

Étape 1017 :
3 7 2
6   1
8 5 4

Étape 1018 :
3 7 2
6 5 1
8   4

Étape 1019 :
3 7 2
6 5 1
  8 4

Étape 1020 :
3 7 2
  5 1
6 8 4

Étape 1021 :
  7 2
3 5 1
6 8 4

Étape 1022 :
7   2
3 5 1
6 8 4

Étape 1023 :
7 5 2
3   1
6 8 4

Étape 1024 :
7 5 2
3 8 1
6   4

Étape 1025 :
7 5 2
3 8 1
6 4  

Étape 1026 :
7 5 2
3 8  
6 4 1

Étape 1027 :
7 5  
3 8 2
6 4 1

Étape 1028 :
7   5
3 8 2
6 4 1

Étape 1029 :
7 8 5
3   2
6 4 1

Étape 1030 :
7 8 5
3 4 2
6   1

Étape 1031 :
7 8 5
3 4 2
6 1  

Étape 1032 :
7 8 5
3 4  
6 1 2

Étape 1033 :
7 8  
3 4 5
6 1 2

Étape 1034 :
7   8
3 4 5
6 1 2

Étape 1035 :
7 4 8
3   5
6 1 2

Étape 1036 :
7 4 8
3 1 5
6   2

Étape 1037 :
7 4 8
3 1 5
6 2  

Étape 1038 :
7 4 8
3 1  
6 2 5

Étape 1039 :
7 4  
3 1 8
6 2 5

Étape 1040 :
7   4
3 1 8
6 2 5

Étape 1041 :
7 1 4
3   8
6 2 5

Étape 1042 :
7 1 4
3 2 8
6   5

Étape 1043 :
7 1 4
3 2 8
6 5  

Étape 1044 :
7 1 4
3 2  
6 5 8

Étape 1045 :
7 1  
3 2 4
6 5 8

Étape 1046 :
7   1
3 2 4
6 5 8

Étape 1047 :
7 2 1
3   4
6 5 8

Étape 1048 :
7 2 1
3 5 4
6   8

Étape 1049 :
7 2 1
3 5 4
6 8  

Étape 1050 :
7 2 1
3 5  
6 8 4

Étape 1051 :
7 2 1
3   5
6 8 4

Étape 1052 :
7 2 1
3 8 5
6   4

Étape 1053 :
7 2 1
3 8 5
6 4  

Étape 1054 :
7 2 1
3 8  
6 4 5

Étape 1055 :
7 2  
3 8 1
6 4 5

Étape 1056 :
7   2
3 8 1
6 4 5

Étape 1057 :
7 8 2
3   1
6 4 5

Étape 1058 :
7 8 2
3 4 1
6   5

Étape 1059 :
7 8 2
3 4 1
6 5  

Étape 1060 :
7 8 2
3 4  
6 5 1

Étape 1061 :
7 8  
3 4 2
6 5 1

Étape 1062 :
7   8
3 4 2
6 5 1

Étape 1063 :
7 4 8
3   2
6 5 1

Étape 1064 :
7 4 8
3 5 2
6   1

Étape 1065 :
7 4 8
3 5 2
  6 1

Étape 1066 :
7 4 8
  5 2
3 6 1

Étape 1067 :
  4 8
7 5 2
3 6 1

Étape 1068 :
4   8
7 5 2
3 6 1

Étape 1069 :
4 5 8
7   2
3 6 1

Étape 1070 :
4 5 8
7 6 2
3   1

Étape 1071 :
4 5 8
7 6 2
3 1  

Étape 1072 :
4 5 8
7 6  
3 1 2

Étape 1073 :
4 5  
7 6 8
3 1 2

Étape 1074 :
4   5
7 6 8
3 1 2

Étape 1075 :
4 6 5
7   8
3 1 2

Étape 1076 :
4 6 5
7 1 8
3   2

Étape 1077 :
4 6 5
7 1 8
3 2  

Étape 1078 :
4 6 5
7 1  
3 2 8

Étape 1079 :
4 6  
7 1 5
3 2 8

Étape 1080 :
4   6
7 1 5
3 2 8

Étape 1081 :
4 1 6
7   5
3 2 8

Étape 1082 :
4 1 6
7 2 5
3   8

Étape 1083 :
4 1 6
7 2 5
3 8  

Étape 1084 :
4 1 6
7 2  
3 8 5

Étape 1085 :
4 1  
7 2 6
3 8 5

Étape 1086 :
4   1
7 2 6
3 8 5

Étape 1087 :
4 2 1
7   6
3 8 5

Étape 1088 :
4 2 1
7 8 6
3   5

Étape 1089 :
4 2 1
7 8 6
3 5  

Étape 1090 :
4 2 1
7 8  
3 5 6

Étape 1091 :
4 2  
7 8 1
3 5 6

Étape 1092 :
4   2
7 8 1
3 5 6

Étape 1093 :
4 8 2
7   1
3 5 6

Étape 1094 :
4 8 2
7 5 1
3   6

Étape 1095 :
4 8 2
7 5 1
3 6  

Étape 1096 :
4 8 2
7 5  
3 6 1

Étape 1097 :
4 8 2
7   5
3 6 1

Étape 1098 :
4 8 2
7 6 5
3   1

Étape 1099 :
4 8 2
7 6 5
3 1  

Étape 1100 :
4 8 2
7 6  
3 1 5

Étape 1101 :
4 8  
7 6 2
3 1 5

Étape 1102 :
4   8
7 6 2
3 1 5

Étape 1103 :
4 6 8
7   2
3 1 5

Étape 1104 :
4 6 8
7 1 2
3   5

Étape 1105 :
4 6 8
7 1 2
3 5  

Étape 1106 :
4 6 8
7 1  
3 5 2

Étape 1107 :
4 6  
7 1 8
3 5 2

Étape 1108 :
4   6
7 1 8
3 5 2

Étape 1109 :
4 1 6
7   8
3 5 2

Étape 1110 :
4 1 6
7 5 8
3   2

Étape 1111 :
4 1 6
7 5 8
  3 2

Étape 1112 :
4 1 6
  5 8
7 3 2

Étape 1113 :
  1 6
4 5 8
7 3 2

Étape 1114 :
1   6
4 5 8
7 3 2

Étape 1115 :
1 5 6
4   8
7 3 2

Étape 1116 :
1 5 6
4 3 8
7   2

Étape 1117 :
1 5 6
4 3 8
7 2  

Étape 1118 :
1 5 6
4 3  
7 2 8

Étape 1119 :
1 5  
4 3 6
7 2 8

Étape 1120 :
1   5
4 3 6
7 2 8

Étape 1121 :
1 3 5
4   6
7 2 8

Étape 1122 :
1 3 5
4 2 6
7   8

Étape 1123 :
1 3 5
4 2 6
7 8  

Étape 1124 :
1 3 5
4 2  
7 8 6

Étape 1125 :
1 3  
4 2 5
7 8 6

Étape 1126 :
1   3
4 2 5
7 8 6

Étape 1127 :
1 2 3
4   5
7 8 6

Étape 1128 :
1 2 3
4 8 5
7   6

Étape 1129 :
1 2 3
4 8 5
7 6  

Étape 1130 :
1 2 3
4 8  
7 6 5

Étape 1131 :
1 2  
4 8 3
7 6 5

Étape 1132 :
1   2
4 8 3
7 6 5

Étape 1133 :
1 8 2
4   3
7 6 5

Étape 1134 :
1 8 2
4 6 3
7   5

Étape 1135 :
1 8 2
4 6 3
7 5  

Étape 1136 :
1 8 2
4 6  
7 5 3

Étape 1137 :
1 8  
4 6 2
7 5 3

Étape 1138 :
1   8
4 6 2
7 5 3

Étape 1139 :
1 6 8
4   2
7 5 3

Étape 1140 :
1 6 8
4 5 2
7   3

Étape 1141 :
1 6 8
4 5 2
7 3  

Étape 1142 :
1 6 8
4 5  
7 3 2

Étape 1143 :
1 6 8
4   5
7 3 2

Étape 1144 :
1 6 8
4 3 5
7   2

Étape 1145 :
1 6 8
4 3 5
7 2  

Étape 1146 :
1 6 8
4 3  
7 2 5

Étape 1147 :
1 6  
4 3 8
7 2 5

Étape 1148 :
1   6
4 3 8
7 2 5

Étape 1149 :
1 3 6
4   8
7 2 5

Étape 1150 :
1 3 6
4 2 8
7   5

Étape 1151 :
1 3 6
4 2 8
7 5  

Étape 1152 :
1 3 6
4 2  
7 5 8

Étape 1153 :
1 3  
4 2 6
7 5 8

Étape 1154 :
1   3
4 2 6
7 5 8

Étape 1155 :
1 2 3
4   6
7 5 8

Étape 1156 :
1 2 3
4 5 6
7   8

Étape 1157 :
1 2 3
4 5 6
7 8

Remarques

La recherche en largeur (BFS) identifie la solution optimale, 25 mouvements, en 145 605 itérations.
La recherche en profondeur (DFS) découvre une solution impliquant 1 157 mouvements en 1 187 itérations.

Comment découvrir des solutions plus efficacement ?

La recherche en profondeur (DFS) produira-t-elle toujours des solutions sous-optimales ?

Non, si la solution optimale se trouve le long du chemin parcouru par la recherche en profondeur (DFS) dans l’arbre de recherche, alors DFS identifiera effectivement la solution optimale.

Est-il possible que DFS découvre des solutions supérieures à la solution optimale ?

Certainement pas ; de telles solutions seraient soit invalides (impliquant des mouvements impossibles), soit indiqueraient une erreur dans votre estimation.

Cela signifie-t-il que la recherche en profondeur (DFS) n’a pas d’applications pratiques ?

Quand est-il approprié d’utiliser DFS ?

La recherche en largeur (BFS) étend sa frontière systématiquement dans toutes les directions, ce qui entraîne une croissance rapide des besoins en mémoire.

En revanche, l’utilisation de la mémoire de DFS est limitée par le nombre de mouvements nécessaires pour atteindre ses points de retour en arrière ou par la longueur du chemin de la première solution trouvée. Dans tous les scénarios, DFS continue d’étendre la frontière dans une direction.

Dans certaines applications où toutes les solutions possibles doivent être explorées, tout l’espace de recherche doit être parcouru. Utiliser BFS dans ces cas serait prohibitif en termes de mémoire. Cependant, DFS peut explorer l’ensemble de l’espace avec une utilisation minimale de la mémoire.

Le langage de programmation Prolog inclut un algorithme de retour en arrière intégré qui énumère toutes les solutions possibles. Le retour en arrière est une variante de DFS efficace en mémoire.

La recherche limitée en profondeur et la recherche en approfondissement itératif seraient des algorithmes de recherche non informée alternatifs.

Trouver des solutions plus efficacement nécessite une connaissance du domaine.

Prologue

Résumé

Justification pour l’étude de la recherche
Terminologie et concepts clés
Algorithmes de recherche non informée
Recherche en largeur (BFS)
Recherche en profondeur (DFS)
Implémentations

Justification pour l’étude de la recherche :
- Mise en avant de la transition de la focalisation exclusive sur l’apprentissage automatique à l’intégration des algorithmes de recherche.
- Souligné le rôle de la recherche dans les systèmes d’IA avancés comme AlphaGo, AlphaZero et MuZero.
- Noté que les algorithmes de recherche sont cruciaux pour la planification, le raisonnement, et seront de plus en plus importants.
Chronologie historique des algorithmes de recherche :
- Présenté une chronologie biaisée de l’algorithme A* de 1968 aux développements récents comme MuZero et Agent57.
- Montre l’évolution de la recherche basée sur des heuristiques à l’intégration de l’apprentissage profond avec les méthodes de recherche.
Applications de la recherche :
- Recherche de chemin et navigation : Trouver des chemins optimaux en robotique et dans les jeux.
- Résolution de puzzles : Résoudre des problèmes comme le 8-Puzzle et le Sudoku.
- Analyse de réseau : Analyser la connectivité et les chemins les plus courts dans les réseaux.
- Jeu : Évaluer des mouvements dans des jeux comme les échecs ou le Go.
- Planification et allocation des ressources : Planifier des tâches et allouer efficacement des ressources.
- Problèmes de configuration : Assembler des composants pour répondre à des exigences spécifiques.
- Prise de décision sous incertitude : Prendre des décisions dans des environnements dynamiques et incertains.
- Narration : Guider les modèles de langage avec des plans d’automates planificateurs.
Terminologie et concepts clés :
- Agent : Une entité qui effectue des actions pour atteindre des objectifs.
- Caractéristiques de l’environnement : Environnements entièrement observables, mono-agents, déterministes, statiques et discrets.
- Définition du problème de recherche :
  - Espace d’états : Tous les états possibles.
  - État initial : Où l’agent commence.
  - État(s) objectif(s) : Résultat(s) souhaité(s).
  - Actions : Déplacements possibles depuis un état.
  - Modèle de transition : Règles déterminant les changements d’état.
  - Fonction de coût d’action : Coût associé aux actions.
Algorithmes de recherche non informée :
- Recherche en largeur (BFS) :
  - Explore l’espace de recherche niveau par niveau.
  - Garantie le chemin le plus court mais peut être gourmand en mémoire.
  - Implémenté en utilisant une file d’attente.
- Recherche en profondeur (DFS) :
  - Explore aussi profondément que possible le long de chaque branche avant de revenir en arrière.
  - Moins gourmand en mémoire mais peut ne pas trouver le chemin le plus court.
  - Implémenté en utilisant une pile.
Implémentation de la recherche non informée :
- Utilisé le 8-Puzzle comme problème d’exemple.
- Représenté les états comme des listes de chiffres, avec 0 comme tuile vide.
- Démontré les implémentations de BFS et DFS en Python.
- Montré que BFS a trouvé la solution optimale en plus d’itérations, tandis que DFS a trouvé une solution sous-optimale plus rapidement.
Limites de la recherche non informée :
- Inefficace pour les problèmes grands ou complexes en raison de sa nature exhaustive.
- Manque de connaissance du domaine conduit à une exploration inutile.

Prochaine conférence

Nous explorerons plus en détail les fonctions heuristiques et examinerons d’autres algorithmes de recherche.

Références

Russell, Stuart, et Peter Norvig. 2020. Artificial Intelligence: A Modern Approach. 4ᵉ éd. Pearson. http://aima.cs.berkeley.edu/.

Schrittwieser, Julian, Ioannis Antonoglou, Thomas Hubert, Karen Simonyan, Laurent Sifre, Simon Schmitt, Arthur Guez, et al. 2020. « Mastering Atari, Go, chess and shogi by planning with a learned model ». Nature 588 (7839): 604‑9. https://doi.org/10.1038/s41586-020-03051-4.

Silver, David, Aja Huang, Chris J. Maddison, Arthur Guez, Laurent Sifre, George van den Driessche, Julian Schrittwieser, et al. 2016. « Mastering the game of Go with deep neural networks and tree search ». Nature 529 (7587): 484‑89. https://doi.org/10.1038/nature16961.

Simon, Nisha, et Christian Muise. 2024. « Want To Choose Your Own Adventure? Then First Make a Plan. » Proceedings of the Canadian Conference on Artificial Intelligence.

Marcel Turcotte

[email protected]

École de science informatique et de génie électrique (SIGE)

Université d’Ottawa